1,为什么最小均方差是最优的
卡尔曼滤波本质上是寻找两个分布线性组合取得最新小均方差的问题。然后扩展到多维向量空间。
那么思考一下问什么当两个分布取得最小均方差的时候最优?
首先我先说明一下, 最小均方差并不是最优,而是很优。因为本质上是无法确定那种最优 。
所以为了工程上的可行我们通常是综合两个不同的测量数据,或者多一些也就四五个。那么这个时候求两个数据的均值是最优的吗?当然不是,以电子枪和水银温度计来说,通常水银温度计的测量更加准确,电子枪的测量误很大,所以如果我们求平均值的时候电子枪测量结果对最终预测的结果影响权重太大了,显然不合适。那么究竟怎么的比例合适?

我们要寻找最优的K,为什么可以用方差呢?方差是不是最优呢?我们说贫富差距大,实际就是因为方差很大,但是如何评价两个国家哪个国家的贫富差距更大呢?仅仅用方差可以吗?显然是不行的,比如两个国家一个是富人和穷人都很多,计算一个方差,但是另外一个国家富人只有几个,除此之外其他的人都很平均,但是计算出来的方差更大,那么我们能认为第二个国家贫富差距更大吗?显然不行。 尽管没有最理想的模型,但是方差确实是可以在一定程度上说明贫富差距,能一定程度说明围绕期望波动的剧烈程度 。那么这样我们当然可以将寻找方差最小作为不错的估计结果, 所以我们也可以定义这样的结果是按照方差大小来分布的最优 。
2,卡尔曼滤波扩展和数学本质

这个K值就和过程控制迭代中提到的卡尔曼增益成比例 ,
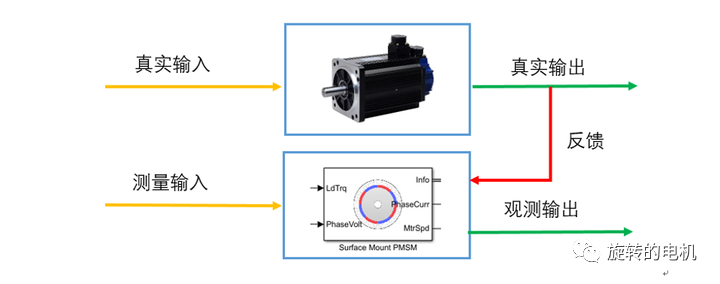
过程控制中的计算是卡尔曼滤波思想的应用。因为迭代以及多维空间导致很难理解 。
之所以我们看到的卡尔曼滤波很复杂是因为是用于过程控制迭代加上向量计算掩盖了本质,导致难以理解

3,卡尔曼滤波和互补滤波
还是以测温为例子,假设水银温度计的精度高,测温枪的精度低。在一个测量过程中,我如果是卡尔曼滤波我们要不断的计算卡尔曼增益,显然这个效率精度更好,但是许多时候计算量大一点。如果我们并不要求特别高的精度,我们就可以用下面的互补滤波来预测。互补滤波本质上就是固定卡尔曼滤波系数的简化版本,每一次迭代的卡尔曼滤波系数都不变。

许多精度要求不高环境比较稳定的情况下,互补滤波就可以满足使用
-
滤波器
+关注
关注
161文章
7805浏览量
178065 -
卡尔曼滤波
+关注
关注
3文章
165浏览量
24650
发布评论请先 登录
相关推荐
卡尔曼滤波的变种有哪些?1
卡尔曼滤波的变种有哪些?2
卡尔曼滤波的变种有哪些?3
卡尔曼滤波的变种有哪些?4
基于扩展卡尔曼滤波的机动目标航迹跟踪
卡尔曼滤波(KF)与扩展卡尔曼(EKF)
基于扩展卡尔曼滤波EKF的无感控制+Matlab/Simulink仿真案例




 卡尔曼滤波的总结和思维扩展
卡尔曼滤波的总结和思维扩展
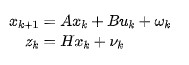










评论