当下,在数字音频世界中,基于快速傅里叶变换(FFT)和时间延时谱(TDS)功能的音频分析仪能够很轻松地揭示扬声器的振幅响应和相位响应。这些软件分析仪并不昂贵,被广泛应用于现场扩声、固定安装和扬声器的研发当中。其中耳熟能详的软件包括ARTA、Smaart、Systune和EASERA等等。
相位响应是一个常被提及的话题。很多从业者都会使用软件中的延时捕捉器、自动延时捕捉或相位补偿等相关功能来检查相位响应。尽管如此,他们当中的大多数人并不了解这一功能背后的基本原理。本文面向具有扬声器测量经验的读者,讨论如何设置一个正确的时间参考值以便解读相位响应。
1 有关相位响应的基本原理
1.1脉冲响应与数字音频
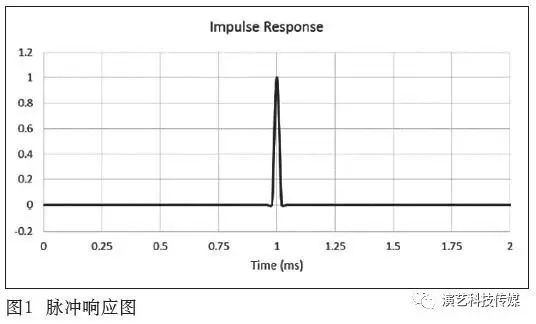
首先讨论一下脉冲响应图,如图1所示,它展示了一个理想状态下的脉冲响应(狄拉克脉冲),其峰值出现在1 ms。这个时域图所显示的信息包括:
- 一个脉冲能量出现在1 ms时间点上;
- 该信号的传输延时为1 ms;
- Y轴上的数值为1,意味着信号振幅为+1。
仔细分析图1就能发现,脉冲响应的起始点早于1 ms。随之而来的问题是,信号到达的实际时间的确略早于1 ms吗?
如果将脉冲响应曲线通过点与点相连接构成,则有助于进行视觉化观察。当图1仅通过图像点标记数值时,则变成图2所示的状态,能够清楚地看到,脉冲仅仅包含一个恰好在1 ms时到达的能量尖峰。理解脉冲响应从何处开始是读取相位响应的第一步。并非所有分析仪都能够显示图像点,但了解数字设备中的曲线如何形成是非常重要的。

注意,在数字域中,所有的数值都是离散的(非连续的),图表的精度由采样率决定。一个狄拉克脉冲仅包含一个采样。
1.2传输延时和相位响应
为什么需要考虑脉冲的起始点?先来验证一下传输延时对于相位响应的影响。传输延时可能由如下因素导致。
(1)声音传播时间
声音传播时间指的是直达声到达传声器需要的时间。声音在空气中约以344 m/s(20 ℃)的速度传播。了解声音在空气中的传播需要时间是十分重要的。
(2)处理延时
数字信号处理、数/模转换和模/数转换通常需要一定的处理时间。一个数字扬声器管理系统的模/数和数/模转换所产生的延迟通常约为2 ms。如果处理工作繁重,那么处理器会需要更长的处理时间,信号传输延时也会相应增加。
1.3有限脉冲响应滤波器
使用有限脉冲响应线性相位滤波器可能导致传输延时的增加。针对不同的应用场合,滤波器所带来的处理延时可能小到1 ms,也可能大于500 ms。在图3中,假设通过双通道快速傅里叶变换对一个“完美”的扬声器进行测量,获得的脉冲响应为图中的蓝色脉冲,可以观察到一个0.5 ms的传输延时(假设“完美”的测试传声器距离扬声器大约17 cm)。黑色脉冲显示的是将传输延时去除后,脉冲峰值恰好位于0 ms时的情况。这一结果是通过将脉冲响应做周期性移动来获得的(后文将会对此进行解释)。红色脉冲表示传输延时被多去除了0.5 ms时的情况。红色脉冲是一个非因果关系的响应,即输出并非由输入所导致。位于0 ms之前的脉冲可以被认为是输入信号进入系统之前所得到的输出。
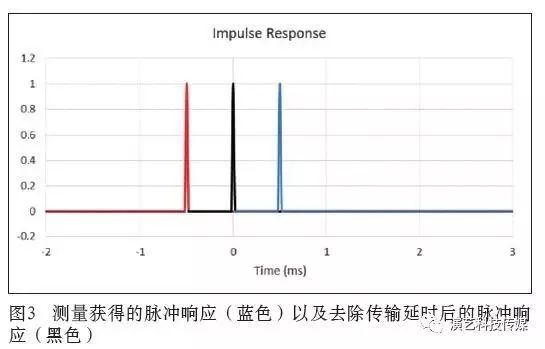
图4显示了当传输延时被正确去除后扬声器系统的相位响应,此时脉冲的峰值位于0 ms。请注意相位响应在0°时为平坦的,群延时也同样为0°。
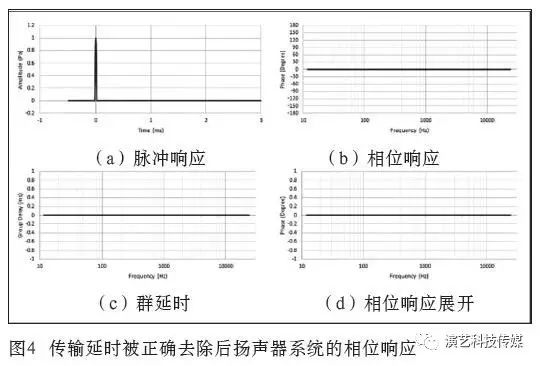
群延时是相位曲线斜率的负值。群延时可由如下公式表示:
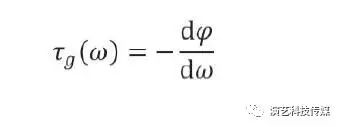
其中,ω 是角频率或频率乘以2π; φ 为相位;τ为群延时。
图5是0.5 ms传输延时没有被去除时扬声器的相位响应,为了更清楚地观察相位响应,图5(d)显示了经过放大后的未折叠部分的相位响应。

通过公式1=T×f(T为周期,单位为s;f为频率,单位为Hz),可以算出0.5 ms是2 000 Hz的一个周期。声波的周期是其运动360°所需要的时间。因此,2 000 Hz的相位为-360°(相位角为负值意味着该频率的相位滞后)。对于1 000 Hz来说,它需要1 ms来完成一个周期,因此它所呈现的相位为-180°。换句话说,在0.5 ms传输延时存在的情况下,1 000 Hz被拖慢了半个周期,而2 000 Hz被拖慢了一个周期。在没有去除传输延时的情况下,输入信号所有的频率分量都被移动了同样的时间量。这并不是相位失真。如果把图5中的X轴(频率轴)从对数刻度变为线性刻度,则能够看到一条直线,如图6所示。注意:相位角为负值意味着该频率的相位滞后。

从图5(d)中还能够观察到群延时,对应0.5 ms的传输延时。当脉冲被过量移动0.5 ms时会发生什么,图8中将图5(0.5 ms传输延时-蓝色曲线)和图7(过量移除0.5 ms传输延时-红色曲线)中的相位响应叠放在一起,可以观察到相位响应的不同方向。过量移除传输延时会导致正相位和负群延时数值。
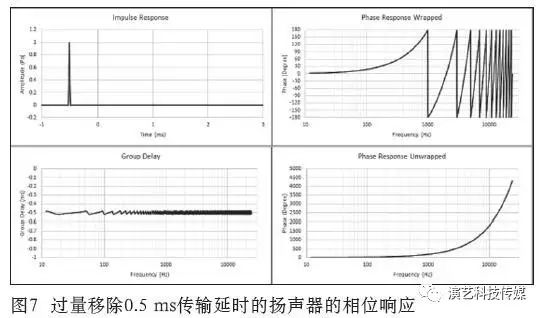

即便是很小的传输延时,也会对高频的相位响应曲线产生极大的影响,理解这一点非常重要。
2 相位响应的正确解读及传输延时的移除
2.1移除传输延时
由于传输延时会导致一个线性的相位偏移,因此,能够很容易被预测和计算。移除传输延时的常用方法是对信号做周期性移动,使脉冲响应的峰值处在0 ms。这一功能在测量软件中通常是以自动延时查找(Auto Delay Finder)、自动峰值查找(Auto Peak Finder)、最大峰值归零(Nomalize Max to Zero)等来命名。但是,这种方式对于相位响应的读取可能产生误导,比如,在使用了低通滤波器导致1 000 Hz以上的能量较弱时。
不同的软件所采用的去除传输延时的方法不同(见图9-图11)。有些软件配备了直接将脉冲峰值对齐到0 ms的功能,而其他软件则需要手动设置光标的位置。光标的位置将会定义一个向左的矩形窗口或者截止位置。

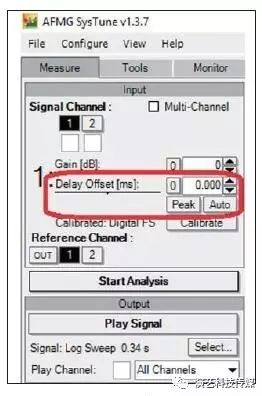
图10 Systune通过手动输入延时量或“峰值”按钮去除传输延

需要记住的是,扬声器的脉冲响应开始于声音到达测试传声器的那一刻。脉冲响应的峰值与到达传声器的初始峰值并不总是完全一致,了解这一点十分重要。使用脉冲响应的峰值作为参考点可能会误导对相位响应的理解与计算。
2.2最小相位(Minimum Phase)简介
最小相位指振幅响应和相位响应之间的关系可以相互预测,振幅响应的改变会带来相位响应的改变,这种关系可以通过希尔伯特变换来进行计算。图12呈现了振幅响应及相对应的最小相位响应的关系。
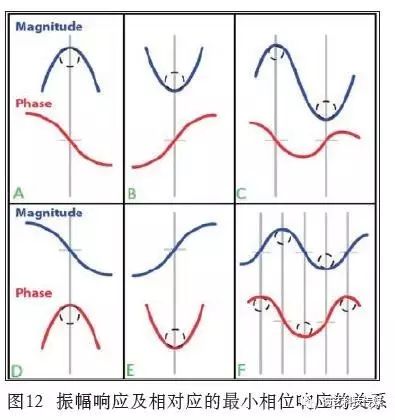
多数扬声器系统并不是最小相位系统,但多数扬声器单元则是最小相位系统。最小相位系统的另一个例子是无限脉冲响应滤波器,但全通滤波器除外。
当相位数值为正,意味着该频率的相位提前。在一个最小相位系统当中,如果频率响应(从低频到高频)呈上升趋势,相位数值为正。比如,给一个扬声器单元加上高通滤波器,在滤波器的衰减量从最大到0(不衰减)的频率范围内,这个扬声器单元通常会出现这种情况。另一个例子是使用低通滤波器的情况,在滤波器的衰减量从0(不衰减)到最大的频率范围内,频率响应(从低频到高频)呈下降趋势,在最小相位系统中,这会导致相位数值为负(相位落后)。
图13中所描述的一个无分频网络的扬声器经过IIR滤波器处理后的响应曲线。其中高通滤波器的截止频率为60 Hz,低通滤波器的截止频率为12 500 Hz。通过观察可以发现:

- 在低频区(低于200 Hz),因为高通滤波器的作用(频率响应呈上升趋势),相位数值为正;
- 在高频区(高于8 000 Hz),因为低通滤波器的作用(频率响应呈下降趋势),相位数值为负;
- 在1 000 Hz附近,相位数值接近于0。这是由于中频段没有频率响应上的改变所导致的结果。
从图13中还会发现脉冲的峰值稍稍错开,位于0 ms的右侧,以图像点方式描绘的脉冲响应的情况见图14,可以看出,初始到达的脉冲信号被准确地对齐在0 ms上。

大多数分析仪并不具备将连续曲线转化为图像点的功能,因此,同时对频域的传递函数(振幅响应和相位响应)和时域的脉冲响应进行观察是十分重要的。而当使用自动延时查找功能时会出现什么情况?通过观察图15发现:

- 在对脉冲响应做周期性移动时,频率响应不会有任何变化;
- 脉冲响应峰值被移动至0 ms;
- 相位响应变得更加平坦,但请注意其数值在10000 Hz之前为正值。相位数值为正,尤其在已知中频段频率响应平坦,高频段(8 000 Hz以上)频率响应下降的情况下,不难判断出脉冲响应略微地被过度移动了。
图16中给出一个数值为正的相位响应的例子,一个2 in扬声器单元被安装在封闭的小箱体中,测试传声器其距离1 m。该测量在没有任何电子滤波器介入的情况下进行,是一个最小相位系统。通过图16可以得到以下结果:

- 红色虚线是在ARTA中根据振幅响应计算出的最小相位曲线,其结果和实际测量的相位曲线(黑色实线)基本重合,意味着从测量数据中移除的传输延时量是正确的;
- 相位的数值一直到20000 Hz都为正数,这是由于振幅响应一直在上升所导致。
图17为图16和图12的对比,请注意两个绿色矩形区域:在200 Hz以下,频率响应是上升的,因此如图12A所示,相位响应开始呈现正值;在高频区间,10000 Hz附近,测量值及计算值与图12C是如何相匹配的。
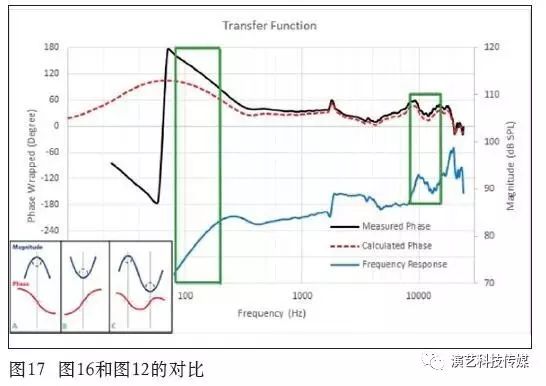
通过对脉冲响应的周期性移动,可以很容易地改变相位响应,或是找到相位响应最为平坦的位置。但是,在实际工作中还必须思考一个问题:得到的相位响应是否有意义?
2.3相位响应的正确解读
在本文中,“正确解读”是指找到对于工程应用来说有价值的相位响应。请看图18中的两组来自于相同的测量文件的相位响应曲线:

- 红色曲线看上去是更好看(更平坦)的相位响应曲线;
- 黑色曲线有很多弯折,尤其在1 000 Hz以上;
- 黑色曲线对于传输延时进行了正确的去除,红色曲线是将脉冲峰值放置在0 ms所得到的结果(使用自动延时查找功能),输入信号的极性被反转了。
有很多方法能够让相位响应看上去更加平坦,但这并不意味着平坦的曲线对于工程应用来说是有效的。所以,将会更多地针对黑色曲线进行讨论。
再讨论另一个相位响应的例子以进行对照。图19是一只12 in的两分频号筒式扬声器的两套测量数据,黑色曲线的测量方式是:使用扬声器内部的interwetten与威廉的赔率体系 分频电路(无源分频器),没有DSP介入,只需要一个功率放大器进行驱动;红色曲线的测量方法是:通过DSP对高音单元和低音单元做分频处理(有源分频器),每个单元各需要一个功放进行驱动。

当正确地移除了脉冲响应的传输延时后,就能够对曲线进行正确的解读。以下观察和讨论仅集中在与相位相关的话题上。
(1)计算得到的最小相位响应与实际测量得到的相位响应不同
这个情况是正常的。因为这只两分频扬声器无论是使用无源分频还是有源分频,它都不是一个最小相位系统。单个的扬声器单元有可能是最小相位系统,但高音单元和低音单元放在一起作为一个扬声器系统,分频器的引入就破坏了它是最小相位系统的可能性,自然也无法通过频率响应来计算相位响应。
(2)黑色曲线在高频区间明显的相位跌落/翻折,尤其在1000 Hz以上
黑色曲线是扬声器使用无源分频器时测得的。如果观察脉冲响应,可以发现在脉冲峰值之前有一个小的起伏,应该是低音单元的脉冲,它弱于较高的脉冲峰尖,这是因为脉冲响应中的高频能量占了主导;当对低音单元施加一个低通滤波器时(截止频率低于2 000 Hz),脉冲的高度将会被显著地减弱。较高的脉冲峰值应该是高音单元,它到达测试传声器的时间较晚(大约晚到0.7 ms)。
由于扬声器使用了无源分频器,能够推测:高音单元的音圈相比低音单元的音圈在位置上较为靠后,这通常是由于高频号筒的深度所导致的;来自低音单元的直达声首先到达传声器,高音单元的声音在0.7 ms之后到达。正如之前针对图5的讨论,相比低音单元最先到达,高音单元滞后所带来的额外的传输延时导致了高频相位的跌落/翻折以及较高的群延时数值(随后即将讨论)。
(1)黑色曲线中高频段(1 000 Hz以上)具有较高的群延时数值
接着之前的讨论,由于高音单元和低音单元之间的到达时间存在差异,可以在1000 Hz以上的频率观察到约为0.7 ms的正数群延时。这清楚地说明了高频单元比低频单元晚到0.7 ms。
红色的群延时曲线在1 000 Hz以上的数值为0 ms。通过将红色和黑色的群延时曲线以及脉冲响应图进行对比,可以推测:在红色曲线的测量过程中,DSP不仅做了有源分频,还特意给低音单元额外加了一点延时,调整了高低音单元直达声到达时间差的问题。
(2)红色群延时曲线在低频(低于100 Hz)的群延时数值更高
如果留意频率响应,红色曲线的振幅要比黑色曲线更高。这意味着DSP除了做分频,调整扬声器单元的时间差,还在低音单元的65 Hz左右进行了少量增益提升。
这个参量均衡的介入会增加群延时。再看图18的红色曲线,在将这只无源扬声器的脉冲响应峰值移动至0 ms后,看到的相位响应变得更加平坦,然而这条平坦的相位曲线对于工程应用来说并无意义,它甚至将输入信号的极性都反转了。也许它在营销领域能发挥些作用吧。
3 结语
本文讨论的结论可以归为一句话:通过正确的判断和移除传输延时,才能获得对工程应用有价值的相位响应。
-
功率放大器
+关注
关注
102文章
3590浏览量
131959 -
分频器
+关注
关注
43文章
447浏览量
49965 -
IIR滤波器
+关注
关注
0文章
31浏览量
11543 -
傅里叶变换
+关注
关注
6文章
442浏览量
42617 -
TDS
+关注
关注
0文章
14浏览量
14400
发布评论请先 登录
相关推荐
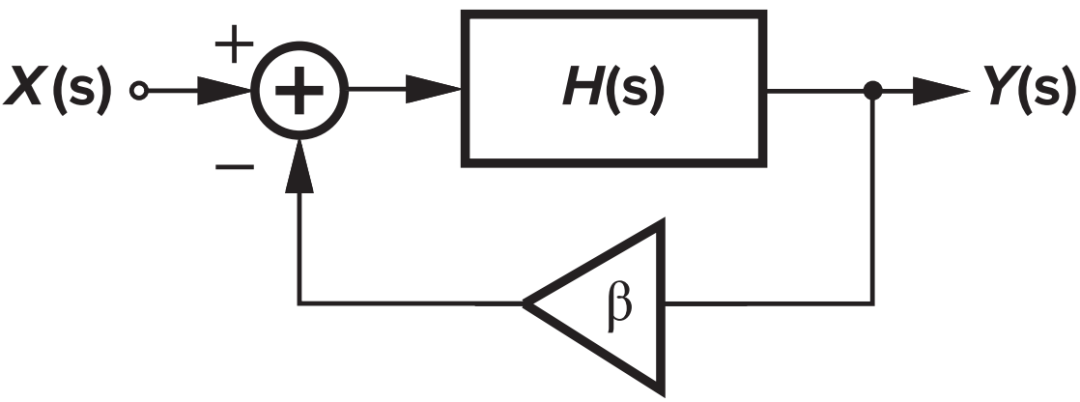
开环响应、环路响应、闭环响应与相位裕度关系浅析
什么是液晶电视可视角度
如何得到与观察PID响应曲线
有源滤波器相位响应
请问一下运放单位增益响应曲线是否正常?能用不?
什么是可视角度
运放相位裕度的认识与理解

针对幅度响应设计的有源滤波器的相位响应介绍

频率响应曲线增益案例摘要
理解脱扣曲线
有源滤波器中的相位响应





 从不同的视角理解相位响应曲线
从不同的视角理解相位响应曲线










评论