模拟集成电路设计-基本π网络（上）

基本π网络是interwetten与威廉的赔率体系 放大器的基础，大部分放大器或者类放大器电路都有基本π网络的身影，新的放大器结构也是对基本π网络延伸和改良。所以学好基本π网络是非常重要的，深刻理解基本π网络后，阅读更复杂的放大器的文献就不是问题了。

基本π网络结构

基本π网络通过在互易π 网络一侧添加一个压控电流源（VCCS）形成一个非互易网络。我们对这个π网络做节点分析（大家可以顺便想一下节点分析和Y参数的关系）：

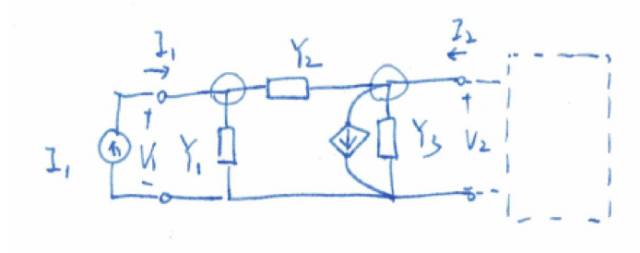
大家看，在等式右侧的受控电流移到等式左边之前，Y矩阵还是对称的（互易）。

受控电流源移动到左侧之后，正式的Y矩阵就不再对称了（网络不再互易）。换句话说，VCCS打破了这个电路的互易性。

我们假设端口2是开路。然后可以解出这个二端口网络的一个最常用的传输函数，即跨阻。

强行解矩阵谁都会，用克莱姆法则，我们可以算出V 2 /I 1 ：

这个表达式是高熵的，对设计不友好的。

Prof. Abidi教育我们，要把传输函数写成规整的、对设计友好的形式，这样才不会成为划水的电路设计师：

这三种公式都是低熵的，因为他们遵循了一个基本型：

这个基本型是Prof. Abidi 原引Prof. Middlebrook 的广义反馈定理（General Feedback Theorem），以后有机会我可以专门讲Middlebrook的双重抵消注入（Null Double Injection）和广义反馈定理。这里先简单介绍一下上面的这个基本型。

H ∞ 是理想闭环增益，它可以有单位，当有单位时，“增益”这个词不再准确，但是大家心里明白就行。

T是回路增益，它不可以有单位。T与这个网络反馈的能力相关。

Tn是Null 回路增益，它也不可以有单位。Tn与这个网络的前馈的能力相关。

想要达到理想闭环增益，T和Tn都必须远大于1才行。

用基本π网络分析实际电路

基本π网络在很多地方都有应用：

例1：电阻负载跨导放大器（OTA）

用基本型分析电路，算出增益为：

大家看，-R 2 /R1是我们通常会假设一个理想运放接反馈电阻会有的增益。但是，要想用OTA达到同样的理想增益，我们需要

然后重写增益函数的分母，我们可以得到：

所以还要：

这里A是理想增益幅度R 2 /R1

满足了这三点，我们才能有理想的增益。这说明，如果源阻抗比较小，那gm就会要很大，导致更高的功耗。满足了第二点，第一点一般都可以满足，因为需要增益的话R2一般比R1要大。但是第三点要求我们的负载阻抗不能太小，因为它要除以一个增益乘以gm后还要远大于1。

例2：光电信号放大器

下图展示了一个简单的光电信号放大器，该电路用于测量光电二极管输出的电流信号并转换为电压输出。

该电路的等效模型如下，C1主要为光电二极管的电容，C3为VCCS的寄生电容和负载电容（下一级的输入电容）。我们可以猜测C3的一半是实现gm时产生的寄生电容一半是负载电容。因为要捕捉微弱的光线，光电二极管一般很大，所以C1可以被假设远大于C 3 。R2为反馈电阻。

现在根据基本π型列出传输函数，并重写成二阶低通基本型：

光电信号是基带信号，带宽很高，所以我们放大器的-3dB带宽要达到信号的带宽。所以我们要让Q等于1，这样带宽约为ω 0 ，而且尖峰非常小（阶跃响应不会有波纹）。

我们又知道C3远小于C 1 。所以

如果设计满足公式1，那么gmR2也就远大于1了，因为C 1 /C3远大于1。

ω0根据信号带宽已经定下，R2根据光电二极管电流大小和目标输出幅度可以定下，C1根据发光二极管的尺寸已经定下，所以我们只需要选择gm和C 3 。之后我们会学习MOSFET结构，但是现在我们可以做一个简单的预习设计。根据ω0和C1我们可以算出g m ，在我们所假设的一种特定条件下，gm正比于W/L。然后，根据ω0和R2我们可以算出C 3 ，它正比于W×L。知道了W/L和W×L我们就可以算出W和L了，如果算出的L小于你所用工艺的L，那么这个结构就不能满足你的需求啦，要么换一个结构要么换更好的工艺吧！

最后做出来的传输函数应该长这样：

最后说一点很重要，任何手算的设计数据都是估计值，用仿真机跑出来后肯定有比较大的误差，但是没关系，我们可以降低估算的尺度，再设计几次，或者用仿真机微调。但是不管做任何设计，盲目地使用仿真机都是错误的，从手算开始的习惯是非常重要的。