什么是电子产品中的透明电池或结构

什么是电子产品中的透明电池或结构？我们大多数人，尤其是我们参与数据转换器的同事，在处理此类对象时没有注意到它们的透明字符。最好的例子是在许多ADC和DAC中发现的著名的R-2R梯形图。R-2R是如何建造的，还有其他类似的电路吗？

关于结构的透明特性

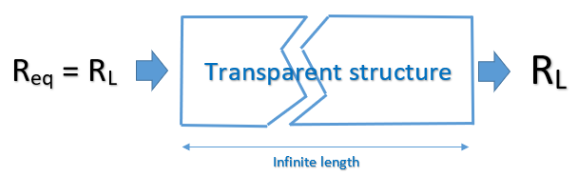
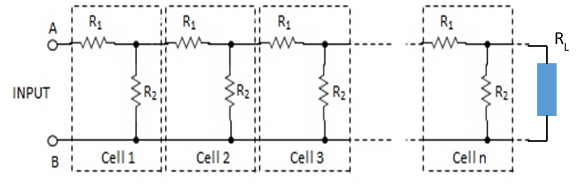
什么是“透明”细胞？它是一个结构，就像干净的玻璃一样，你可以透过它看而不会有任何扭曲。“玻璃”厚度可以是无限的，如上图所示！在电子产品中，透明特性是从源头通过结构看到的端接电阻RL。让我们在下图中著名的R-2R梯子中说明它。从左边看，即使细胞数量是无穷无尽的，也总是看到RL！但是，这可以不受任何限制（即RL值，细胞结构）吗？不幸的是没有。存在链接 RL 值和透明单元格的条件。

为什么透明单元格很重要？

尽管讨论可能非常理论化，但有一个非常著名的透明结构称为R-2R梯子。它具有非常有用的特性，例如能够产生用于DAC和ADC的二进制供电电压。稍后会详细介绍。R-2R梯形图的特点是什么？让我们更详细地了解R-2R梯形图的结构：通过放置R1 = R，R2 = 2R并以RL= 2R终止，您可以获得具有非常有趣和显着特性的电路，例如：

输入看到的相同 RL 与单元格数量无关;因此，它可以是无限的）;整个R-2R结构实际上是“透明的”！

输入端始终看到一个相同的等效阻抗2R，与串联中的电池数量无关。

如果在输入端施加电压 E，则节点上的电压显示为 E/2、E/4、E/8 等。使其成为二进制DAC结构的理想选择。

如何找到其他透明单元格？

要回答这个问题，请参阅下面的基本电池结构 R1-R2 并由 RL 终止：

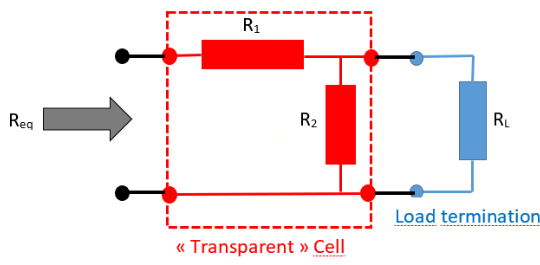
当从左侧看到的总等效电阻（Req）等于RL时，R1和R2制成的电池（红色）可以称为“透明”电池。在这种情况下，您可以根据需要堆叠（即串联）任意数量的红色单元格：Req 将看到相同的负载电阻 RL！这仅在链接 R1、R2 和 RL 的特定条件下发生。为了确定条件，让我们写出从输入中看到的等效电阻。可以观察到RL与R2并联，然后与R1串联。

Req = R2*RL/（R2+RL） + R1，这必须再次等于RL。从输入到RL具有“透明度”的一般等式（和条件）为：

R2*RL/（R2+RL） + R1 = RL

通过排列项：RL² - R1RL – R1R2 = 0，可以看作是一个二次方程，RL为未知。通过求解：RL = R1/2 +/- （R1² +4R1R2）1/2/2 ：其中只能考虑正解：

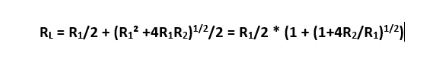
当 R1、R2 和 RL 如上所述链接时，您将获得一个“透明”单元格！而且有无数的解决方案！让我们在我们著名的 R-2R 阶梯上验证一下，R1=R 和 R2=2R，RL 等于 2R

透明电池的其他（R-2R除外）实际示例：

当 R1=R 和 R2=12R 时，我们的 RL 等于 4R。

当R1=R和R2=3R时，RL必须等于2.303*R才能获得透明特性！

扭转问题：

找到带有RL修复的R1和R2，可以以不同的方式解决问题。修复 RL 并计算 R1 和 R2。

让我们从连接 R1、R2 和 RL 的第一个方程重新开始：

RL² - R1RL– R1R2= 0

现在让我们把 R2= kR1k只是一个比率

然后我们有RL² - R1RL– kR1² = 0

通过重命名 R1= R 我们简单地得到：RL²- RRL– kR² = 0

通过将上述二阶方程重新排列为未知：kR² + RLR - RL²= 0

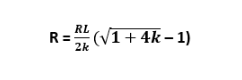
结论

我们已经解释了R-2R梯子是如何建造的，以及它给我们带来的有用特性。我们还建立了一个数学工具来寻找其他类似的结构。这些工具和公式允许读者走得更远，找到电路电缆，例如，给出电压系列，如 E、E/3、E/9 等。这是为了构建不同类型的DAC

审核编辑：郭婷