广大码农同学们大多都有个共识,认为算法是个硬骨头,很难啃,悲剧的是啃完了还未必有用——除了面试的时候。实际工程中一般都是用现成的模块,一般只需了解算法的目的和时空复杂度即可。
不过话说回来,面试的时候面算法,包括面项目中几乎不大可能用到的算法,其实并不能说是毫无道理的。算法往往是对学习和理解能力的一块试金石,难的都能掌握,往往容易的事情不在话下。志于高者得于中。反之则不成立。另一方面,虽说教科书算法大多数都是那些即便用到也是直接拿模块用的,但不幸的是,我们这群搬砖头的有时候还非得做些发明家的事情:要么是得把算法当白盒加以改进以满足手头的特定需求;要么干脆就是要发明轮子。所以,虽说面试的算法本身未必用得到,但熟悉各种算法的人通常更可能熟悉算法的思想,从而更可能具备这里说的两种能力。
那么,为什么说算法很难呢?这个问题只有两种可能的原因:
算法本身就很难。也就是说,算法这个东西对于人类的大脑来说本身就是个困难的事儿。
讲得太烂。
下面会说明,算法之所以被绝大多数人认为很难,以上两个原因兼具。
我们说算法难的时候,有两种情况:一种是学算法难。第二种是设计算法难。对于前者,大多数人(至少我当年如此)学习算法几乎是在背算法,就跟背菜谱似的(“Cookbook”是深受广大码农喜爱的一类书),然而算法和菜谱的区别在于,算法包含的细节复杂度是菜谱的无数倍,算法的问题描述千变万化,逻辑过程百转千回,往往看得人愁肠百结,而相较之下任何菜谱涉及到的基本元素也就那么些(所以程序员肯定都具有成为好厨师的潜力:D)注意,即便你看了算法的证明,某种程度上还是“背”(为什么这么说,后面会详述)。我自己遇到新算法基本是会看证明的,但是发现没多久还是会忘掉,这是死记硬背的标准症状。如果你也啃过算法书,我相信很大可能性你会有同感:为什么当时明明懂了,但没多久就忘掉了呢?为什么当时明明非常理解其证明,但没过多久想要自己去证明时却发现怎么都没法补上证明中缺失的一环呢?
初中学习几何证明的时候,你会不会傻到去背一个定理的证明?不会。你只会背结论。为什么?一方面,因为证明过程包含大量的细节。另一方面,证明的过程环环相扣,往往只需要注意其中关键的一两步,便能够自行推导出来。算法逻辑描述就好比定理,算法的证明的过程就好比定理的证明过程。但不幸的是,与数学里面大量简洁的基本结论不同,算法这个“结论”可不是那么好背的,许多时候,算法本身的逻辑就几乎包含了与其证明过程等同的信息量,甚至算法逻辑本身就是证明过程(随便翻开一本经典的算法书,看几个经典的教科书算法,你会发现算法逻辑和算法证明的联系有多紧密)。于是我们又回到刚才那个问题:你会去背数学证明么?既然没人会傻到去背整个证明,又为什么要生硬地去背算法呢?
那么,不背就不背,去理解算法的证明如何?理解了算法的证明过程,便更有可能记住算法的逻辑细节,理解记忆嘛。然而,仍然不幸的是,绝大多数算法书在这方面做的实在糟糕,证明倒是给全了,逻辑也倒是挺严谨的,可是似乎没有作者能真正还原算法发明者本身如何得到算法以及算法证明的思维过程,按理说,证明的过程应该反映了这个思维过程,但是在下文关于霍夫曼编码的例子中你会看到,其实饱受赞誉的CLRS和《Algorithms》不仅没能还原这个过程,反而掩盖了这个过程。
必须说明的是,没有哪位作者是故意这样做的,但任何人在讲解一个自己已经理解了的东西的时候,往往会无意识地对自己的讲解进行“线性化”,例如证明题,如果你回忆一下高中做平面几何证明题的经历,就会意识到,其实证明的过程是一个充满了试错,联想,反推,特例,修改问题条件,穷举等等一干“非线性”思维的,混乱不堪的过程,而并不像写在课本上那样——引理1,引理2,定理1,定理2,一口气直到最终结论。这样的证明过程也许容易理解,但绝对不容易记忆。过几天你就会忘记其中一个或几个引理,其中的一步或几步关键的手法,然后当你想要回过头来自己试着去证明的时候,就会发现卡在某个关键的地方,为什么会这样?因为证明当中并没有告诉你为什么作者当时会想到证明算法需要那么一个引理或手法,所以,虽说看完证明之后,对算法这个结论而言你是知其所以然了,但对于算法的证明过程你却还没知其所以然。在我们大脑的记忆系统当中,新的知识必须要和既有的知识建立联系,才容易被回忆起来(《如何有效地学习与记忆》),联系越多,越容易回忆,而一个天外飞仙似地引理,和我们既有的知识没有半毛钱联系,没娘的孩子没人疼,自然容易被遗忘。(为什么还原思维过程如此困难呢?我曾经在知其所以然(一)里详述)
正因为绝大多数算法书上悲剧的算法证明过程,很多人发现证明本身也不好记,于是宁可选择直接记结论。当年我在数学系,考试会考证明过程,但似乎计算机系的考试考算法证明过程就是荒谬的?作为“工程”性质的程序设计,似乎更注重使用和结果。但是如果是你需要在项目中自己设计一个算法呢?这种时候最起码需要做的就是证明算法的正确性吧。我们面试的时候往往都会遇到一些算法设计问题,我总是会让应聘者去证明算法的正确性,因为即便是一个“看上去”正确的算法,真正需要证明起来往往发现并不是那么容易。
所以说,绝大多数算法书在作为培养算法设计者的角度来说是失败的,比数学教育更失败。大多数人学完了初中平面几何都会做证明题(数学书不会要求你记住几何所有的定理),但很多人看完了一本算法书还是一团浆糊,不会证明一些起码的算法,我们背了一坨又一坨结论,非但这些结论许多根本用不上,就连用上的那些也不会证明。为什么会出现这样的差异?因为数学教育的理想目的是为了让你成为能够发现新定理的科学家,而码农系的算法教育的目的却更现实,是为了让你成为能够使用算法做事情的工程师。然而,事情真的如此简单么?如果真是这样的话干脆连算法结论都不要背了,只要知道算法做的是什么事情,时空复杂度各是多少即可。
如果说以上提到的算法难度(讲解和记忆的难度)属于Accidental Complexity的话,算法的另一个难处便是Essential Complexity了:算法设计。还是拿数学证明来类比(如果你看过《Introduction to Algorithms:A Creative Approach》就知道算法和数学证明是多么类似。),与单单只需证明相比,设计算法的难处在于,定理和证明都需要你去探索,尤其是前者——你需要去自行发现关键的那(几)个定理,跟证明已知结论相比(已经确定知道结论是正确的了,你只需要用逻辑来连接结论和条件),这件事情的复杂度往往又难上一个数量级。
一个有趣的事实是,算法的探索过程往往蕴含算法的证明过程,理想的算法书应该通过还原算法的探索过程,从而让读者不仅能够自行推导出证明过程,同时还能够具备探索新算法的能力。之所以这么说,皆因为我是个懒人,懒人总梦想学点东西能够实现以下两个目的:
一劳永逸:程序员都知道“一次编写到处运行”的好处,多省事啊。学了就忘,忘了又得学,翻来覆去浪费生命。为什么不能看了一遍就再也不会忘掉呢?到底是教的不好,还是学得不好?
事半功倍:事实上,程序员不仅讲究一次编写到处运行,更讲究“一次编写到处使用”(也就是俗称的“复用”)。如果学一个算法所得到的经验可以到处使用,学一当十,推而广之,时间的利用效率便会大大提高。究竟怎样学习,才能够使得经验的外推(extrapolate)效率达到最大呢?
想要做到这两点就必须尽量从知识树的“根节点”入手,虽然这是一个美梦,例如数学界寻找“根节点”的美梦由来已久(《跟波利亚学解题》的“一点历史”小节),但哥德尔一个证明就让美梦成了泡影(《永恒的金色对角线》));但是,这并不阻止我们去寻找更高层的节点——更具普适性的解题原则和方法。所以,理想的算法书或者算法讲解应该是从最具一般性的思维法则开始,顺理成章地推导出算法,这个过程应该尽量还原一个”普通人“思考的过程,而不是让人看了之后觉得”这怎么可能想到呢?
以本文上篇提到的霍夫曼编码为例,第一遍看霍夫曼编码的时候是在本科,只看了算法描述,觉得挺直观的,过了两年,忘了,因为不知道为什么要把两个节点的频率加在一起看做单个节点——一件事情不知道“为什么”就会记不牢,知道了“为什么”的话便给这件事情提供了必然性。不知道“为什么”这件事情便可此可彼,我们的大脑对于可此可彼的事情经常会弄混,它更容易记住有理有据的事情(从信息论的角度来说,一件必然的事情概率为1,信息量为0,而一件可此可彼的事情信息量则是大于0的)。第二遍看是在工作之后,终于知道要看证明了,拿出著名的《Algorithms》来看,边看边点头,觉得讲得真好,一看就理解了为什么要那样来构造最优编码树。可是没多久,又给忘了!这次忘了倒不是忘了要把两个节点的频率加起来算一个,而是忘了为什么要这么做,因为当时没有弄清霍夫曼为什么能够想到为什么应该那样来构造最优编码树。结果只知其一不知其二。
必须说明的是,如果只关心算法的结论(即算法逻辑),那么理解算法的证明就够了,光背算法逻辑难记住,理解了证明会容易记忆得多。但如果也想不忘算法的证明,那么不仅要理解证明,还要理解证明背后的思维,也就是为什么背后的为什么。后者一般很难在书和资料上找到,唯有自己多加揣摩。为什么要费这个神?只要不会忘记结论不就结了吗?取决于你想做什么,如果你想真正弄清算法设计背后的思想,不去揣摩算法原作者是怎么想出来的是不行的。
回到霍夫曼编码问题,我们首先看一看《Algorithms》上是怎么讲的:
首先它给出了一棵编码树的cost function:
cost of tree = Σ freq(i) * depth(i)
这个cost function很直白,就是把编码的定义复述了一遍。但是接下来就说了:
There is another way to write this cost function that is very helpful.Although we are only given frequencies for the leaves, we can define the frequency of any internal node to be the sum of the frequencies of its descendant leaves; this is, after all, the number of times the internal node is visited during encoding or decoding…
接着就按照这个思路把cost function转换了一下:
The cost of a tree is the sum of the frequencies of all leaves and internal nodes, except the root.
然后就开始得出算法逻辑了:
Thefirst formulationof the cost function tells us that thetwo symbols with the smallest frequencies must be at the bottom of the optimal tree, as children of the lowest internal node (this internal node has two children since the tree is full). Otherwise, swapping these two symbols with whatever is lowest in the tree would improve the encoding.
This suggests that we start constructing the tree greedily: find the two symbols with the smallest frequencies, say i and j, and make them children of a new node, which then has frequency fi + fj. To keep the notation simple, let’s just assume these are f1 and f2. By thesecond formulationof the cost function, any tree in which f1 and f2 are sibling-leaves has cost f1 + f2 plus the cost for a tree with n – 1 leaves of frequencies (f1 + f2), f3, f4, .., fn.The latter problem is just a smaller version of the one we started with.
读到这里我想大多数人有两种反应:
觉得理所当然。
觉得恍然大悟。
因为我当时也是这么觉得的。可是后来当我发现自己无法从头证明一遍的时候,我知道肯定是理解的不够深刻。如果理解的够深刻,那么基本上是不会忘掉的。
如果看完霍夫曼编码这样一个简短证明你觉得顺理成章,一切都挺显然,那就坏了,即便是看上去最基本的性质也往往实际上没那么显然。“逢山开路,遇水架桥”在我们今天看来是无比显然的事实,但是试想在没有桥的远古时代,一个原始人走到一条湍急的河流前,他会怎么想,他又能有什么法子呢?这是个他从来没有遇见过的问题。如果后来有一天,他路过另外一条小溪,看到小溪上有一截被闪电劈断的枯树,于是他踏着树干走过了小溪,并意识到“树横过河面”可以达到“过河”这个目的,这就将条件和目的建立了直接的联系(事实上,是自然界展示了这个联系,我们的原始人只是记住了这个联系)。后来他又路过那条河流,他寻思如何达到“过河”这个目的的时候,忽然意识到在他的记忆中已经遇到过需要达成同样目的的时候了,那个时候的条件是“树横过河面”,于是问题便归结为如何满足这个“树横过河面”的条件,而后一个问题就简单多了。(事实上波利亚在他的著作《How to Solve it》中举的正是这么个例子)
为什么那么多的算法书,就看不到有一本讲得好的?因为我们求解问题过程中的思维步骤太容易被自己当作“显然”的了,但除了我们天生就会的认知模式(联系,类比),没有什么是应该觉得显然的,试错是我们天生就会的思维法则么?是的,但是可供尝试的方案究竟又是怎么来的呢?就拿上面的例子来说,一个从没有见过枯树干架在小溪上的原始人,怎么知道用树架桥是一种可选的方案呢?俗话说巧妇难为无米之炊啊。我们大脑的神经系统会的是将目的和条件联系起来,第一次原始人遇到小溪过不去,大脑中留下了一个未实现的目的,后来见到小溪上的树干,忽然意识到树干是实现这个目的的条件,两者便联系起来了,因此问题就规约为如何架树干了。
回到《Algorithms》中的证明上,这个看似简洁明了的证明其实有几处非常不显然的地方,甚至不严谨的地方,这些地方也正是你过段时间之后试图自己证明的话会发现卡住的地方:
作者轻飘飘地就给出了cost function的另外一种关键的描述,而对于如何发现这种描述却只是一语带过:"There is another way to write this cost function that is very helpful..we can define the frequency of any internal node to be the sum of the frequencies of its descendant leaves“这其实就是我常常痛恨的“我们考虑…”,这里作者其实就是在说”让我们考虑下面这样一种奇妙的转换“,可是怎么来的却不说。但必须承认,《Algorithms》的作者还是算厚道的,因为后面他又稍微解释了一下:“this is, after all, the number of times the internal node is visited during encoding or decoding…”这个解释就有点让人恍然大悟了,但是千万别忘了,这种恍然大悟是一种错觉,你还是没明白为什么他会想到这一点。这就像是作者对你说“仔细观察问题条件,我们容易发现这样一种奇妙的性质..”,怎么个“仔细”法?凭什么我自己“观察”半天就是发现不了呢?霍夫曼本人难道也是死死盯着问题“观察”了一学期然后就“发现”了么?我们有理由相信霍夫曼肯定尝试了各种各样的方法,作出了各种各样的努力,否则当年Shannon都没搞定的这个问题花了他一学期,难道他在这个学期里面大脑就一片空白(或者所有的尝试全都是完全不相干的徒劳),然后到学期末尾忽然“灵光一现”吗?
如果“仔细观察”:),我们会发现两个cost function表达中frequency的概念有微妙的差异,在第一个cost function中,只有叶子节点有frequency,而这个frequency必须和叶子节点的深度相乘。而在第二个cost function中,内部节点也具有了frequency,可是所有节点的“frequency”忽然全都不跟深度相乘了。frequency的不同含义令人困惑。
作者提到:第一个cost function告诉我们频率最低的两个节点必然处于最优编码树的底端,作为最低内部节点的两个子节点。这是一个不严谨的说法,从前文给出的条件和性质,只能推导出编码树的最底层必然能找到频率最低的两个节点,但它们未必一定要是兄弟节点,如果树的最底层不止能容纳两个节点的话它们就可以有不同的父节点。“我们不妨考虑”这样一个例子:对A,B,C,D四个字母进行编码,假设它们的频率分别是1, 1, 2, 2。这个时候我们可以构造如下图所示的两棵树,两棵树的cost都是12,都是最优的。但其中一棵树中,两个频率最低的节点并非兄弟。
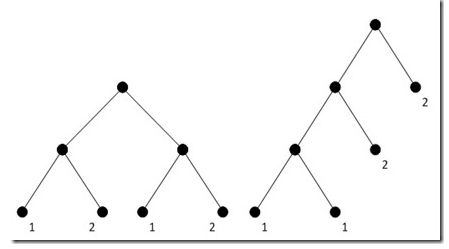
为什么要提到上面这几点不显然和不严谨的地方,因为只要当你看到算法书上出现不显然和不严谨的地方,基本上就意味着作者其实跳过了关键的思维步骤。
不幸的是《Algorithms》这本书里面讲霍夫曼编码已经算是讲的好的了,如果你翻开著名的CLRS,看一看当中是怎么证明的,你就知道我说的什么意思了。有时候这些证明是如此的企图追求formal和严谨,一上来就定义符号一大摞,让人看了就想吐。
说了这么多,有没有可能把霍夫曼编码讲的更好呢?前面说过,霍夫曼编码我记了又忘,忘了又记,好几次了,有一次终于烦了,心想如果要自己去证明,会怎么去证,那个时候我已经忘了《Algorithms》里面怎么讲的了。所以我得从头来起,首先,对于算法问题,有一个一般性原则是,先看一看解空间的构成。尤其是对于搜索问题(最优化问题可以看做搜索问题的一个特例),这一点尤其重要。霍夫曼编码的可能的编码树是有穷的,如果穷举所有的编码树,然后找到那棵代价最小的,这种方法至少是可行的,有了可行的方法(即便是穷举)至少让我们内心感到踏实。
接下来便是提高搜寻效率的问题。而提高搜寻效率的关键(同样也是一个一般性原则),便是尽量去寻找问题条件能够推导出来的性质,****然后利用这些性质去避免不必要的搜寻,只要你学过二分搜索就应该理解这个一般性原则:二分搜索的效率之所以高于“穷搜”(O(n)),便是因为它利用了问题中的性质(有序)来避免了不必要的搜寻。有时候这个性质甚至可以直接将时间降为O(1),例如在一个有序数组中寻找出现次数大于n/2的数(假设该数存在),利用“该数一定出现在数组正中间”这个性质,我们直接就避免了所有的计算。
不过,话虽如此,有时候这些性质并不是那么“显然”的,需要对问题进行深入的折腾才能有可能发现。第三个一般原则:如果你要搜寻的元素是某个满足特定条件的元素(例如寻找最优解的时候,“最优”的定义就是这个“特定条件”),那么可以“倒过来推”(数学证明常用手法,结论当条件使),即假设你已经找到了你要找的元素,那么能得出哪些结论,每一个结论都是最优解的一个必要条件,而每一个必要条件都能够帮助你避免不必要的搜寻,因为你只要发现某个候选解不满足某个必要条件,就可以立即将其丢弃,前面提到的寻找出现次数大于n/2的例子是一个极端情况,我们得出的必要条件导致我们可以直接丢弃除中点元素之外的一切其他元素,再例如如果有人叫你寻找有序数组中最小元素,你会毫不犹豫地把该数组头尾元素中较小的那个给他,因为你知道“如果那个最小元素存在,那么它必然位于头尾”——这个必要条件直接允许你丢弃掉n-2个候选解。
回到霍夫曼编码问题,按照这个原则,我们会去假设已经得到了最优编码树,那么我们能够发现关于它的什么性质呢?这里又要提到另一个适用于很多最优化问题的原则(前面提到的原则适用于一般性搜索问题),所谓最优解,就是说比其他所有解都要更好,虽然这句话听上去像是废话,但是它的一个直接推论——比与它邻近的所有候选解都要好——就是一个非常有用的,不是废话的性质了。学过微积分的都知道,光滑函数的最值点必然是大(小)于其邻域内的所有点的,然后再根据这个就自然推出该点的一阶导数(切线斜率)必然为0的性质,这个性质(必要条件)让我们直接省掉了去整个区间内搜索的麻烦,从而可以直接锁定有限几个候选解。那么,既然我们说最优霍夫曼树一定比它“附近”的树更好,我们就想看看,怎么来找到它附近的树。我们知道要从一个点到它附近,往往是对这个点进行一些调整,例如N+1是到达附近的另一个整数。霍夫曼树是一棵树,所以对这棵树的所有的一次“改动”(或“折腾”)都能够到达与它的“改动”距离为1的点(是不是想起“编辑距离”这个概念),怎么改动呢?最符合直觉的(虽然并不是唯一的)改动便是把叶子节点进行互换。
于是我们得到一个重要的推论:
在最优霍夫曼树中,无论互换哪两个叶子节点,得到的树都变得更“差”。(严格来说是不会变得更“好”,因为最优树未必唯一)
这个性质看上去有点像废话,值得费这么多事么?值得。因为虽然前文说了很多,但都是大多数人大脑里面既有的,一般性的法则,前面说过,如果我们能够从我们已经掌握的一般法则出发来推导出问题的解,那么记忆负担是最小的,因为这里面用到的所有法则我们都很清楚,也知道怎么一步步往下走。
上面这个性质究竟意味着什么呢?如果你假设这两个叶子节点的频率为f1和f2,深度为d1和d2,互换它们的时候,其他叶子节点的cost保持不变,令为常量C,那么互换前总cost为C+f1d1+f2d2,互换后为C+f1d2+f2d1,既然互换之后的树一定更”差“那么就是说f1d1+f2d2 < f1d2 + f2d1,简单变换一下就得到结论:f1(d1-d2)
有了这个结论之后,我们便能够对最优霍夫曼树的构建走出确定性的一步,即,将频率最低的两个叶子节点放在最底层。别小看这一步,这一步已经排除了大量的可能性。这里,我们容易一开始天真地觉得最底层只有这两个叶子节点,于是它们拥有共同父节点,这样一来霍夫曼树的整个拼图便已经拼好了一个小小的角落。
然后我们会发现,要是它们不是兄弟怎么办呢?这里提到另一个一般原则——归约。不是兄弟的情况能否归约为是兄弟的情况?反正我们要求的是一个最优解,而不是所有的最优解,我们只需证明,如果当这两个最低频率的叶子不是兄弟的时候的确存在着某棵最优霍夫曼树,那么通过交换它们各自的兄弟,从而让这两个叶子团聚之后,修改后的树仍然是最优的就可以了。事实情况也的确如此,证明非常直接——既然这里涉及到的所有4个节点都在最底层同一个高度上,那么互相交换的时候不会改变他们任何一个人的深度值,所以总cost不会改变。
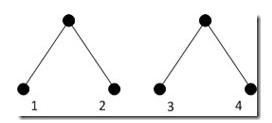
但是接下来我们犯了难,整个树的一个小小的樱桃状的局部是确定下来了,接下来怎么办呢?一个最自然的思路就是考虑第三小的叶子,因为前面说了,元素频率越低就越位于树的底部嘛。第三小的叶子有两种可能的归属,一是跟最小的两个叶子同样位于最底层(这不会违反我们前面得到的推论),这个时候第三小的叶子的兄弟叶子肯定是第四小的叶子,如下图:
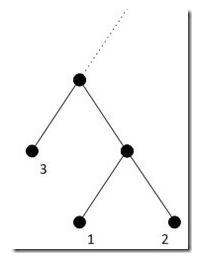
另一种归属就是往上一层去(注意,一旦第三小的叶子往上去了一层,那么剩下的所有叶子都必须至少在这个层以上),往上一层去了之后,它的兄弟是谁呢?不妨将它和刚才第一第二叶子的父节点结为兄弟(前面证明过,同层之前节点互换不会改变编码的cost),如下图:
可是现在问题出现了:虽然第一步构建(最小的两个叶子)是确定的,但是到了第二步摆在我们面前的就有两个选择了,到底选择哪个呢?一个办法就是把两种选择都记下来,然后继续往下走。可是别小看两种选择,接下去每一步都有两种选择的话就变成指数复杂度了。所以现在我们便有了动机回头看一看,看问题中是否有什么没有发现的性质能够帮助我们再排除掉其中一个选择。理想情况下如果每一步都是必然的,确定的,那么N步我们就可以构建出整棵树,这是我们希望看到的,抱着这个良好的愿望,我们仔细观察上面两种构型,一个自然而然的问题是:这两种构型都有潜质成为最优解吗?如果我们能够证明其中一种构型不能成为最优解那该多好?就省事多了嘛。这里引入另一个一般性的解题法则:特例。我们的大脑喜欢具体的东西,在特例中折腾和观察会方便的多。
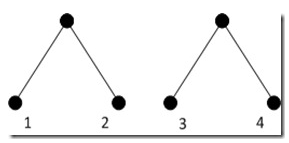
上面这个{1, 2, 3, 4}的例子就是个很好的特例,如图(注:图中节点旁的数字一概为频率值,而非编号):
多加折腾一番也许我们不难发现,如果将1,2及其父节点跟叶子4进行交换(注意:交换的时候1,2也被一同带走了,因为反正1,2两个节点已确定是好兄弟永远不会分家了,折腾的时候只能作为一个整体移动,所以这里也可以说是交换子树),那么树的编码将会变得更优,因为这样一次交换会将1和2的深度+1,意味着整棵树的代价+3,而同时会将叶子4的深度-1,也就是说整棵树的代价-4,总体上整棵树的代价就是+3-4=-1(注意,在计算的时候我们只需考虑被交换的局部,因为树的其他部分的代价保持不变)。如下图:
这个交换启发了我们,其实前面一开始说的交换两个叶子节点可以推广为交换内部节点和叶子节点,然后很快我们就会意识到其实可以推广到交换任意两个节点。(注意,当我们说交换内部节点的时候,其实是连同该内部节点作为局部根节点的整个子树都交换过去)于是前面我们的推论就可以推广为:
在最优霍夫曼树中,无论互换哪两个节点,得到的树都变得更“差”(交换内部节点则是连同该内部节点作为局部根的子树一同带走)
这个推论很容易理解,只不过是多增加了一种“编辑”最优霍夫曼树的方法罢了(记住最优霍夫曼树无论怎么“编辑”都不会变得更“好”,包括“交换子树”这种“编辑”),我们前面没有想到这种“编辑”方法是因为它不那么显然,而且当时我们已经想到一种最直接的“编辑”方法了,即交换叶子,就容易顺着那个思路一直走下去,直到我们发现必须寻找新的性质,才回过头来看看有没有其他法子。
当然,并不排除一开始就想到这种推广的可能性,问题求解的过程并不是这么线性的,如果我们习惯了推而广之的思维,也许一下就能想到这个推广来。类似的,也不排除从另一种思路出发想到这种推广的可能性。所以这里只是可能的思维轨迹中的一种,重点在于其中并没有某处忽然出现一个不知从哪里冒出来的,神启一般的结论。
刚才提到,构造最优树的第二步是考虑第三小的叶子,但也有另一种常见的思维:考虑到第一步(即选取频率最小的两个叶子)所做的事情是从N个叶子中选择两个黏在一起作为兄弟,那么也许对于一些人来说自然而然的第二步就是试图继续选取两个节点黏在一起作为兄弟(注意这里不仅可以选择叶子,也可以选择已经生成的内部节点),然后依次类推来拼完整棵树。按照这一思路,第二步的选项仍然还是集中在第三小的叶子上,因为这个选择要么是让第三第四小的叶子结拜为兄弟,要么是让最小两个叶子的父节点和第三小的叶子结拜。
回到刚才我们的推论:在最优霍夫曼树中,无论互换哪两个节点,得到的树都变得更“差”(交换内部节点则是连同该内部节点作为局部根的子树一同带走) 。根据这个推论我们容易计算出,在最优霍夫曼树当中,两个内部节点n1和n2,如果n1比n2更深,那么n1下面的所有叶子的频率之和必然要小于n2下面所有叶子的频率之和。如果交换的是一个内部节点和一个叶子节点,则道理是类似的。这个性质的证明和上面的类似,就不赘述了。
这个性质暗示了一个重要的推广结论:如果我们把每个内部节点的所有叶子的频率之和标在它旁边,那么整棵树的每个节点便都有了一个数值,这个数值遵循统一的规律:即越往深层越小。这就意味着,我们刚才的二选一困境有办法了!当我们将最小的两个叶子f1和f2合并的时候,生成了一个新的节点M,这个节点有一个数字(为两个叶子的频率之和f1+f2),根据上面的推论,这个数字f1+f2跟所有频率一同,遵循最小的在最底层的原则,所以我们下一步必须在剩下的那些互相之间关系待确定的节点(叶子节点和内部节点)之中,即{(f1 + f2), f3, f4}里面选择最小的两个数字结合成兄弟(由于f1和f2这两个节点已经铁板钉钉结为整体了,所以从集合里面可以看做移除)。到这里,我们就发现递归已经出现了,接下去的过程对于绝大多数人应该就真的很显然了。
以上的解释,比《Algorithms》更简短吗?显然不是。反而要长得多(其实真正的思维过程比这要更长,因为中间还会涉及各种不成功的尝试)。但是它比《Algorithms》当中的版本更不容易被忘记,因为其中关键的思维拐点并不是毫无来由的,而是从你已经熟知的,或者说虽然不知道,但容易理解的一般性解题法则出发自然推导出来的,所以你基本上不需要记忆什么东西,因为你需要记的已经在你脑海中了。
在上面的证明过程中,还有一个不像看上去那么显然的事情:在我们寻找最优霍夫曼树的时候,我们曾经试图去比较假想的最优树和它的“临近”的树,从而去探索最优树的性质。但是,究竟什么是临近的树?在前面的讲解中,我们说如果交换A和B这两个叶子节点,便得到一颗不同的树,可以看做和原树的“编辑距离”为1的树。但是,真的这么显然么?难道除了交换叶子的位置,就没有其他办法去“折腾”这棵树了?后来我们看到,可以交换子树而不仅仅是叶子,而交换子树让我们得到了至关重要的推论。此外,如果不是交换,而是像AVL树那样“旋转”呢?说到底,二叉树是一个离散的东西,并不像连续值那样,天生就有“距离”这个概念,如果我们离散而孤立地去看待所有的树,那么没有什么临近不临近的,临近本是一个距离的概念,除非我们定义树和树之间的距离函数,才能说临近与否,而距离函数怎么定义才是“显然”的呢?
还有,其实以上只是试图给出最优霍夫曼树的证明的一个更自然的过程,而当年霍夫曼面临这个问题的时候根本还没有人想到要用二叉树呢!更不要说在二叉树的前提之下进行证明了。根据wikipedia的介绍,霍夫曼同学(当年还在读Ph.D,所以的确是“同学”,而这个问题是坑爹的导师Robert M. Fano给他们作为大作业的,Fano自己和Shannon合作给出了一个suboptimal的编码方案,为得不到optimal的方案而寝食难安,情急之下便死马当活马医扔给他的学生们了)当年为这个问题憔悴了一个学期,最后就快到deadline的时候“忽然”想到二叉树这个等价模型,然后在这个模型下三下五除二就搞定了一篇流芳千古的论文,超越了其导师。
最后说两个有趣的现象:也许很多人会觉得,越是大师来写入门教科书越是好,其实很多时候并非如此,尤其是在算法设计和数学领域,往往越是在其中浸淫久了越是难写出贴近初学者的书,因为大量对初学者来说一点都不显然的事情在他看来已经是“不假思索”了,成了他的内隐记忆,尤其是当他想要和你解释一个复杂的东西的时候你就会发现他会常常逻辑跳跃,满嘴跑术语,根本没有意识到别人对有些术语和隐含的逻辑根本没有像他那样的理解。
最适合将一个东西讲给别人听的时候并不是等懂了很多年以后,而是刚刚弄懂的时候,这个时候从不懂到懂的差别记忆还非常鲜明,能够清清楚楚地记得到底是哪些关键的地方是最折磨人的,也最能够站在不懂者的角度来思考问题。像波利亚这样,成了大师还能够站在不懂者角度去换位思考的,可以说是凤毛麟角。所以说前Amazon CAO(首席算法官)的《Introduction to Algorithms: a Creative Approach》绝对是本罕见的好算法书)
知其所以然(一)里面曾经提到,要弄清来龙去脉,最好去看看原始作者是怎么想的,可是正如上文所说,即便是最初的发明者,在讲述的时候也会有意无意地“线性化”,我就去查看了霍夫曼最初的论文,那叫一个费解,不信你可以自己看看(PDF)。
可以归约为搜索算法的问题(非常多)一般来说相对还是有一些头绪的,因为搜索空间一般还比较容易界定,难点在于要从问题的条件中推导出用于节省搜索的性质。而策略设计问题则完全是另一个世界,因为策略的设计空间貌似是可列无穷的,常常让人感觉无从下手,摸不着头绪,许多让人挠头的智力问题就有这个特点(例如著名的100个囚徒和1个灯泡的房间就让很多人有这种感觉),策略设计问题也有一些较通用的法则,以后再说。
怎么才能在学算法的时候学到背后的东西呢?有以下几点很重要:
不要觉得每个步骤都很显然,每个nontrivial的算法背后都有一段艰辛的探索经历,觉得显然的话必然是一种幻觉。Stay foolish,才能发现某些环节其实并不是那么显然的。
检验是否真正理解的最佳方法就是过一段时间之后,自己试着证明一次。如果真正理解了的话,你的证明便会比较顺畅。如果当时没有真正理解,那么凡是那些你当时觉得显然但其实不显然的地方,都会成为你证明里面缺失的环节。
对于一个算法,多寻找各种来源的资料,也许能够找到一个讲的比较深刻的。我在《数学之美番外篇:快排为什么那么快》和《知其所以然(一)》里面都举到了这样的例子。
多试着去抽象背后的一般性法则,即便后来发现抽象得是错的,也比不去抽象要好。抽象是推广的基础。只有抽象出更深层的法则,才能让你事半功倍,触类旁通,否则一个萝卜永远是一个坑。(注意,其实我们的下意识是会进行一定程度的抽象的,例如前面提到的原始人的例子,小溪和小河(或者小沟)细节上是不同的,但本质上是一样的,我们的大脑会自动进行这种简单抽象,提出事物的共性。正因此,即便你不去有意识地总结一般规律,只要你看的足够多,练的足够多,必然就会越来越谙熟。)
最后留个问题:虽然按照上文的方式来构造霍夫曼树一定能够得到一个最优树,但是怎么证明一定能得到呢?乍一看这个问题似乎很多余,因为证明很简单:我们拼装整棵树的每一步都没得选,而且每一步都必然拼凑出最优树的一个小小局部,如果最终还没有得到最优树的话,只能说最优树是不存在的了,然而最优树是一定存在的,因为所有树的集合是有穷的,有穷集必有最值,因此证毕。这个证明固然是没问题的,但它其实是一个间接证明,换句话说,我们在构建树的过程中的逻辑是这样的:“之所以我们选择粘结n1和n2,是因为其他粘法必然违反最优树的两个性质。所以我们别无选择。”但是,这并没有说,我们选择了粘结n1和n2,一定就符合了最优树的性质。(也就是说“其他做法都是错”并不能推出“这种做法必然对”,这就像是你在一大堆豆子当中寻找一个特殊的豆子,你拿起一个,看看不是,扔掉,又拿起一个,还不是,扔掉,排除到最后只剩一个豆子了,假设你又知道这个特殊的豆子必然存在,那么这个时候你根本不用看就知道这个豆子一定就是你要找的)那么,你能否直接证明,拼装最优树的过程每一步都符合最优树的性质呢?
编辑:黄飞
-
算法
+关注
关注
23文章
4615浏览量
92962
原文标题:为什么算法这么难???
文章出处:【微信号:AndroidPush,微信公众号:Android编程精选】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
为什么总说VR定位动捕威廉希尔官方网站 难 它究竟难在哪里?
请问不同编程语言的区别到底在哪里?
iPhone8到底好在哪里?为何敢买那么贵?又为何还有那么多人买?
小米MIUI8.2你到底好在哪里?到底值不值得升级呢?
“缺芯”之痛,到底痛在哪里?
同品牌下,电视价格的差距到底在哪里?
LoRa到底“神”在哪里?





 算法到底难在哪里?
算法到底难在哪里?











评论