一、摘要
相位响应是信号处理领域中一个重要的概念,描述了信号在系统中传输过程中的相位变化。相位响应在时域和频域分析中起着关键作用,对信号的特性和系统性能具有重要影响。本文将详细介绍相位响应的概念、计算方法,并给出Python示例代码,帮助读者更好地理解和应用相位响应。相位响应是信号处理中不可忽视的概念,它描述了信号在系统中传输过程中相位的变化。相位响应是频率响应的重要组成部分,对信号的时域和频域特性具有关键影响。了解相位响应的概念和计算方法对于信号处理的理解和应用至关重要。
二、相位响应的定义
相位响应是指系统对不同频率的输入信号在传输过程中引起的相位变化。它是一个频率的函数,用于描述信号的相对延迟或提前。相位响应是信号在系统中经过时延、滤波和频率选择等操作后的结果。
三、相位响应的计算方法
相位响应的计算方法取决于系统的类型和表示方式。对于线性时不变系统,可以使用频域方法或时域方法来计算相位响应。频域方法利用系统的频率响应和幅度响应来推导相位响应,而时域方法则通过系统的冲激响应进行计算。
四、Python示例
计算相位响应 下面是一个简单的Python示例代码,演示如何使用NumPy和SciPy库来计算信号的相位响应。
from scipy import signal
import matplotlib.pyplot as plt
import numpy as np
b, a = signal.iirfilter(9, Wn = 400,btype='lowpass', analog=True, ftype='butter', output='ba')
w, h = signal.freqs(b, a,worN=np.linspace(0,1000,10000))
fig, ax1 = plt.subplots()
ax1.set_title('Magnitude response(dB) and Phase Response')
ax1.plot(w, 20 * np.log10(abs(h)), 'b')
ax1.set_ylabel('Amplitude(dB)', color='b')
ax1.set_xlabel('Frequency(Hz)')
ax2 = ax1.twinx()
angles = np.unwrap(np.angle(h))
ax2.plot(w, angles, 'g')
ax2.set_ylabel('Phase(radians)', color='g')
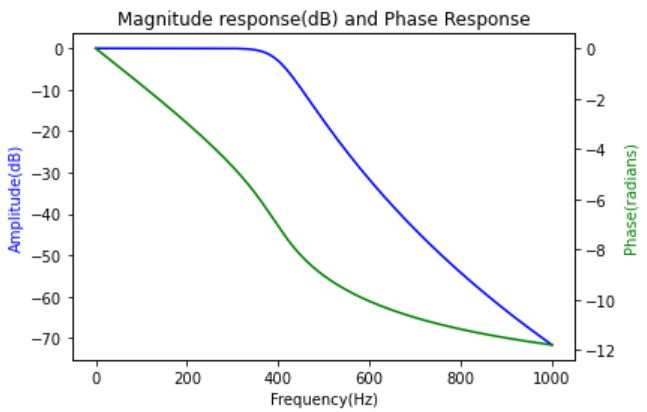
unwrap 函数在频率分析中也很有用。unwrap 根据需要对相位增减若干个 360° 以将其展开,使之在 360° 相位不连续点处保持连续。要了解 unwrap 的作用,请设计一个 25 阶低通 FIR 滤波器:
h = signal.firwin(25, 0.4)
用 freqz 获得频率响应,并以度为单位绘制相位:
f,H = signal.freqz(h,1,512,2)
angles = np.angle(H)
fig, ax3 = plt.subplots()
ax3.plot(f, angles*180/np.pi, 'g')
ax3.set_ylabel('Phase(radians)', color='g')
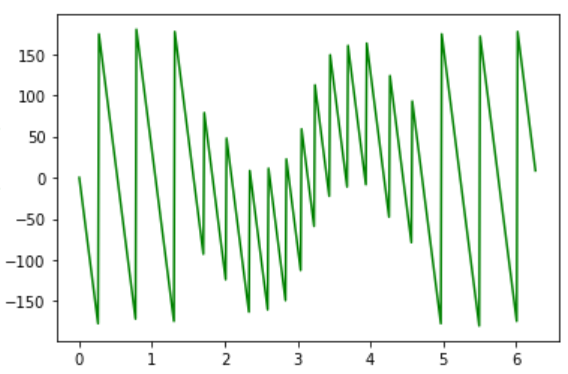
很难将 360° 跳跃(由 angle 中反正切函数的定义导致)与 180° 跳跃(表示频率响应为零)区分开来。unwrap 消除了 360° 跳跃
fig, ax4 = plt.subplots()
ax4.plot(f, np.unwrap(angles)*180/np.pi, 'g')
ax4.set_ylabel('Phase(radians)', color='g')
ax4.set_xlim([0, 3])
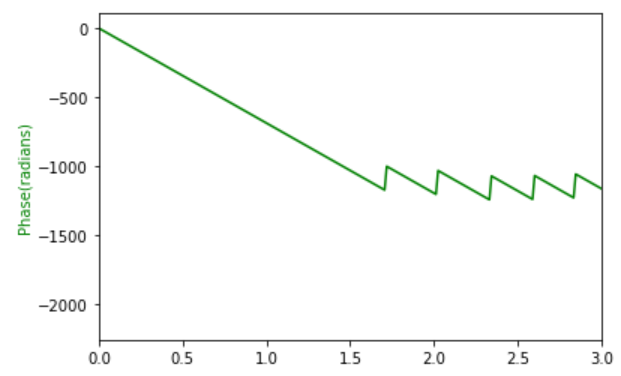
在示例中,我们以低通滤波器为例进行相位响应的计算和展示,但实际上,相位响应的计算方法和应用并不仅限于滤波器。它在音频处理、图像处理、通信系统等领域都有广泛应用。
五、结论
相位响应是信号处理中重要的概念,描述了信号在系统中传输过程中的相位变化。了解相位响应对于理解信号的时域和频域特性、优化系统设计以及实现信号处理算法等具有重要意义。通过Python示例代码,我们可以计算和可视化信号的相位响应,帮助读者更好地理解和应用该概念。
-
低通滤波器
+关注
关注
14文章
474浏览量
47409 -
信号处理器
+关注
关注
1文章
254浏览量
25275 -
fir滤波器
+关注
关注
1文章
95浏览量
19041 -
python
+关注
关注
56文章
4796浏览量
84668 -
相位响应
+关注
关注
0文章
3浏览量
5731
发布评论请先 登录
相关推荐




 相位响应信号在系统中传输过程中的相位变化
相位响应信号在系统中传输过程中的相位变化













评论