支持向量机（兵（车）王问题程序设计）

兵（车）王问题的样本数据集包含六个维度，六个维度代表三个棋子在棋盘中的位置。总样本数为28056个，其中，正样本（和棋）数量为2796个，负样本（白方胜）数量为25260个。

一、数据预处理

28056个样本中的随机5000个样本被用于样本训练（即此5000个样本为训练样本），其余样本被用于测试（即其余样本为测试样本）。

然后，求出训练样本每个维度的均值和方差，并将训练样本和测试样本归一化，各个维度归一化后的值与原值的等量关系为：

newX=(X-meanX)/std(X) 样本归一化可将数据集的每个维度的值限定于一个固定范围内，从而减少因各个维度取值范围的差异而导致的训练误差。

二、设置支持向量机的参数

（1）-s “-s”表示支持向量机不同的形式。因为兵（车）王问题属于二分类问题，且最优化问题的目标函数为1/2||ω||2+C∑δi（式①），所以-s的取值为0。-s的数值处于1~4所分别对应支持向量机的形式可查询LIBSVM工具包或其他资料。



图片来源：中国慕课大学《机器学习概论》

（2）-t “-t”参数确定支持向量机的核函数K(X1,X2)。LIBSVM工具包支持的核函数包括：LInear（线性内核，-t=0）、Ploy（多项式核，-t=1）、Rbf（高斯径向基函数核，-t=2）、Tanh（sigmoid核，-t=3）、自定义核（，-t=4）。



图片来源：中国慕课大学《机器学习概论》

1）线性内核 线性内核的表达式为K(x,y)=xTy。线性内核具有理论意义，但因为使用线性内核求解支持向量机与不使用核函数求解支持向量机无差别（个人理解：因为线性内核的核函数都可以求出其对应的φ(x)，所以不使用核函数也可以求解），所以线性内核不具有实际使用价值。

2）多项式核 多项式核的表达式为K(x,y)=(xTy+1)d。多项式核是维度可以调节的函数，表达式中的d越大，对应的φ(x)维度越高。

3）高斯径向基函数核 高斯径向基函数核的表达式为K(x,y)=e-(||x-y||2)/σ2。表达式中的σ是人为设置的超参数，该函数的维度是无限的。课程中建议：若处理实际问题中不知道选择哪种核函数，则首选该函数。

4）sigmoid核 sigmoid核的表达式为K(x,y)=tanh(βxTy+b)，其中，tanh(x)=(ex-e-x)/(ex+e-x)。表达式中β、b均是人为设置的超参数，该函数的维度是无限的。

5）自定义核 因为支持向量机通过求解其优化问题的对偶问题： 最大化：θ(α,β)=∑αi-1/2∑∑yiyjαiαjφ(Xi)Tφ(Xj)；

限制条件：

（1）0≤αi≤C，i=1~N；

（2）∑αiyi=0，i=1~N。（式②） 的αi求解可用于样本分类的超平面，所以若开发人员已知图一核函数矩阵的具体形式，则其可通过输入该核函数矩阵求解用于样本分类的超平面（个人理解：将核函数矩阵中各个核函数值替换φ(Xi)Tφ(Xj)即可求解超平面）。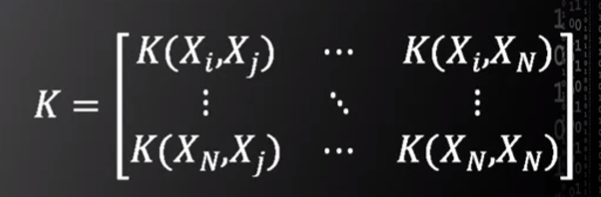



图片来源：中国慕课大学《机器学习概论》

（3）-c “-c”代表式①和式②中C的值（式①和式②中C为同一参数）。

（4）-g（gamma） “-g”所代表的值与所选择的核函数有关，例如：若选择Rbf为核函数，则-g代表1/σ2。

审核编辑：刘清