本文很好地介绍了interwetten与威廉的赔率体系 滤波器。它涵盖了基本的一阶和二阶滤波器类型以及无源和有源滤波器的优缺点。本文使用多个运算放大器实现示例推导并分析了基本的双二阶实现方案。
滤波器设计的世界通常被认为是黑魔法,因为有无数的配置、独特的术语和复杂的方程式。本应用笔记将介绍不同的滤波器类型,阐明术语,并为选择提供基础,使滤波器的设计更加科学,少了一点魔力。我们将主要关注低通滤波器,尽管带通和高通滤波器都可以使用相同的方法进行分析和设计。
出现的第一个问题是:我是否可以使用简单的无源滤波器(即仅使用电阻器、电容器和电感器等无源元件,而不使用运算放大器),还是最好使用有源滤波器。无源滤波器的优点是设计和实现非常简单。它还提供一个简单的单极或两极滤波器,其电响应可以轻松计算。对于单极点低通滤波器,fc = 1/(2 × π × RC),滤波器滚降为每倍频程6dB或20dB/十倍频程。但是,此过滤器确实有一些明显的缺点:
它对元件值公差非常敏感。
对于低频,R和C的值可能相当大,导致物理上较大的组件。
一阶或二阶滤波器可能无法提供足够的滚降
如果电路中需要增益,则不能将其添加到滤波器本身。
滤波器可能具有高输出阻抗。由于电阻值通常很大,为了保持电容的合理值,下一级器件可以看到显著的源阻抗。可以在输出端增加一个运算放大器,但是,除了降低输出阻抗之外,它还可用于改善滤波器的性能,为什么要在这里添加运算放大器呢?
如果无源滤波器不能满足您的需求,您可以选择有源滤波器。通过增加运算放大器,我们可以轻松实现二阶滤波器。二阶滤波器通常是高阶滤波器的构建块,因为它们可以很容易地级联以获得高阶滤波器。滤波器的一般形式可以写成等式形式,如下所示:
H(s) = K (s + z1)(S + z2)/[(s + p1)(s + p2)]
这个方程称为双二次方程,简称为双二元方程。分子中的zn项表示零,分母中的pn项表示极点。查看等式,首先清楚的是可以以这种形式编写的过滤器是双二阶。这意味着Sallen-Key滤波器,状态变量变量滤波器,多反馈滤波器和其他类型的都是双二阶的。还有一个“双四”拓扑来帮助进一步混淆事物。因此,真正的滤波器名称是双二阶 Sallen-Key、双二阶状态变量和二阶(稍后会解释)。
以低通滤波器为例,低通滤波器可以用一般方程形式编写为:
H(s) = K/(as² + bs + 1),其中 a = R1R2C1C2 和 b = R1C1 + R2C1
这可以通过使 R1 = R2 和 C1 = C2 来简化,从而得到:
H(s) = K/(R²C²s² + 2RCs + 1)
低通二阶Sallen-Key滤波器的框图如图2所示。该滤波器也称为正反馈滤波器,因为输出反馈到运算放大器的正端。这种拓扑很受欢迎,因为它只需要一个运算放大器,因此相对便宜。
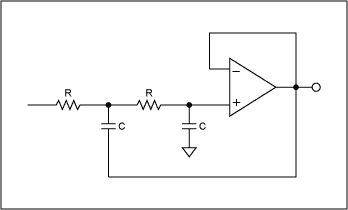
图1.等分量值,萨伦基低通滤波器。
但是,此拓扑存在一些缺点。首先,它可以获得的最大Q值非常有限,因此不建议用于需要高Q值的应用。滤波器的Q值是“质量”因子,它基本上给出了存储的能量与共振时耗散的能量之比。高 Q 值滤波器可实现非常尖锐的滤波器滚降。就s平面而言,高Q值滤波器的极点更靠近jw轴。请记住,只要极点位于jw轴的左侧,设备理论上是稳定的。随着极点越来越接近jw轴,稳定性降低。现在回到Q因子。在选择或设计带通滤波器时,通常使用Q因数。Q的倒数是阻尼因数,在低通和高通应用中更为相关。对于单个运算放大器Sallen-Key滤波器,Q值通常约为5左右。
另一个缺点是,与放大器所需的最小开环增益(3Q²)相比,该电路的增益相对较低(-90Q)。这意味着放大器的GBW积必须明显高于滤波器的最大截止频率,从而使放大器的性能高于预期,以确保其不会限制对滤波器响应产生不利影响。
为了获得稍高的Q值,让我们转到图2所示的多反馈无限增益架构。这种拓扑同样需要一个放大器,并提供25范围内的Q值。使用这种拓扑,增益(-2Q²)与放大器GBW积(谐振时为20Q²)相比仍然相对较低,但不如Sallen-Key方法低。
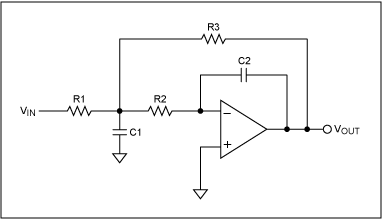
图2.无限脉冲、多反馈低通滤波器。
但请注意,这种拓扑结构反转了信号,并注意到增益和Q值与Sallen键密不可分。Sallen Key和多重反馈架构对外部组件变化也相当敏感。为了转向更可靠的滤波器,我们现在考虑3和4运算放大器状态可变和双二阶架构。
状态变量双二阶
图3显示了3个放大器状态变量Biquad的基本架构。它包括一个求和节点,后跟两个积分器。这种架构非常通用,因为它提供了高通、带通和低通输出,但它也允许独立控制fc和Q。
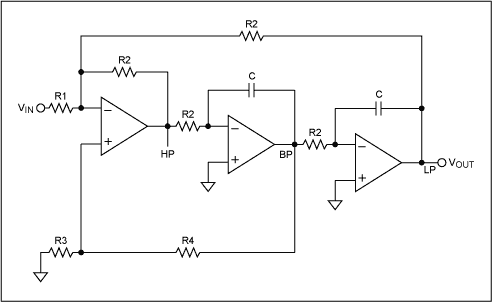
图3.三个放大器状态可变双二阶。
通过增加第 4 个放大器,实现了 Q 和增益的独立控制(图 4)。状态变量是高Q值电路的理想选择。通过适当的滤波器设计,可以轻松达到 500 或更高的 Q。与单运放架构不同,开环增益(3Q)只需略高于滤波器的输出增益(Q),低通增益为Q,这降低了对运算放大器GBW的要求(请注意,对于Sallen-Key,运算环路增益必须至少为90Q²,Q为500时为22.5MHz。
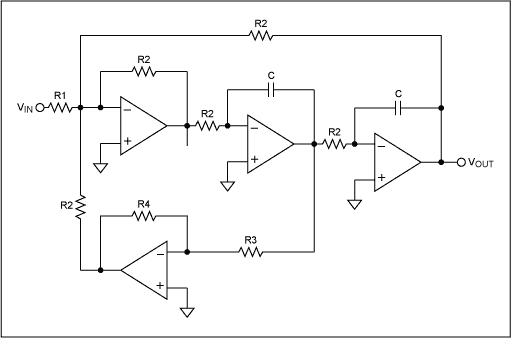
图4.双二阶状态变量滤波器,具有独立控制 q/阻尼。
在到目前为止讨论的拓扑中,起始变量对组件变化最不敏感。它还具有另一个独特的属性:随着频率fc的变化,Q和百分比带宽保持不变。也就是说,当您在频域中移动fc时,Q值保持不变,但滤波器的带宽随着fc的增加而减小,随着fc的减小而增加。带宽百分比定义为 100% × ((F在, gL)/(√ F在×FL) 其中 F在是上 3dB 带宽点,FL是较低的 3dB 带宽点和 √F在×FL是 FC。
状态变量设计的主要缺点是使用3或4个放大器。对于功耗敏感型应用尤其如此。由于可用的过滤器软件和过滤器设计食谱过多,设计本身相当简单。但是,当使用高Q值时,必须非常小心布局和组件选择。这是因为高Q值电路容易表现出不稳定,并伴有轻微的元件不匹配。由于这种不稳定性,它们也更有可能振荡。
双二阶滤波器
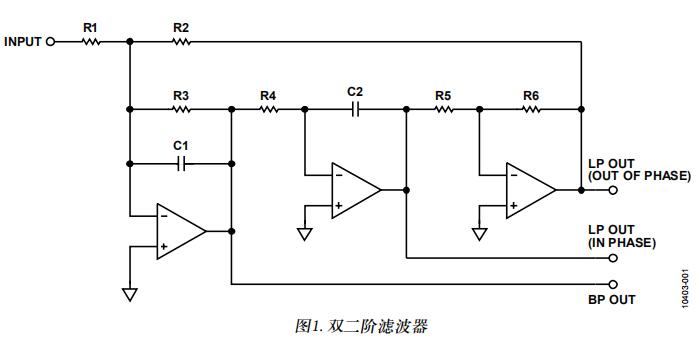
最后,我们看一下双二阶滤波器(图5)。它与上面显示的状态变量双二阶非常相似。然而,它包括一个积分器,然后是一个逆变器,然后是另一个积分器。请注意,这种细微的变化提供了一个行为与状态变量滤波器不同的电路。
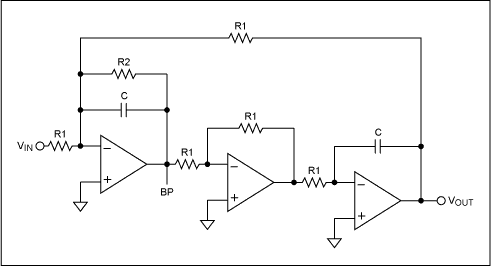
图5.双二阶滤波器。
最大的区别在于,对于双二阶,当fc发生变化时,带宽保持不变,但Q值会发生变化。因此,如果在频域中更改fc,随着fc的增加,Q值增加,随着fc的减小,Q值也会减小。除了这种差异之外,双二阶运算的行为类似于状态变量。它允许非常高的Q值,可以配置为3或4放大器配置,并且对外部元件变化也不太敏感。3和4放大器电路消耗更多功率,通常需要更多设计时间,特别是当多个级级联以获得更陡峭的滤波器滚降响应时。此外,由于单个放大器比四通道放大器便宜,因此成本更高。从性能的角度来看,它要好得多,这是必须做出的权衡。
您可以使用上述操作放大器威廉希尔官方网站 设计滤波器。Maxim拥有多种高速、高精度运算放大器,可用于滤波器设计。如果您不想自己设计,可以选择MAX274/MAX275集成滤波器。这些单芯片解决方案分别配置为由二阶构建模块组成的 8 阶(8 极)和 4 阶(4 极)滤波器。
这些连续时间滤波器采用双二阶架构,提供低通和带通输出。
审核编辑:郭婷
-
放大器
+关注
关注
143文章
13584浏览量
213368 -
滤波器
+关注
关注
161文章
7796浏览量
177999 -
运算放大器
+关注
关注
215文章
4930浏览量
172850
发布评论请先 登录
相关推荐
通用运算放大器(Op-Amp)应用及分析
运算放大器设计与应用
运算放大器的电阻噪声与计算示例
常用运算放大器
二阶系统的运算放大器总输出噪声计算




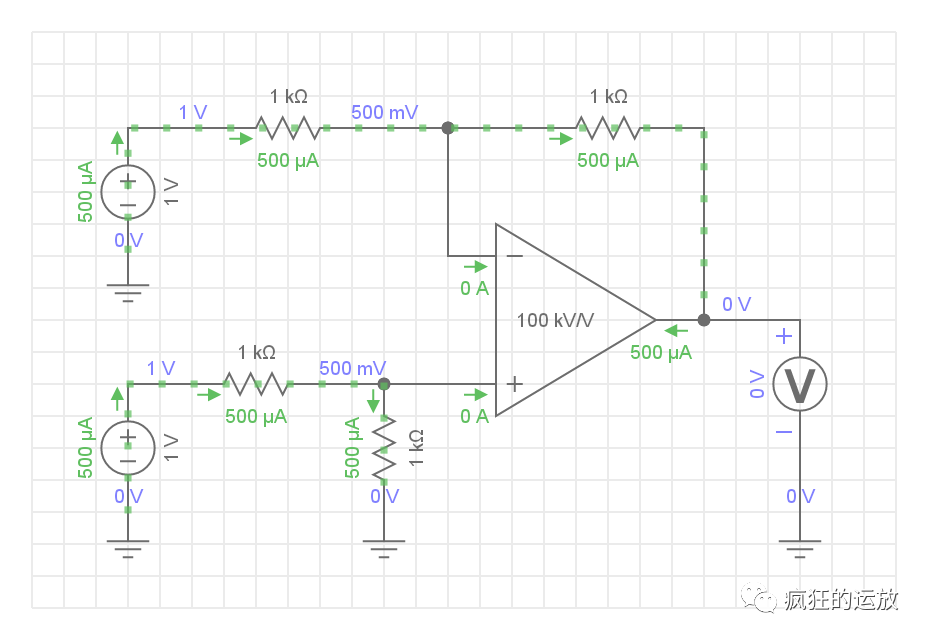
 使用多个运算放大器实现示例推导和基本双二阶实现方案
使用多个运算放大器实现示例推导和基本双二阶实现方案











评论