数字串扰在数据转换器中的影响：串扰对时钟的影响

数据转换器的数据手册经常提到，尽量减少数据转换器时钟的串扰非常重要。当被问及当它存在时会发生什么时，许多工程师都有“它会产生噪音”的见解。虽然这通常是一个真实的陈述，但在更深层次上理解这一点是有价值的，这样设计工程师就可以更有效地理解和排除具有此类问题的电路。

阅读本文后，读者将了解数字数据信号到时钟的串扰如何引起谐波失真和其他信号相关误差问题。如果不了解机制，这些可能需要很长时间来诊断和修复。

在阅读本文之前，了解本系列第一篇文章中的概念将有助于理解。

噪声如何耦合到时钟信号上

在讨论数字位串扰对数据转换器系统的影响之前，了解时钟噪声对数据转换器系统的一般影响非常重要。

数据转换器时钟信号看起来像数字信号。怎么会容易串扰呢？

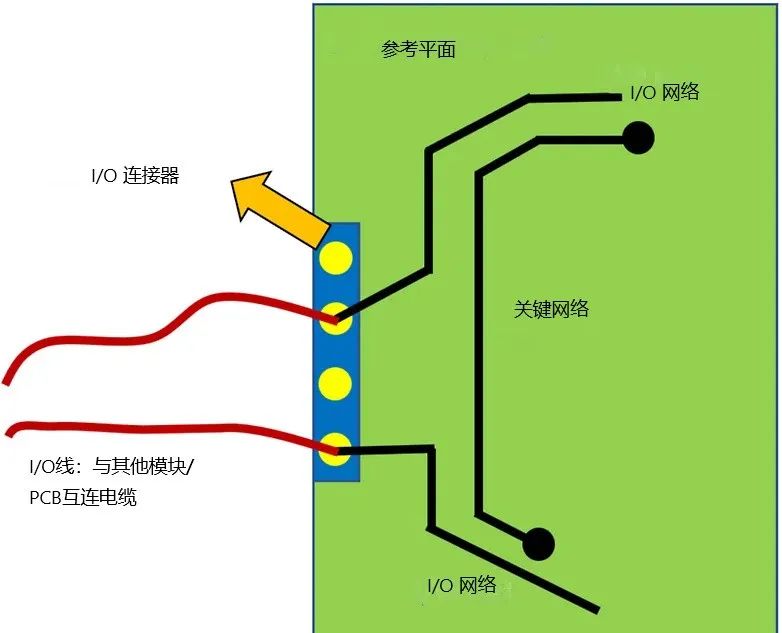
时钟信号标记一个时间点 - 它越过数字信号阈值的点。如果上升/下降/转换时间为零，则无论环境中存在噪声，采样时刻都将被精确定义。但现实世界的时钟在上升和下降中是有偏差的。在此过渡期间，时钟信号是interwetten与威廉的赔率体系 的。如果在阈值交叉附近的压摆期间存在任何电压串扰，则可以改变超过阈值的时间点。这会在时钟上产生噪声，通常称为抖动。

时钟噪声对采样输入信号的影响

数据转换器时钟上的噪声会影响采集数据转换器模拟信号（即ADC输入）样本的时间点。如果模拟信号随时间变化，则将采样与最初预期的电压不同的电压。

时间误差（即抖动）是时钟转换压摆率的函数，与频率无关。这通常是一个惊喜。量化：采样电压中的误差是输入信号电压相对于时间的斜率，乘以时间误差。

dv = （dv/dt） × dt = 斜率 × dt

请注意，该关系与时钟频率无关。唯一重要的是时钟抖动的皮秒和模拟信号的压摆率。

上述等式有许多重要含义，将在下面讨论。

查看这种噪声的另一种方法是将采样信号视为时间的函数。即，

X (t) = sin (f × t).

时间分量由常规抖动时间分量代替。

X jittered (t) = X (t + jitter)

对于一个简单的情况，我们可以假设抖动是正弦波。

抖动 = c × sin （ fj × t ）

这将产生结果：

X jittered (t) = sin (f × [ t + c × sin (fj × t) ] )

请注意，这与相位调制（PM）信号的等式相同。具有相位调制的正弦波是正弦波在其相位/定时位置调制的正弦波。如果ADC使用纯时钟对在Fj调制的正弦波进行采样，则会产生与ADC使用时钟对纯正弦波进行采样相同的样本集，其采样位置以Fj速率抖动。

相位调制或正弦抖动正弦波的净效应是，边带在调制频率及其谐波的距离处出现在正弦波周围。例如，图1显示了频率为4的纯正弦波和频率为4的类似正弦波，频率为2的PM调制/抖动。请注意，噪声分量出现在频率为2及其谐波的边带上。或者，给出精确的数字：“正弦波频率”±N ד调制频率”或 4 - 2 = 2、4 + 2 = 6、4 + 2 × 2 = 8、4 + 3 × 2 = 10 等。

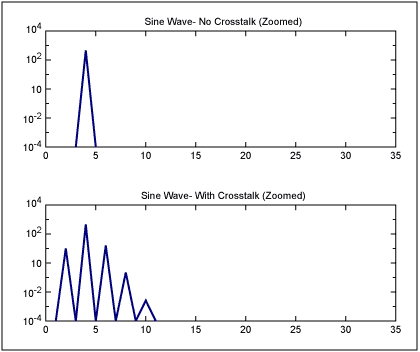
图1.频率为 4 的纯正弦波，以及频率为 2 的 PM 调制的相同正弦波（相当于频率为 2 的时钟串扰）。

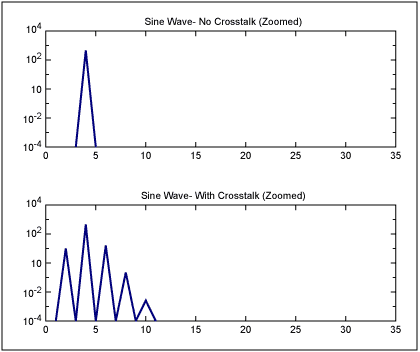
现在，让我们看一下上述一种更特殊的情况：当串扰/相位调制与原始信号处于同一频率时。答案遵循与上述相同的原则和模式。边带出现在串扰频率及其谐波的频率距离处。图2显示了这样一个例子：频率为4的正弦波，频率为4的PM调制/时钟噪声。请注意，边带出现在 4 + 4 = 8、4 + 2 × 4 = 12、4 + 3 × 4 = 16 等频率下。

你能把这和谐波失真区分开来吗？

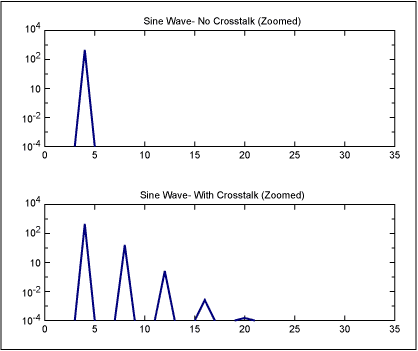
图2.频率为 4 的纯正弦波，以及频率为 4 的 PM 调制的相同正弦波（相当于频率为 4 的时钟串扰）。

结论

我们为什么要分析这个晦涩难懂的案例？因为这与ADC的数字数据信号串扰到时钟时发生的情况直接相关。噪声源是数字数据信号能量。由于电容耦合机制，这种能量在时钟上产生与时钟相同频率的正弦“噪声”。

审核编辑：郭婷