到目前为止,我们已经用小批量随机梯度下降训练了我们的模型。然而,当我们实现该算法时,我们只担心通过模型进行前向传播所涉及的计算。当需要计算梯度时,我们只是调用了深度学习框架提供的反向传播函数。
梯度的自动计算(自动微分)大大简化了深度学习算法的实现。在自动微分之前,即使是对复杂模型的微小改动也需要手动重新计算复杂的导数。令人惊讶的是,学术论文常常不得不分配大量页面来推导更新规则。虽然我们必须继续依赖自动微分,以便我们可以专注于有趣的部分,但如果您想超越对深度学习的肤浅理解,您应该知道这些梯度是如何在底层计算的。
在本节中,我们将深入探讨反向传播(通常称为反向传播)的细节。为了传达对威廉希尔官方网站 及其实现的一些见解,我们依赖于一些基本的数学和计算图。首先,我们将重点放在具有权重衰减的单隐藏层 MLP 上(ℓ2 正则化,将在后续章节中描述)。
5.3.1. 前向传播
前向传播(或forward pass)是指神经网络从输入层到输出层依次计算和存储中间变量(包括输出)。我们现在逐步了解具有一个隐藏层的神经网络的机制。这可能看起来很乏味,但用放克演奏家詹姆斯布朗的永恒名言来说,你必须“付出代价才能成为老板”。
为了简单起见,我们假设输入示例是 x∈Rd并且我们的隐藏层不包含偏差项。这里的中间变量是:
(5.3.1)z=W(1)x,
在哪里W(1)∈Rh×d是隐藏层的权重参数。运行中间变量后 z∈Rh通过激活函数 ϕ我们获得了长度的隐藏激活向量h,
(5.3.2)h=ϕ(z).
隐藏层输出h也是一个中间变量。假设输出层的参数只具有权重W(2)∈Rq×h,我们可以获得一个输出层变量,其向量长度为q:
(5.3.3)o=W(2)h.
假设损失函数是l示例标签是 y,然后我们可以计算单个数据示例的损失项,
(5.3.4)L=l(o,y).
根据定义ℓ2我们稍后将介绍的正则化,给定超参数λ,正则化项是
(5.3.5)s=λ2(‖W(1)‖F2+‖W(2)‖F2),
其中矩阵的 Frobenius 范数就是ℓ2将矩阵展平为向量后应用范数。最后,模型在给定数据示例上的正则化损失为:
(5.3.6)J=L+s.
我们指的是J作为下面讨论中的目标函数。
5.3.2. 前向传播的计算图
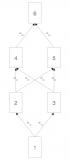
绘制计算图有助于我们可视化计算中运算符和变量的依赖关系。图 5.3.1 包含与上述简单网络相关的图形,其中方块表示变量,圆圈表示运算符。左下角表示输入,右上角表示输出。请注意箭头的方向(说明数据流)主要是向右和向上。
图 5.3.1前向传播计算图。
5.3.3. 反向传播
反向传播是指计算神经网络参数梯度的方法。简而言之,该方法根据微 积分的链式法则以相反的顺序遍历网络,从输出层到输入层。该算法存储计算某些参数的梯度时所需的任何中间变量(偏导数)。假设我们有函数 Y=f(X)和Z=g(Y), 其中输入和输出 X,Y,Z是任意形状的张量。通过使用链式法则,我们可以计算导数 Z关于X通过
(5.3.7)∂Z∂X=prod(∂Z∂Y,∂Y∂X).
在这里我们使用prod运算符在执行必要的操作(例如转置和交换输入位置)后将其参数相乘。对于向量,这很简单:它只是矩阵-矩阵乘法。对于更高维的张量,我们使用适当的对应物。运营商 prod隐藏所有符号开销。
回想一下,具有一个隐藏层的简单网络的参数,其计算图如图 5.3.1所示,是 W(1)和W(2). 反向传播的目的是计算梯度 ∂J/∂W(1)和 ∂J/∂W(2). 为此,我们应用链式法则并依次计算每个中间变量和参数的梯度。计算的顺序相对于前向传播中执行的顺序是相反的,因为我们需要从计算图的结果开始并朝着参数的方向努力。第一步是计算目标函数的梯度J=L+s关于损失期限 L和正则化项s.
(5.3.8)∂J∂L=1and∂J∂s=1.
接下来,我们计算目标函数相对于输出层变量的梯度o根据链式法则:
(5.3.9)∂J∂o=prod(∂J∂L,∂L∂o)=∂L∂o∈Rq.
接下来,我们计算关于两个参数的正则化项的梯度:
(5.3.10)∂s∂W(1)=λW(1)and∂s∂W(2)=λW(2).
现在我们可以计算梯度了 ∂J/∂W(2)∈Rq×h 最接近输出层的模型参数。使用链式规则产生:
(5.3.11)∂J∂W(2)=prod(∂J∂o,∂o∂W(2))+prod(∂J∂s,∂s∂W(2))=∂J∂oh⊤+λW(2).
获得关于的梯度W(1)我们需要继续沿着输出层反向传播到隐藏层。关于隐藏层输出的梯度 ∂J/∂h∈Rh是(谁)给的
(5.3.12)∂J∂h=prod(∂J∂o,∂o∂h)=W(2)⊤∂J∂o.
由于激活函数ϕ按元素应用,计算梯度 ∂J/∂z∈Rh中间变量的z要求我们使用逐元素乘法运算符,我们用⊙:
(5.3.13)∂J∂z=prod(∂J∂h,∂h∂z)=∂J∂h⊙ϕ′(z).
最后,我们可以得到梯度 ∂J/∂W(1)∈Rh×d 最接近输入层的模型参数。根据链式法则,我们得到
(5.3.14)∂J∂W(1)=prod(∂J∂z,∂z∂W(1))+prod(∂J∂s,∂s∂W(1))=∂J∂zx⊤+λW(1).
5.3.4. 训练神经网络
在训练神经网络时,前向传播和反向传播相互依赖。特别是,对于前向传播,我们沿依赖方向遍历计算图并计算其路径上的所有变量。然后将这些用于反向传播,其中图上的计算顺序是相反的。
以前述简单网络为例进行说明。一方面,在前向传播过程中计算正则化项(5.3.5) 取决于模型参数的当前值W(1)和W(2). 它们由优化算法根据最近一次迭代中的反向传播给出。另一方面,反向传播过程中参数(5.3.11)的梯度计算取决于隐藏层输出的当前值h,这是由前向传播给出的。
因此在训练神经网络时,在初始化模型参数后,我们交替进行正向传播和反向传播,使用反向传播给出的梯度更新模型参数。请注意,反向传播会重用前向传播中存储的中间值以避免重复计算。结果之一是我们需要保留中间值,直到反向传播完成。这也是为什么训练比普通预测需要更多内存的原因之一。此外,这些中间值的大小大致与网络层数和批量大小成正比。因此,使用更大的批量大小训练更深的网络更容易导致内存不足错误。
5.3.5. 概括
前向传播在神经网络定义的计算图中顺序计算和存储中间变量。它从输入层进行到输出层。反向传播以相反的顺序顺序计算并存储神经网络中中间变量和参数的梯度。在训练深度学习模型时,正向传播和反向传播是相互依赖的,训练需要的内存明显多于预测。
5.3.6. 练习
假设输入X一些标量函数 f是n×m矩阵。梯度的维数是多少f关于X?
向本节中描述的模型的隐藏层添加偏差(您不需要在正则化项中包含偏差)。
画出相应的计算图。
推导前向和反向传播方程。
计算本节中描述的模型中训练和预测的内存占用量。
假设您要计算二阶导数。计算图会发生什么变化?您预计计算需要多长时间?
假设计算图对于您的 GPU 来说太大了。
您可以将它分区到多个 GPU 上吗?
与在较小的 minibatch 上进行训练相比,优缺点是什么?
审核编辑黄宇
Discussions
-
pytorch
+关注
关注
2文章
808浏览量
13249
发布评论请先 登录
相关推荐
解读多层神经网络反向传播原理




 PyTorch教程-5.3. 前向传播、反向传播和计算图
PyTorch教程-5.3. 前向传播、反向传播和计算图













评论