Inductor-1---电感的模型参数
引言:电感器是与电阻R和电容器C并列的重要的被动元器件,有时也将其称作线圈。 通常,线圈是指呈环形的导线绕组,电路中的线圈是指电感器。 电感器的符号通常使用“L”来表示。 此举,是为了纪念物理学家俄国物理学家海因里希·楞次(Heinrich Lenz)。 电感器的基本结构为将导线缠绕成线圈状的,能够将电能转换成磁能并蓄积在电感器内部。 被蓄积的磁能量多少由电感器的电感值来决定,电感值的单位为亨利(H)。
1.电感的等效模型
理想的电感器,完全不含电感以外的成分,没有能量损耗。 但实际的电感器上除了电感以外还包含有电阻成分(直流电阻:DCR)和静电电容(分布电容:Cp),如图1-1模型所示。 电阻是绕组和磁芯具有的电阻成分,静电电容主要是绕组的线间电容。
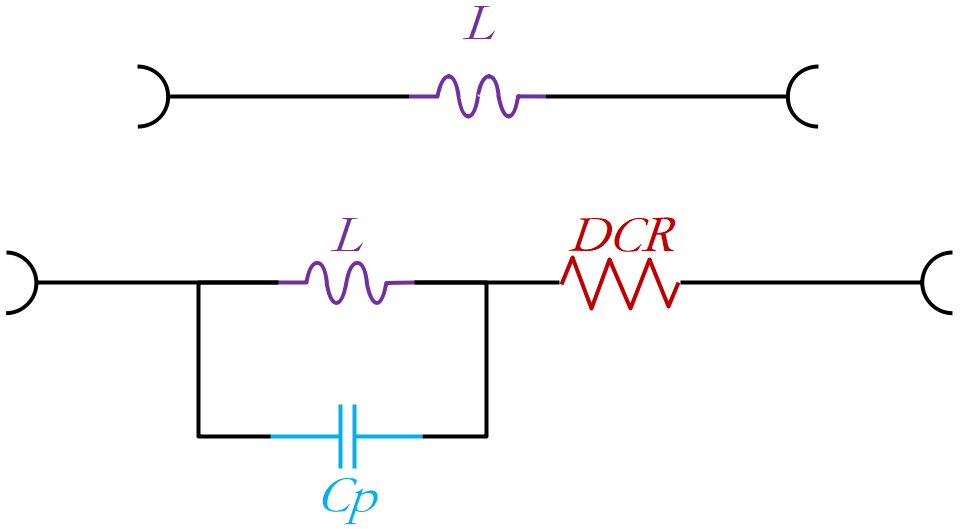
图1-1:理想电感和等效电感模型
2.电感的自共振特性
自共振,电感具有自共振的现象非常常见,因为从上述模型(图1-1)可以看到电感模型近似于一个并联RLC,对于并联RLC,一个重要的特性是阻抗。 简单地说,阻抗即为交流电路中的电压与电流之比,相当于直流电路中的电阻。 符号使用Z,单位与电阻相同,使用Ω。 电感器的阻抗Z由下面的计算过程导出:
电感部分会产生感抗:
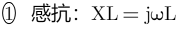
寄生电容Cp会产生容抗:
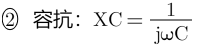
感抗和容抗相加:
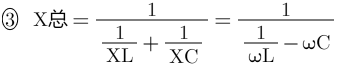
整理上式变为下式:
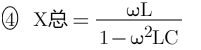
感容抗加上寄生电阻DCR合并为阻抗Z:
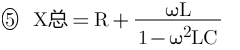
代入频率参数为:
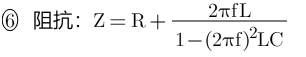
推导出:
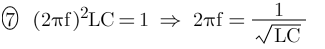
其中:
Z:阻抗(Ω)
R:直流电阻成分DCR(Ω)
j:虚数
ω:ω=2πf
f:频率(HZ)
L:电感(H)
C:杂散电容Cp(F)
根据上述公式拟绘出理想的电感器与实际的电感器相对于频率的阻抗特性示意 图1-2 。 理想的电感器,阻抗会随着频率的升高而呈线性增加。 但实际的电感器则会因分布电容而产生自共振现象,在更高的频率下阻抗下降,不再作为本来的电感器发挥作用。 此外,还因电阻成分或阻抗的下降而产生损耗。
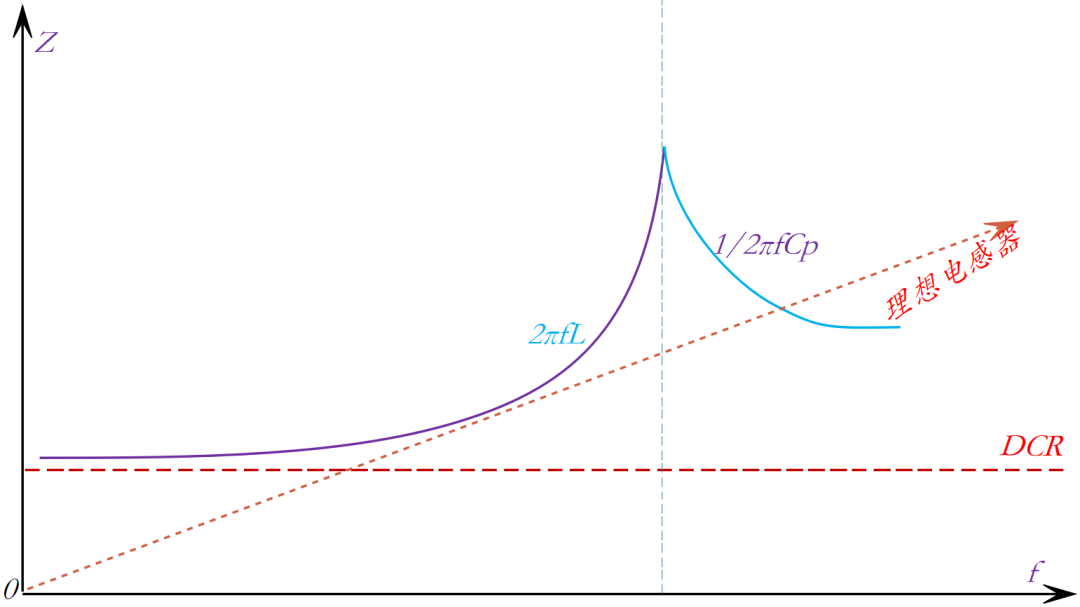
图1-2:实际电感阻抗曲线
并且从式7可以看出,任何数除以0都是无穷大,对应此时f处的阻抗为无穷大,正好对应曲线图1-2处的尖峰阻抗点,此点即为共振点。 回顾Capacitor-1:电容的模型和参数由此得出:电容的自谐振点阻抗最低,而电感的自共振点阻抗最高。
3.电感的工作原理
电感器基本工作原理如下:
(1) 当线圈中有电流通过时,线圈的周围就会产生磁场。 当线圈中电流发生变化时,其周围的磁场也产生相应的变化。
(2) 将电能转变为磁能并蓄积起来。
(3) 直流会流过,但交流不易流过,频率越高越不易流过。
(1)和(2)是基于电感器的电磁感应的特性。 (3)是电感器“阻交流,通直流”的特性。 这里就如何利用这些特性,列出各自的具体例子。
例一:当线圈中有电流通过时,线圈的周围就会产生磁场。 当线圈中电流发生变化时,其周围的磁场也产生相应的变化。 ⇒变压器的原理,图1-3一次侧和二次侧具有两个绕组的构造中,可以认为与变压器一样。 如果让交流电流向一次侧绕组,变压器铁芯产生交变磁场,在该磁场的作用下,次级线圈就产生感应电动势。 这是因为电磁感应而引起的,若是变压器时则称之为互感。 通过变压器的线圈的匝数比等于电压比,将一次侧绕组和二次侧绕组转换成任意的电压。
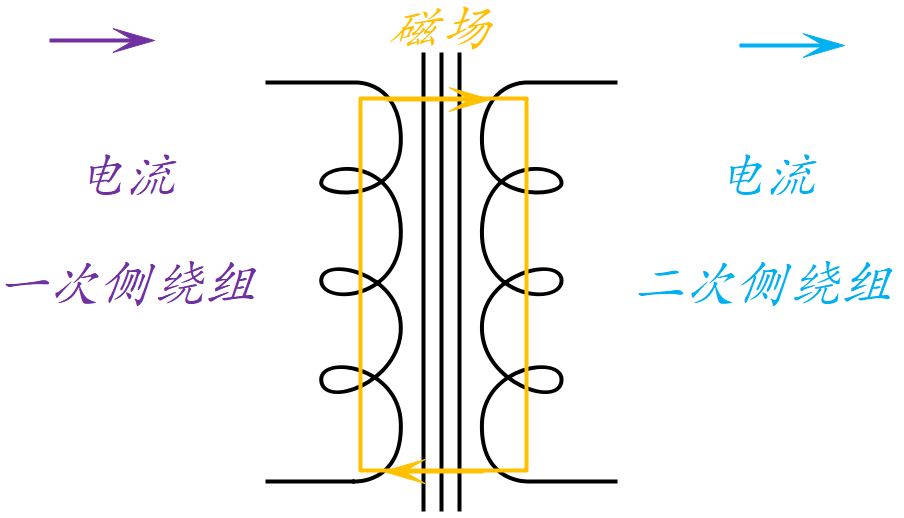
图1-3:变压器模型
例二:根据楞次定律,将电能转换为磁能并蓄积起来⇒扼流圈的原理,这里列出的是DC/DC转换器的电感器示例(DC-DC-2:降压型的工作原理; DC-DC-3:升压型的工作原理)。 如果将开关置于ON而让电流流向电感器,就会产生磁场,电感器上就会以磁能的形式将能量蓄积起来。 如果将开关置于OFF而停止流向电感器的电流,之前被蓄积起来的磁能就会释放(磁场发生变化),电流就会流过。 这也是因为电磁感应而引起的,若是以单独的绕组构成的电感器时则称之为自感,不带隔离的DC-DC器件基本都是使用自感型电感器。
例三:直流会流过,但交流不易流过,频率越高越不易流过⇒滤波器的作用,可通过借助阻抗因频率而发生变化,利用交流不易流过的特性,如图1-4与电容器组合来构成低通滤波器和高通滤波器等,关于阻抗的特性将在后面描述。
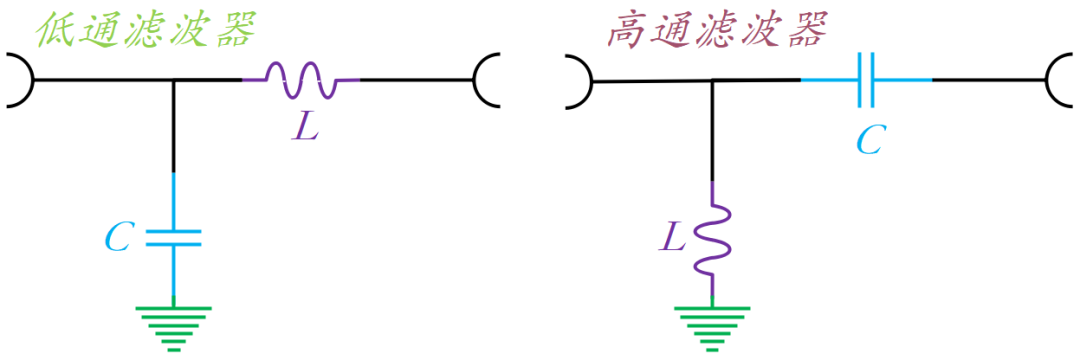
图1-4:电感与电容组成的简易无源滤波器
4.电感与电容的比较
根据上述说明,将电感器的特点与电容器进行对比而归纳成下表。 如表1-1中所示,电感器具有与电容器正好相反特性。
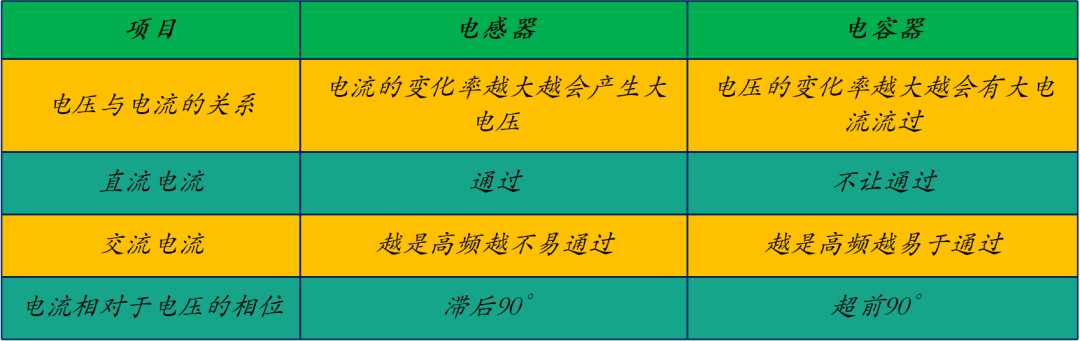
表1-1:电感和电容比较
-
电容器
+关注
关注
64文章
6213浏览量
99466 -
线圈
+关注
关注
14文章
1818浏览量
44399 -
电感器
+关注
关注
20文章
2326浏览量
70475 -
RLC
+关注
关注
1文章
116浏览量
38905 -
等效模型
+关注
关注
0文章
14浏览量
6365
发布评论请先 登录
相关推荐
射频电感器的选择参数
电感器的选择
射频电感器选型的关键参数是什么?
射频电感器选择参数知多少?
射频电感器如何选型_射频电感器的五大选型参数介绍

射频电感器应该如何选择参数

电感器结构的原理及电感器基础知识的分享
贴片功率电感厂商科普功率电感器参数及选型要求 gujing






 电感器的模型和参数
电感器的模型和参数
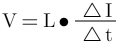










评论