量子扩散如何实现更大尺度独立集问题的求解

考虑一个社交网络，用网络中的顶点代表人，网络中的边代表两人互相认识，而网络中一群相互认识的人，我们可以用一个由相应顶点两两连接构成的子图表示，并称之为团。如果想知道一个社交网络中有哪些共同朋友的群体以及其中最大的群体是哪个，我们该如何搜索寻找呢？这便是著名的最大团问题（Maximum Clique Problem），它属于一类NP难（NP-hard）问题。在计算复杂度理论中，如果求解一个问题的时间T随输入大小n呈多项式增长，即T(n) = O(nk)，则称该问题为Polynomial复杂度问题，即P问题，这类问题容易求解。如果一个问题的解可以在多项式时间内被猜测和验证，则该问题称为 Nondeterministic Polynomial复杂度问题，简称NP问题，Nondeterministic意味着没有可遵循的特定规则来猜测该问题的解，一般认为不存在精确算法可以高效求解它。著名的整数质因子分解就是一个NP问题。NP难问题本身不是NP问题，但是如果任何一个NP难问题被证明是一个P问题，那么所有的NP问题就一定是P问题，即P=NP。（目前P=NP并未得到证明，且多数人相信P≠NP。）在图论中，最大团问题可用于社交网络分析，以识别具有共同兴趣、爱好或信仰的人群，除此之外，最大团问题在计算化学、生物信息学等领域也有诸多应用。

最大团问题或团问题可以等价地转化为无向图上的独立集问题（Independent Set Problem）。它描述的是一个无向图中那些由两两不相邻的顶点所组成的集合。对于一张由V个顶点，E条边构成的图G(V, E)，它的某一个独立集S是由图中若干顶点组成的，且要求S中任意两个顶点之间没有边的连接，每一个独立集所包含的顶点数目被定义为该独立集的基数，其中基数最大的独立集则称之为图G(V, E)的最大独立集。由于无向图中的一个团同时也是该无向图补图中的一个独立集，因此最大独立集问题与最大团问题在计算复杂度上是相互等价的。（在图论中，补图是指将原图中相邻边删去，不相邻边连接后形成的图。）

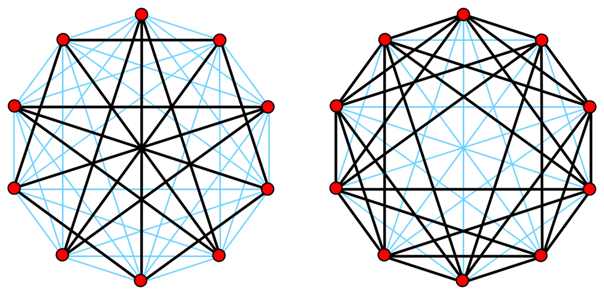
图2：十顶点彼得森图（左侧）及其补图（右侧）

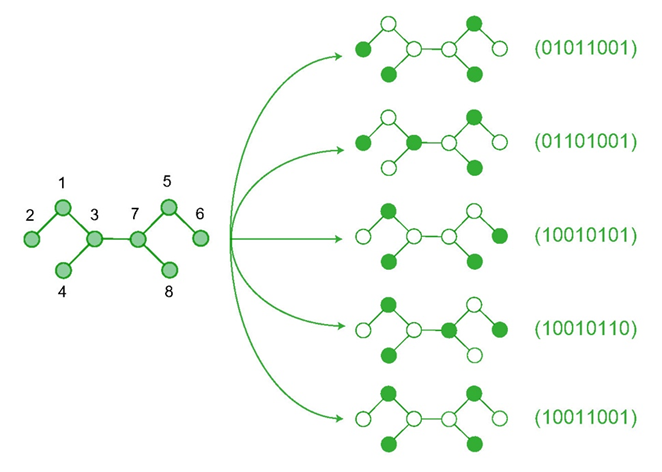
图3：图G(8,7)的5个最大独立集

以图3中图G(8, 7)为例，我们将不属于独立集的空心点用二进制数0来表示，将属于独立集的实心点用二进制数1来表示，经过计算我们发现实心点个数最多为4个，例如图中的5种最大独立集（图3中右侧所示），可用8位二进制数表示。解决独立集问题或最大独立集问题在经济学、生物学、计算机视觉等领域有着广泛的应用。目前对于线图、平面图、树图等典型结构，寻找它们所有的最大独立集是一个Polynomial复杂度问题, 即P问题，可以用经典算法高效解决。然而，对于一般图，枚举或者计算其最大独立集数量已经被证明是NP难问题[1]。因此，计算机科学家们的普遍共识是：不存在精确求解一般图最大独立集问题的高效算法。因此如何利用量子计算的优势高效寻找一般图中的独立集，并进一步探索其最大独立集的问题是一个非常有趣和重要的问题。最近人们发现求解独立集问题可以自然地映射为一类求解哈密顿量基态的问题，然后利用量子绝热演化来获得基态。而随着实验威廉希尔官方网站 的不断发展，操控量子系统作绝热演化已经成为可能[2-3]。

绝热量子计算

在过去的几十年里，由于量子绝热算法在解决一般基态问题方面比经典算法具有潜在的加速能力，因此人们付出了巨大的努力来设计和扩展量子绝热算法的能力，这些算法在计算化学、材料科学、机械制造等领域有着广泛的应用。

绝热量子计算的基本思想是：首先设计一个目标哈密顿量HP使得它的基态是我们所感兴趣的问题的解（它是未知的因此无法直接制备）。然后，我们再设计一个简单的哈密顿量HB，它的基态不但已知而且实验上易于制备。在实验中，我们将系统初始化为哈密顿量HB而且让其处于基态。接下来，通过施加外场的方式驱动该简单哈密顿量HB作绝热演化，使其缓慢演化为目标哈密顿量HP。根据绝热量子理论，系统在绝热演化过程中将会一直保持在基态，所以当演化结束后，系统所处的最终状态即为目标哈密顿量HP的基态，这正是该问题的解。

图4：系统的含时哈密顿量H(t)。t为时间参量，初始时t为0，演化结束时t为1。

绝热量子计算的时间复杂度是指完成绝热演算所需的时间，与哈密顿量的本征能隙有关。具体地说，如果系统处于基态，在绝热演化过程中，基态与第一激发态之间的能隙Δ将给出系统演化速度的上界，当Δ越小时，系统的演化速度就越慢。整个算法的运行时间可以被约束为：

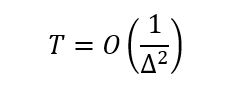
这里Δ代表H(t)的最小能缝，如图5所示。

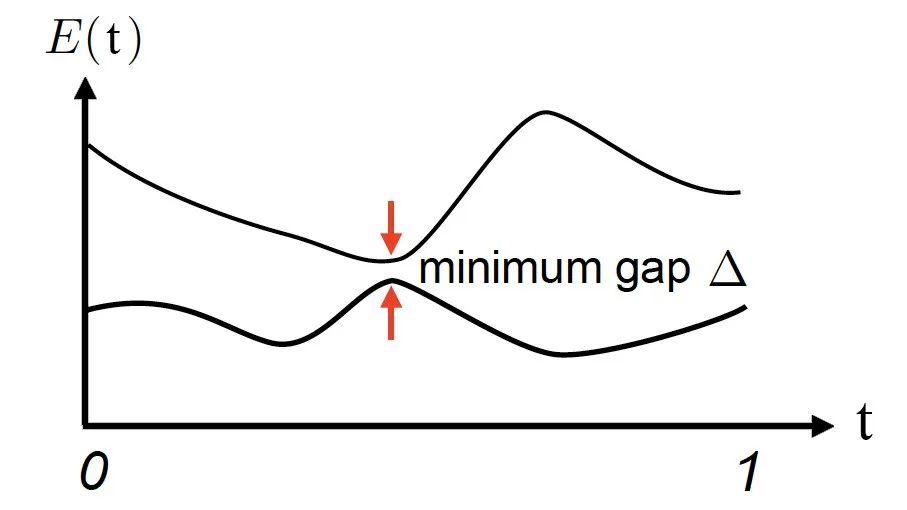
图5：绝热演化过程中系统能量E(t)随时间t的演化

虽然上述传统的由HB到HP的绝热演化方案简单且常用，但如何选择合适的初始哈密顿量HB使得能隙Δ尽量大仍是一项具有挑战性的任务。对于大多数的选择，能隙Δ会随系统大小n指数减小，这样得到的量子绝热算法是指数慢的，和相应的经典算法比没有优越性。

幸运的是，对于独立集问题，我们可以成功地避开这个困难。对应图G(V, E)，我们构建如下多体哈密顿量其目标哈密顿量，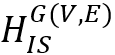

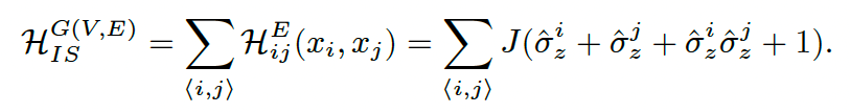这个哈密顿量的基态是简并的，它们和图G(V, E)的独立集一一对应。有别于传统的绝热演化方案，我们将哈密顿量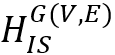同时设置为初始和目标哈密顿量，在绝热演化中每一个自旋缓慢旋转。由于基态简并，系统在演化中会等效地感受到一个非阿贝尔规范势（Non-Abelian Gauge Field）或非阿贝尔贝里联络（Non-Abelian Berry Connection）。这样一来，一个初始的易于制备的系统基态（如直积态|0〉⊗n）将演化成为包含哈密顿量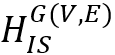所有基态（对应独立集问题所有解）的相干叠加态∑an|gn〉，最后，我们通过量子投影测量读出这个波函数中包含的解的信息，从而解决相应的独立集问题。这便是我们最近实验工作中用于求解独立集问题的量子算法的基本演算流程。 我们称这个与传统的绝热演化算法不同的方法为非阿贝尔绝热量子混合算法[4]，在解决独立集问题上的它具有两个独特优势：（1）在绝热演化过程中，系统基态和第一激发态之间的能隙Δ是一个保持不变的常数4J，其中J是一个描述系统中两体相互作用耦合强度的基本参数。换句话说，我们算法中的能隙Δ与待求解的独立集问题G(V, E)的大小和结构均无关，这就确保了我们的算法具有一个恒定的运行时间，而且这比解决独立集问题中态制备和读出的时间短很多。（2）驱动哈密顿量演化只需要局部的幺正操作即可（例如绕固定轴的单比特旋转操作），这大大降低了实验中对量子系统的操控难度，使得利用可调线性光学量子线路来演示非阿贝尔绝热量子混合算法也是可行的。 量子扩散

从物理图像上看，非阿贝尔绝热混合过程可以等效看作一个粒子在高维中值图中的量子扩散现象[4]。对于一个图G(V, E)，中值图里的顶点是它的独立集，当且仅当两个独立集之间的汉明距离（Hamming distance）为一时，两个顶点之间会有实线相连。为了更明确地阐明这种量子扩散过程，我们以代表性图G(8, 7)为例，可以看到系统最初被制备在一个简单的基态|g0〉上，在八维中值图中我们用中心的黑点来表示（图6左上图）。在系统绝热演化过程中，系统初态逐渐演化为中间哈密顿量的基态，对应于八维中值图中心的黑点逐渐向四周扩散的过程，同时也是独立集问题的解开始在希尔伯特空间中自然“涌现”的过程，这里黑点和蓝点分别代表正确的基态，而红色和空心点代表错误的基态（图6右图）。最后，随着系统哈密顿量重新回到初始时的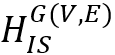，系统的基态最终演化为哈密顿量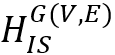所有基态的相干叠加，对应于八维中值图中的扩散结束，所有代表错误解的红点消失，而代表正确解的黑点和蓝点以大致相等的概率分布在八维中值图中（图6左下图）。

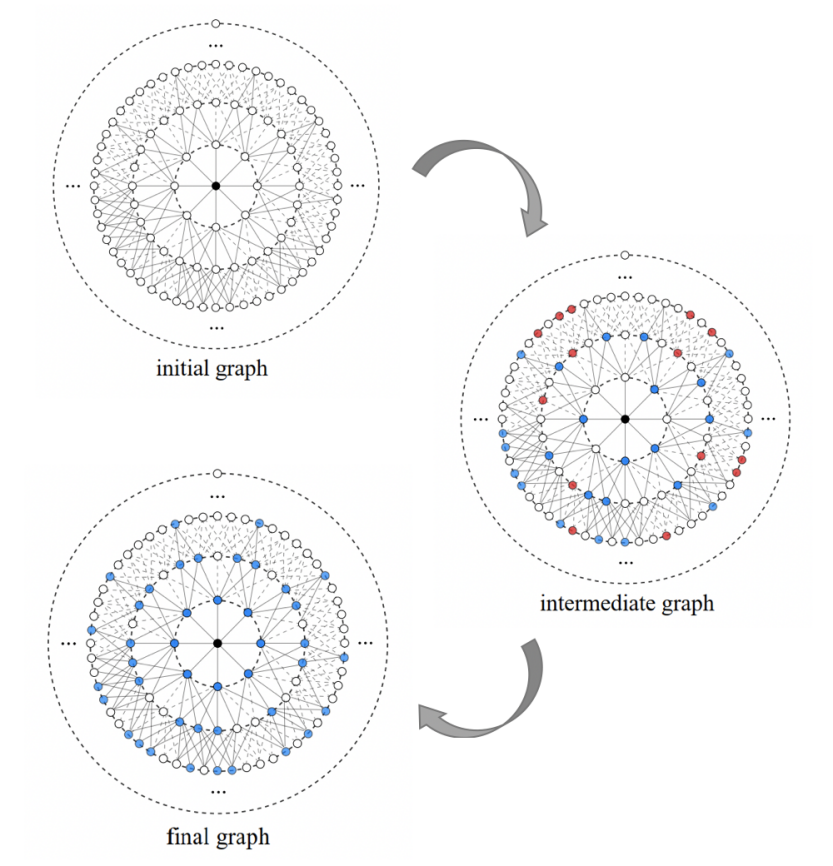
图6：八维中值图中的量子扩散过程

基于上述理论模型，中国科大潘建伟、陈宇翱、姚星灿等与北京大学吴飙、美国麻省理工学院Frank Wilczek合作，首次在线性光学量子线路中演示了非阿贝尔绝热量子混合算法，并成功求解了若干个独立集问题，其中对图G(8, 7)的求解成功概率达到了87.5%，非平庸解占比达到31.4%。实验中还观测到量子态在高维中值图空间中的量子扩散过程，为利用非阿贝尔绝热混合算法解决具有内禀非阿贝尔规范对称性的组合优化问题铺平了道路，相关成果最近刊登在了《美国国家科学院院刊》（PNAS）[5]。

未来，研究者们还会继续改进现有的绝热量子算法模型[6]，尝试提高最大独立集和非平庸独立集的求解概率，通过降低系统噪声来压制得到错误解的概率，并进一步探索在离子、原子等其他物理系统中实现更大尺度独立集问题的求解，在NISQ时代为量子计算解决特定复杂问题提供新的思路和开辟新的道路。