文章讨论了如何实现最佳的温度传感器精度。它讨论了两个物体之间的热流源和速率,然后解释和计算了温度误差的来源。最后,它提出了减少热误差和优化温度测量的设计理念。MAX1298/MAX1299 ADC内置温度传感器。
MAX1298/MAX1299模数转换器带有内部温度传感器,在扩展温度范围内(-1°C至40°C)具有保证±85°C的精度,是业界任何器件在该范围内最佳的温度传感器精度。本文解释了如何在使用热和机械系统的情况下实际达到这种精度水平。
MAX1298/MAX1299的典型内部温度误差与温度的关系如图1所示。要达到这种精度水平,需要仔细注意系统设计的热和机械方面。
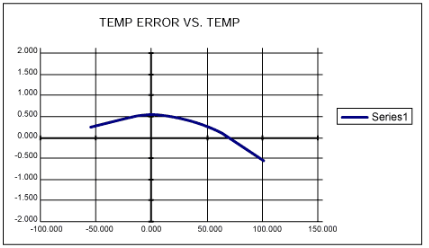
图1.MAX1298/MAX1299的内部温度误差与温度(°C)的关系
由于MAX1298/MAX1299的封装必须与要测量温度的物体(OM)进行机械和热连接,如果器件与被测物体之间存在温差,则它们之间将存在热流。另外,由于MAX1298/MAX1299温度传感器(TS)的封装必须机械和热连接到电源(PS),因此,如果MAX1298/MAX1299与PS之间存在温差,它们之间将存在热流。如果MAX1298/MAX1299与周围环境(AE)之间存在温差,它们之间也会有热流。
热“集总”系统的定义如下:
由导热材料互连的系统,导热材料在径向方向上是隔热的,这意味着导体径向方向的电导率与其沿其长度的电导率相比非常低(绝缘铜线就是一个例子),或
通过导热硅“润滑脂”互连的系统。
热集总系统中任何两个物体之间的热流速率可以表示为:
(dQ/dt)12 = (T1- T2) × K × A12/(x2-x1) Joules/sec
在上式中,T1和 T2分别是物体 1 和物体 2 的温度(以 °C 为单位),K 是互连材料的热导率 [以焦耳/(°C × 米 × 秒为单位)],A12是互连材料的横截面积(以米²为单位),(x2 - x1)是互连材料的长度(以米为单位)。有关各种材料的导热系数(K)值,请参见下表。
| 材料 | K (J/(m × 的× °C) |
| 银 | 420 |
| 铜 | 380 |
| 金 | 290 |
| 硅散热器化合物 | 0.75 |
等式1可以简化为:
(dQ/dt)12 = (T1- T2) × K12 Joules/sec
在这个方程中,K12是物体 1 和物体 2 之间互连的特定热导率,单位为焦耳/(°C × 秒)。
估算MAX1298/MAX1299温度传感器与周围环境之间的热导率(KTSAE)涉及更多,因为从我们的2cm×2cm温度传感器(TS)PC板到周围环境(AE)的辐射并不是真正的热集总过程,而更像是一个热分布过程。你可以估计 K上汽假设 PC 板实际上是黑体散热器。这允许使用Stefan-Boltzmann公式,该公式仅使用散热器的表面积(A)和两个温度的四次方TTS和 TAE:
KTSAE = A × 56.697 × (TTS 4 - TAE 4) × 10-9 J/sec
现在,为了简化起见,让我们假设被测对象、电源和周围环境充当大型储热器,以便在它们之间交换热量时它们的温度不会改变。请注意,对于MAX1298/MAX1299温度传感器,我们不能做出这样的假设,因为它的尺寸和质量都很小。现在,我们可以使用电气原理图作为interwetten与威廉的赔率体系 来制作系统的热模型(见图2)。
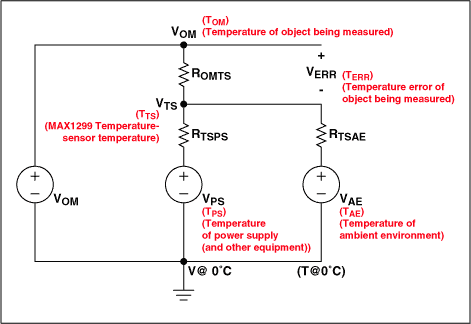
图2.热系统的电气模拟。
ROMTS表示被测物体的储热器(VOM)和温度传感器之间的热阻。ROMTS的热阻为1/KOMTS。同样,RTSPS表示温度传感器和电源储热器(VPS)之间的热阻。RTSPS的热阻为1 / KTSPS。最后,RTSAE表示温度传感器和环境环境储热器(VAE)之间的热阻。RTSAE的热阻为1 / KTSAE。现在假设温度传感器本身不会产生任何热量。然后请注意,温度传感器 (TTS) 处的温度类似于温度传感器节点上的电压 VTS。我们可以将其计算为各种组件的函数:
VTS = (VOM × KOMTS + VPS × KTSPS + VAE × KTSAE)/(KOMTS + KTSPS + KTSAE)
现在,让我们通过在 VOM 和 TOM 之间选择 1:1 的关系来让我们的生活更轻松。因此,让VOM = TOM (°C),VPS = TPS (°C),VAE = TAE (°C)。
例如,让我们使TOM = 75°C,TPS = 30°C和TAE = 25°C,因此VOM = 75V,VPS = 30V,VAE = 25V。
为了找到 K 项的值,让我们做出以下假设:
KOMTS是由于在温度传感器PC板和被测物体之间施加了1mm厚,20mm x 20mm面积的硅散热器化合物。常用硅胶散热器化合物的 K 值为 18 × 10-4 Cal/(°C × cm × sec) = 0.75 J/(°C × m × sec)。因此:
KOMTS = 0.75 × (0.02 × 0.02)/1 × 10-3 = 0.3 焦耳/(°C × 秒)
KTSPS由4米长、16根导体(假设MAX1298/MAX1299上的所有引脚都使用)、π ×(1mm)²的绝缘铜电缆横截面积构成。(这是一根 16 芯 4 米长的 1mm 半径铜缆。这些电缆大多具有圆形而不是方形导体,因此π × r²面积项。MAX1298引脚非常短,因此它们的贡献微不足道。然后
KTSPS = 380 焦耳/(米 × 秒 × °C) × (16 × π × (1 × 10-3m)²)/4m = 0.0048 焦耳/(°C × 秒)
KTSAE是由于20mm x 20mm的印刷电路板直接连接到周围环境。根据等式 3,KTSAE = (0.02 × 0.02) × 56.697nW/meter²/°C4 × (TTS 4 - TAE 4)。如果我们假设硅散热器化合物两端的热压降相对较小,那么TTS~TOM和
KTSAE ~ (0.02m × 0.02m) × 56.697 × 10(-9 × (TOM 4 - TAE 4) = 709uJ/(°C × 秒)
现在将K项的计算值和我们上面选择的电压值代入,我们得到以下结果:
VTP = (75 × 0.3 + 30 × 0.0048 + 25 × 0.000709)/(0.3 + 0.0048 + 0.000709) = 74.177V
最后,我们考虑MAX1298/MAX1299在最大功率下工作的情况,看看这对TERR有什么影响。MAX1298/MAX1299的最大功率 = 5.5V × 500μA = 2.75mW。在TERR方程中对该项的一个很好的估计是在TERR项中添加一个增量TERR,使得TERR增量为~2.75mW/KOMTS = 2.7 × 10-3/0.3 = 9 × 10-3 °C ~ + 0.01°C。 因此,在此设置中,可以安全地忽略MAX1298/MAX1299对TERR的贡献。
在本例中,我们发现温度传感器的温度为 74.177°C。温度误差 TERR = TTS - TOM = 74.177 - 75.000 = -0.823°C。 这是一个相当大的误差,但由于它取决于各种温度,因此可能会更高或更低。为了观察这一点,取公式4并用其相关温度替换电压:
TTP = (TOM × KOMTS + TPS × KTSPS + TAE × KTSAE)/(KOMTS + KTSPS + KTSAE)
因此:
TERR = TTS - TOM = [(TOM × KOMTS + TPS × KTSPS + TAE × KTSAE)/(KOMTS + KTSPS + KTSAE)] - TOM
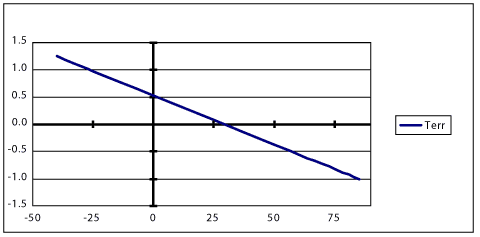
该系统的TERR与TOM曲线如图3所示。
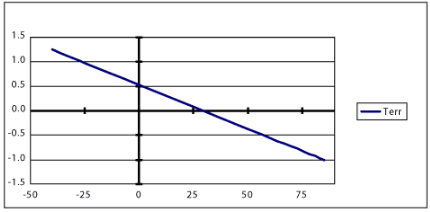
图3.TERR (°C) vs. TOM (°C).
如图3所示,系统热特性引起的温度误差可能大于MAX1298/MAX1299温度传感器引起的误差。可以做几件事来帮助减少此错误 (T犯 错):
减少电源(和其他处于环境温度的设备)和温度传感器之间的导体数量。这可以通过不使用MAX1298/MAX1299提供的所有功能来实现。
增加温度传感器 PC 板尺寸。未与MAX1298/MAX1299电连接并覆盖电路板两侧的金属平面,如果将其紧紧拧入被测物体,则会增加KTSOM。MAX1298/MAX1299应位于印刷电路板的被测对象侧。
加长将温度传感器连接到电源(以及处于或接近环境温度的其他设备)的导体。这可以通过在电缆的电源端附近卷起多余的电线来实现。电缆的电源端的温度低于温度传感器端的温度,因此从额外绝缘体辐射出的任何“径向”热量都将具有较小的ΔT驱动它。注意,MAX1298/MAX1299电源需要在温度传感器PCB上具有本地电容去耦,因为电缆中存在大量串联电感。
通过备用通道(如光隔离器或光纤电缆)传输数字信号。该交替通道串行数据可以在温度传感器上本地恢复。这将有助于减少所需的导体数量(见上面的数字1)。
用电池为MAX1298/MAX1299供电。这与上面的数字3相结合,原则上可以完全消除导体并使T犯 错微不足道。由于MAX1298/MAX1299具有许多关断选项,因此这是一个可行的选择。
从上面的例子可以看出,对于高精度温度测量系统,在设计电气和机械部件期间以及理想情况下在设计之前考虑设计的热方面至关重要。
审核编辑:郭婷
-
传感器
+关注
关注
2550文章
51065浏览量
753296 -
温度传感器
+关注
关注
48文章
2940浏览量
156046 -
隔离器
+关注
关注
4文章
773浏览量
38325
发布评论请先 登录
相关推荐
Maxim高精度6通道温度传感器MAX6689
MAX9924–MAX9927性能及应用
Maxim具有最高精度的可编程温度监视器MAX6689
低成本高精度传感器信号调理器MAX1452相关资料下载
MAX1298,MAX1299, MAX1298A,MAX1
MAX6694 带有beta补偿的5通道高精度温度监测器
Using MAX1298/MAXAchieving Hig
MAX1299CEAE+ MAX1299CEAE+ - (Maxim Integrated) - 温度传感器 - 模拟和数字输出

MAX1298CEAE+T MAX1298CEAE+T - (Maxim Integrated) - 温度传感器 - 模拟和数字输出

MAX1299CEAE+T MAX1299CEAE+T - (Maxim Integrated) - 温度传感器 - 模拟和数字输出

MAX1298CEAE+ MAX1298CEAE+ - (Maxim Integrated) - 温度传感器 - 模拟和数字输出





 使用MAX1298/MAX1299温度传感器实现高精度
使用MAX1298/MAX1299温度传感器实现高精度










评论