LDPC码在IEEE802.16e、IEEE802.11n、IEEE802.11ac、IEEE802.11ad以及5G等高吞吐量系统中得到了广泛的应用。
信道编解码作为整个通信系统中最难实现的一部分,众多高校、研究院所、企业,投入了大量的人力资源进行研究与实现。
在信道编解码威廉希尔官方网站 中,译码主要分为硬判决译码和软判决译码。
LDPC硬判决译码算法主要分为:消息传递(Message-Passing,MP)算法、比特翻转(Bit Flipping, BF)算法和Gallager A、B算法。比特翻转算法中,先求取HCT,如果为0则停止译码,否则翻转参与校验失败校验方程最多的变量节点对应的比特,再计算HCT,如此迭代直到HCT=0或达到设定迭代次数。Gallager A、B算法算法过程参考其博士论文。硬判决译码性能较差,使用软判决可显著提高译码性能。
LDPC软判决译码基于置信度传播(BP)算法(或叫做和积SP算法),通过在变量节点VN和校验节点CN之间传播和更新置信度信息来达到译码收敛的效果。通过BP算法,又衍生出最小和算法,以及归一化最小和算法,偏置最小和算法。
一切算法研究,需要从脑海理论到落地实践,通过仿真验证,再到工程应用,才能将知识转变为财富。
01
MP译码算法
消息传递(MP)算法是迭代解码算法,在VN和CN之间来回传递消息,直到进程停止。消息标记的Mi表示已知bit值为0或1,e表示已删除位。
在LDPC译码中,用Bj符号表示H的奇偶校验方程中的bit集合(每一行中1的位置集合),用Ai符号表示码的第i位的奇偶校验方程(每一列中1的位置集合)。
考虑下面的奇偶校验矩阵:
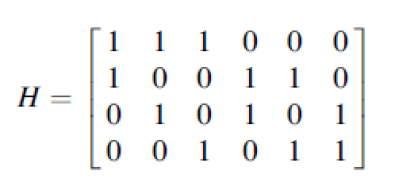
对于上面的奇偶校验矩阵,我们得到:
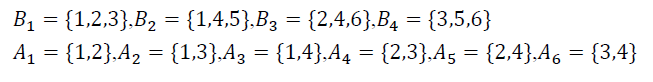
基于(Binary Erasure Channel,BEC)的LDPC译码处理过程如下:

02
BF译码算法
收到符号硬解码成1和0组成一个二进制向量y。在每个迭代中,计算所有检查和,以及涉及每一个n bit向量y不满足奇偶检验的数量。接下来,如果y的比特包含最大数量的未满足奇偶校验,则将其翻转。该过程将重复进行,直到所有校验和都满足或达到预定的迭代次数。
比特翻转译码算法的步骤如下:

03
BP(SP)算法
和积算法类似于前一节中描述的比特翻转算法,但表示每个判决(无论位值是1还是0)的消息现在都是概率。比特翻转译码接受接收比特的初始硬判定作为输入,和积算法是接受接收位的概率作为输入的软判定消息传递算法。在LDPC译码器操作之前,输入信道或接收比特的概率是已知的,因此它们也被称为接收比特的先验概率。在和积解码器中,节点之间传递的外部信息也是概率。校验节点j与比特节点i之间的外部信息用Eji表示; Eji给出了bit ci为1时使奇偶校验方程j满足的概率。如果第i位不包含在j中,则无法定义Eji,因为在检查节点j和第i bit之间没有外部信息。
奇偶校验方程中奇数个bit 是1的概率是:
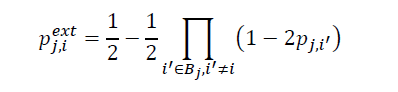
也就是bit ci为1时奇偶校验方程满足的概率。bit ci为0时满足奇偶校验方程的概率为
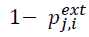
二元变量的度量用以下对数似然比(LLR)表示:
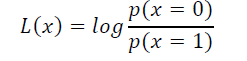
其中,log就是loge,L(x)符号提供了x的硬判决,并且模|L(x)|决定了判决的可靠性。将LLR转化为概率:
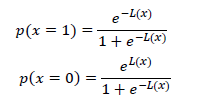
当需要将概率相乘时,只需要加LLR,从而降低和积译码器的复杂性。这使得概率的对数表示有了好处。从校验节点j 到比特节点i
到比特节点i 的外部信息表示为LLR:
的外部信息表示为LLR:
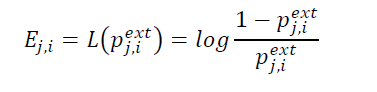
从而有:
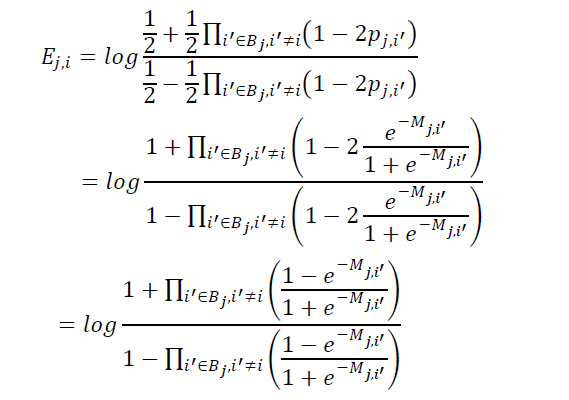
其中:
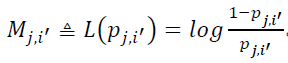
运用关系式
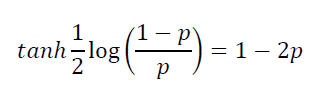
于是得到:
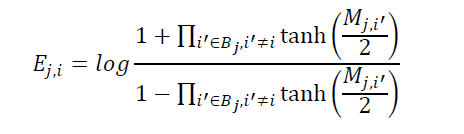
或者,运用关系式
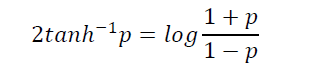
则有
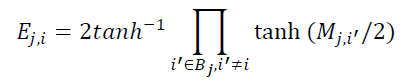
由于存在tanh和tanh-1函数的乘积,上述方程在数值上具有挑战性。
考虑Mj,i'其符号和大小(或bit值和bit可靠性):
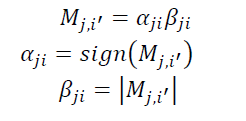
于是有
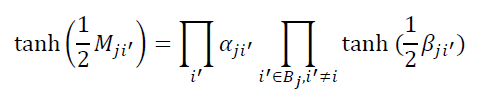
然后我们可以得到:
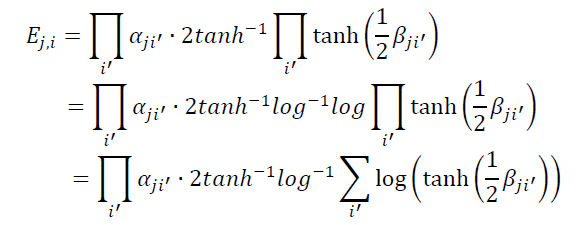
上式产生了一种新的形式:
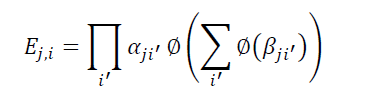
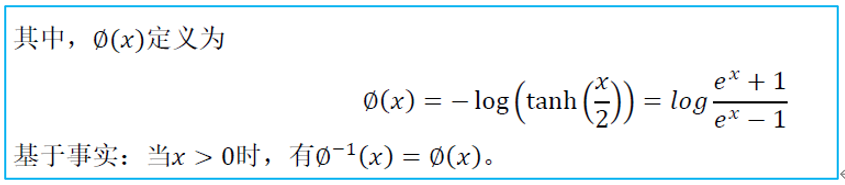
每个比特节点都可以连接输入LLR,Li,以及每个连接的检查节点的LLR。第i位的总LLR就是这些LLR的和:
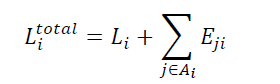

对于所有的j,i,有Hj,i=1。因此,yi代表实际接收到的信道值,即不是有效值。对于不同的信道,Li可以计算:
BEC:
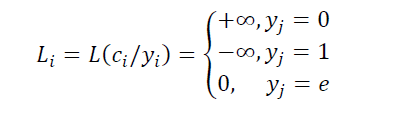
BSE:
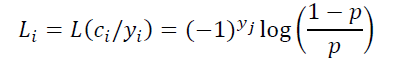
BI-AWGNC:

瑞利信道:

对数域和积译码算法总结如下:


04
Min-Sum算法
Min-Sum算法是对数域和积译码算法的简化,主要考虑到和积译码算法在硬件实现上的复杂性,进而采用了一种近似算法。

归一化最小和译码算法的实现采用分层置信传播算法,是对上式(4-26)的修正,乘一个取值范围0~1的缩放因子。
偏置最小和译码算法,则是在归一化最小和译码算法的基础上,减去一个偏置因子。
审核编辑:刘清
-
解码器
+关注
关注
9文章
1140浏览量
40706 -
LDPC
+关注
关注
1文章
66浏览量
31187 -
5G
+关注
关注
1354文章
48401浏览量
563791 -
5G通信
+关注
关注
4文章
242浏览量
20319 -
LDPC译码
+关注
关注
0文章
2浏览量
1101
原文标题:5G通信算法:LDPC译码算法详解
文章出处:【微信号:HXSLH1010101010,微信公众号:FPGA威廉希尔官方网站 江湖】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
FPGA-5G通信算法的基本套路
什么是Turbo 码的迭代译码算法?当前Turbo译码算法有哪些?有哪些形式的Turbo 码?
IEEE 802.16e中LDPC译码器的实现
基于LDPC译码软信息的迭代载波恢复
准循环LDPC码的两种典型快速译码算法研究
LDPC编译码

近地应用CCSDS标准LDPC码动态补偿译码算法研究

对LDPC码的LLR BP算法研究
非规则LDPC码译码改进算法概述及DSP的实现分析

求解LDPC码回路的算法
如何使用软件无线电实现NR LDPC编译码的设计与实现





 5G通信算法:LDPC译码算法详解
5G通信算法:LDPC译码算法详解










评论