大家对电机的认识可能就是高中课本里的交变电流章节的例子,电刷+外磁场+通电线圈。这是最经典的有刷电机。但是今天咱们谈论的是另一种更高效、性能更好的电机——无刷电机。
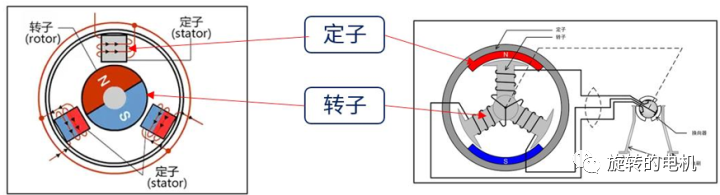
如图是无刷电机的等效模型。内外两个灰色的轮子一个是定子,一个是转子(具体哪个是定子哪个是转子根据电机类型有所不同)。此时转子和定子是完全重合在一起的,没有扭矩的存在。
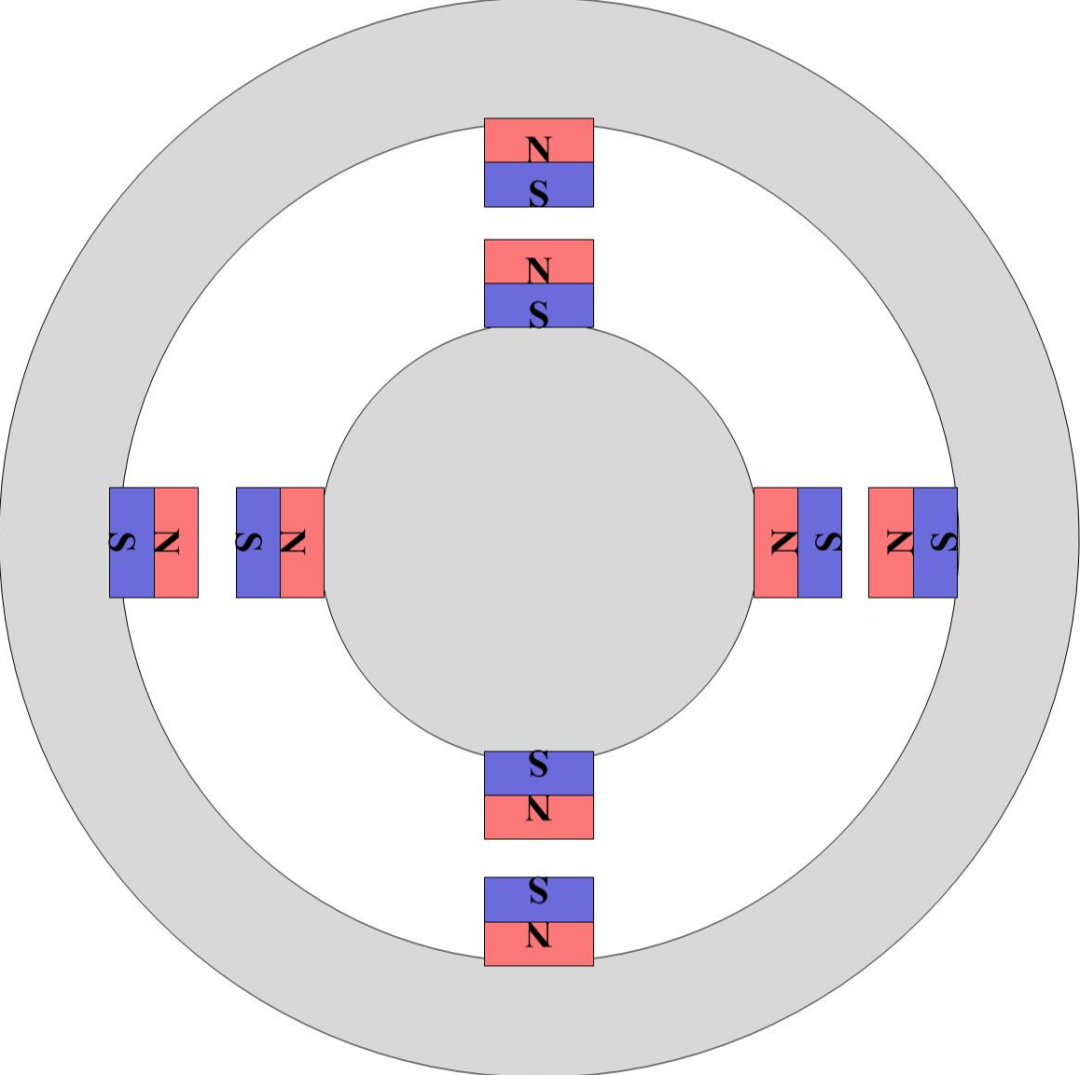
咱们定性地看,当外部的定子磁场扭转一个角度时,内部的转子会跟着旋转。这个时候就存在扭矩了。
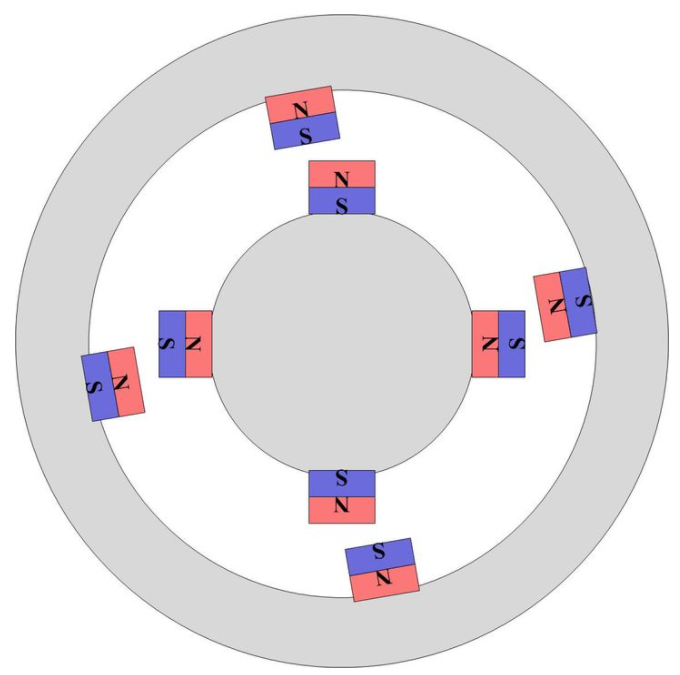
扭矩的大小如何衡量?如下图所示
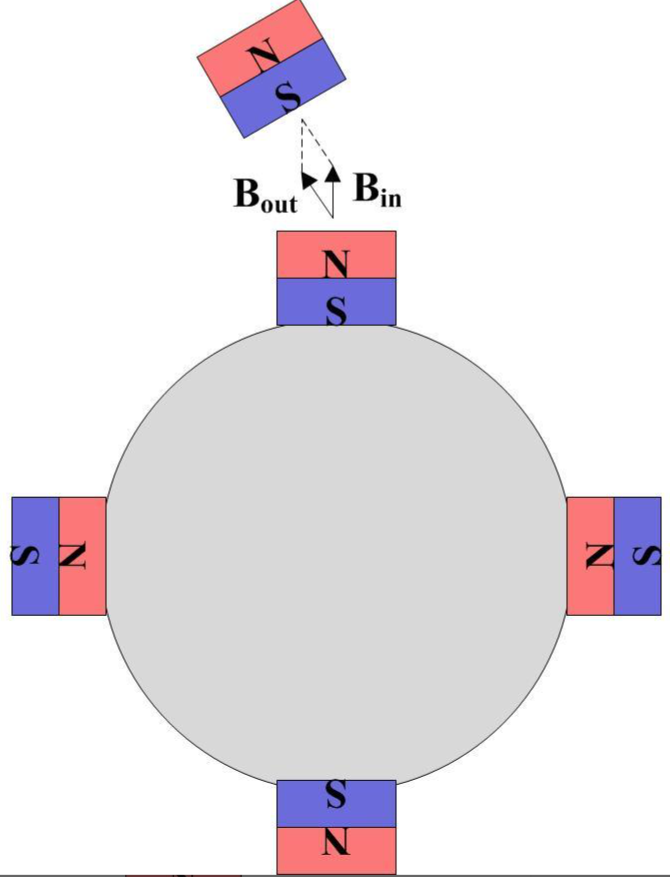
所有的电机扭矩的大小正比于内外两个磁场的叉乘,即图中围出的平行四边形的面积。可见两个磁场重合时,叉乘为0,扭矩也为0,和之前的直观认知相符合。显然,当两个磁场呈90度时,平行四边形面积最大,此时的扭矩也最大。
实际的无刷直流电机(BLDC)或永磁同步电机(PMSM)通常用三相****交流绕组线圈充当定子,永磁体作为转子。我们希望通过电路控制定子绕组的输出,使之能够能产生一个大小尽可能恒定的旋转磁场,让转子和定子的扭矩达到最大值。
( 具体为何使用三相线圈的相应电路分析笔者在此不予赘述 )
这就是FOC(Field-Oriented Control)矢量控制要完成的目标
FOC(Field-Oriented Control),即磁场定向控制,也称矢量变频,是近几年较为主流的高效控制无刷直流电机(BLDC)和永磁同步电机(PMSM)的选择。
要实现这样的功能,我们可以简单分为以下分为两步
- 如何产生一个可控的旋转磁场
- 如何让这个磁场大小稳定
如何产生一个可控的选择磁场
要得到一个恒定大小的旋转磁场很容易。当今主流的BLDC和PMSM电机定子均采用的是三相绕组,即各个绕组上的交流信号就是相位互差120°的信号。根据三相电机的结构,我们可以 将一个恒定大小的旋转电压矢量分解到相位互差120°的方向上 。如下图
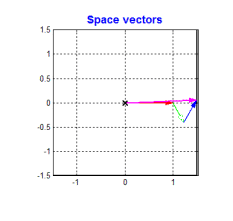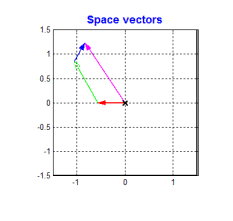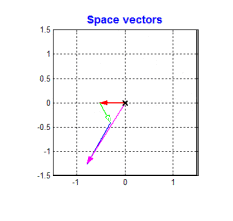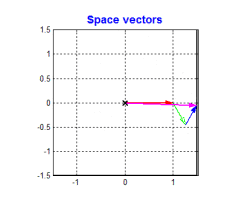
从上图可以看到,只要控制电机的三个绕组产生相位互差120°的大小随着时间按正弦规律变化的3个分矢量,就可以得到我们想要的旋转磁场
如何让磁场大小稳定
然而,在实际的电机控制中,由于齿槽效应、磁通畸变等因素,电机的转矩会产生大量的波动,需要不断地对控制信号做出修正。但是当电机转速较高时,电流环控制器必须跟踪频率不断提高的弦波信号,而且还要克服振幅和频率不断提高的电机反电动势。在这样的情况下,想要直接通过维持三路正弦信号得到旋转平滑、大小稳定并且一直保持和转子磁场方向垂直的磁场难以实现。
我们重新回到一开始的磁场叉乘。我们发现电机的转矩 只与 平行于内磁场方向(称d轴)的磁场分量 和 垂直于内磁场方向的分量(称q轴) 有关(如下图)。
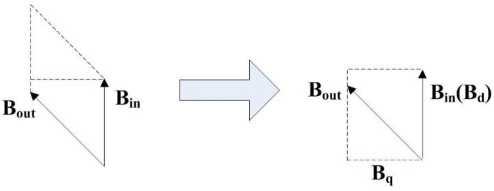
现在对于电机扭矩大小的控制就变成了q轴和d轴大小乘积的控制。在电机中,d轴上内磁场的大小是永磁铁产生的,是恒定的;我们对外磁场的控制实质上变成了q轴上的分量大小控制+外磁场的角度。
我们可以使用编码器测量转子的内磁场角度,然后根据内磁场的角度用电机绕组产生对应的外磁场。
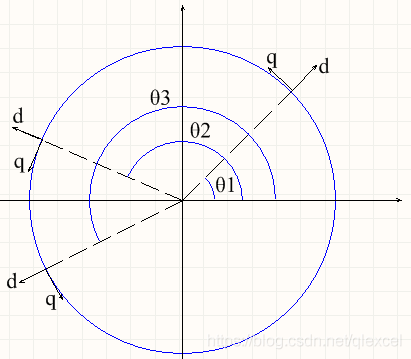
如上图所示,如果转子的电角度在θ1,则我们就要在θ1处产生d、q轴大小的外磁场。如果转子的电角度在θ2,则我们就要在θ2处产生d、q轴大小的外磁场。
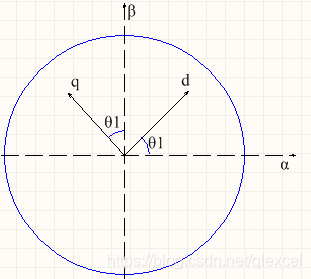
我们把角度θ1的情况单独提出来,把它移到原点去,然后把x、y轴重命名为α,β。根据空间矢量的关系,我们可以把q、d轴的大小分解到α,β轴上。这个过程就是所谓的“反 帕克(Park)变换 ”。
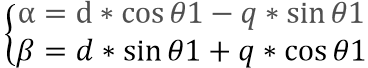
若d=0
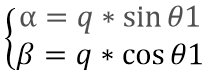
其实得到的结果很简单,它就是用了互差90°的正弦信号得到了大小恒定的旋转磁场。
控制电机只需要4步:
第一步,选定q、d轴的值(比如q=2,d=0)。
第二步,用编码器测量转子电角度(内磁场角度)。
第三步,用上面的式子计算α,β值。
第四步,把α,β输入到专门的处理电路SVPWM,输出三相信号驱动电机
(对SVPWM的介绍可以参考这篇CSDN文章。
http://t.csdn.cn/bFZZc
可以大概理解为在PWM输出的基础上增加若干花里胡哨的风骚处理( ̄▽ ̄)~*)
绕了这么多弯弯,我们终于让电机转起来了。大家看到这里可能会说:“这是在折腾啥?(╬ ̄皿 ̄)不还是最后转成三个相差120°的正弦信号了吗?”
(* ̄︶ ̄)
没错,到目前为止只是在绕弯子。但是关键在于下面几个问题:
1、我怎么知道电机有没有按照我设定的q、d值来转呢?
2、设定q、d值只能控制扭矩,我如果要控制电机的速度和位置怎么办?
这些问题都是上面那个开环系统解决不了的,这个时候就要引入闭环了。
我们先测量电机的3相电流。电机的信号如下图所示(把相差120°的电信号看成同一个旋转向量在三个相差120°坐标轴上的投影)
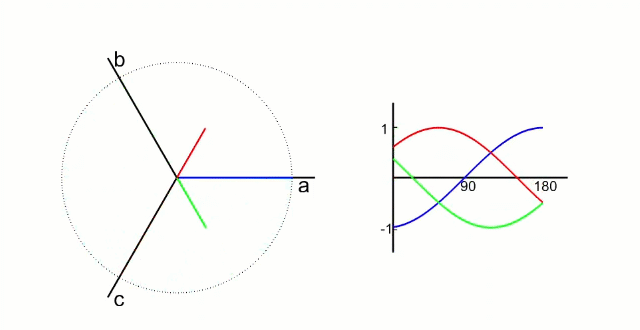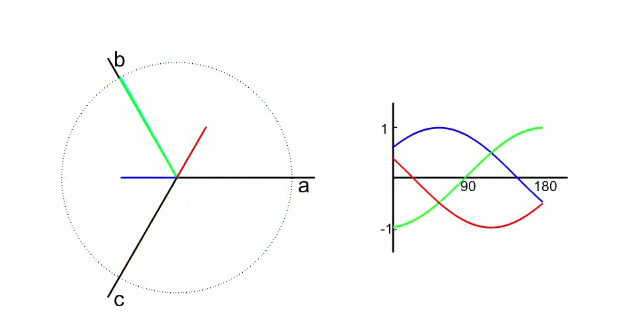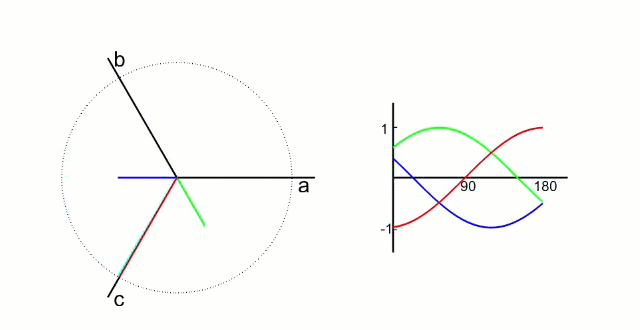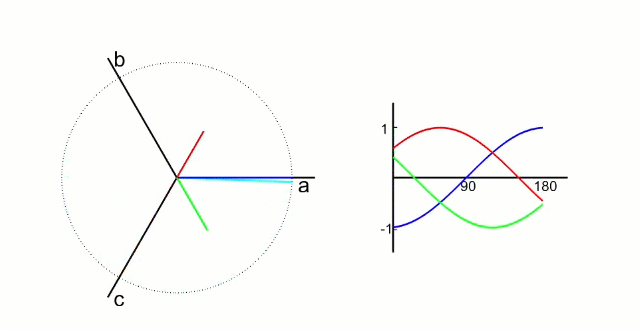
根据我们之前的理论,我们需要的是两个互差90°的磁场。这里咱们又使用一个变换,把三个分磁场变换成α、β方向上的两个分磁场。这个叫做“ 克拉克(Clarke)变换 ”。
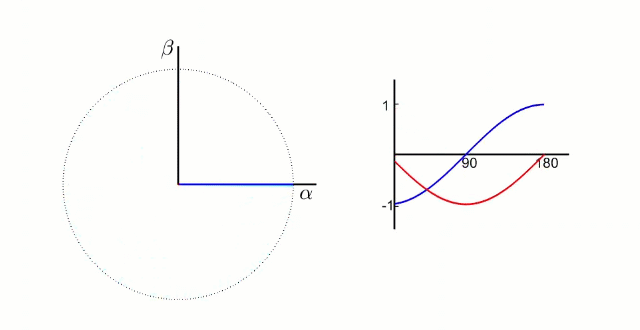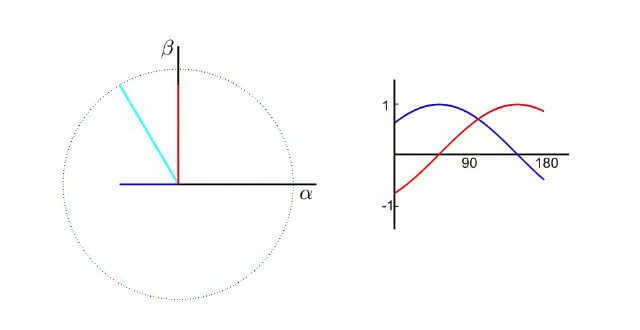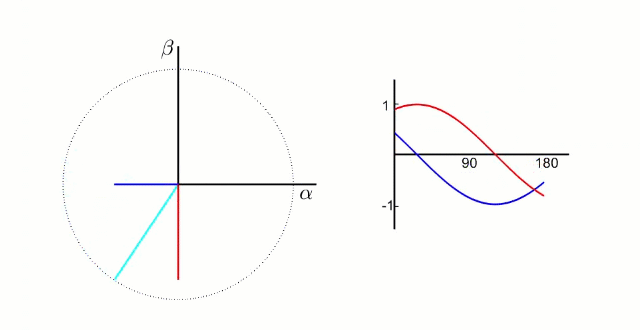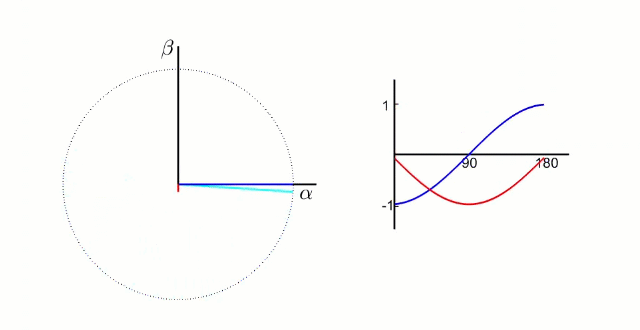
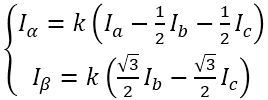
(变换中有一个系数k,一般取2/3,有兴趣可以去搜索了解)
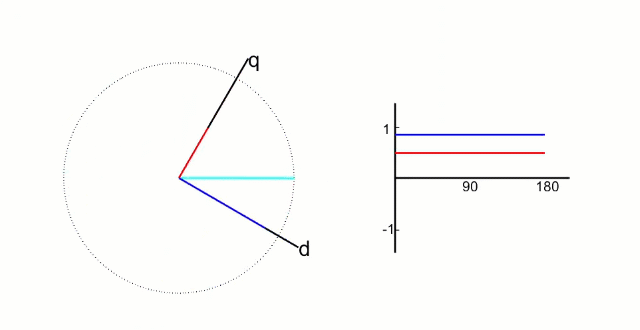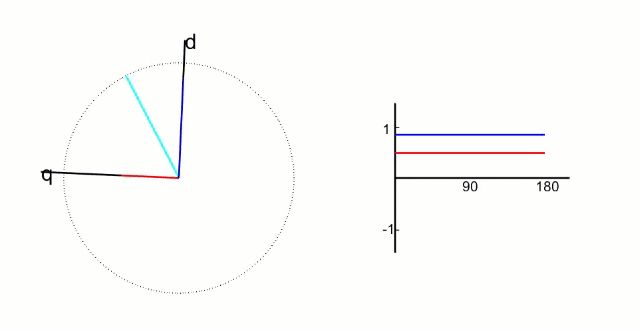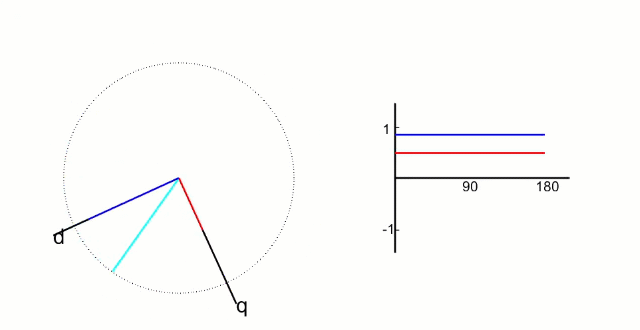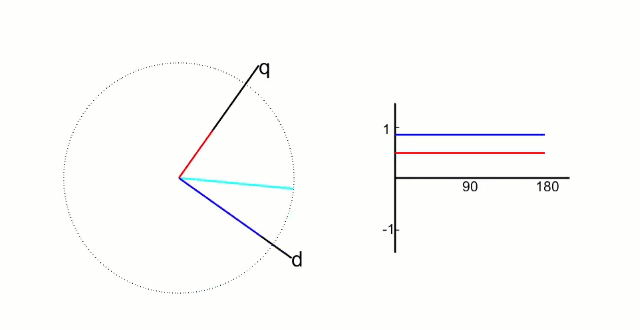
再把α,β轴上的值映射到旋转的q、d轴上,得到此时电机实际的d值和p值。这是之前反Park变换的逆过程, “ 帕克Park变换”
我们把测量到的d、q轴值与我们设定的值做对比,通过PI算法消除误差,再重新通过之前的流程输入到SVPWM中,这就完成了一个闭环控制,可以对定子磁场的做动态修正了。因为控制d、q是在控制电流值,所以这个环路叫做电流环。
总结一下,电流环的逻辑是这样的
- 设置d0、q0值(目标值),经过反Park变换得到Iα和Iβ,输入给SVPWM执行
- 测量q、d轴的值:测量电机的相电流(测量两相,通过Ia+Ib+Ic=0得到第三相),然后通过Clarke变换得到Iα和Iβ,然后通过park变换得到q、d轴的值。
- 把测量到的d、q轴值与我们设定的d0、q0做对比,进行PID处理。(目标是让测量值与我们的设定值相同)
- 调整d、q值输出,回到1.
除了电流环之外,由于d、q是直流信号, 我们通过d、q也可以更轻松地控制电机的 转速和旋转位置 。
比如设定电机转速为1000Rpmin,编码器测得当前转速为500,同样用PID算法增大q值就可以加大扭矩,让电机的速度加快了。这个环路叫 速度环, 即在电流环的外面加一层,改变q、d设定值来改变速度。
当然我们也可以加上 位置环 ,通过对速度的积分可以得到电机的位置,计算位置误差进行PID调整。
看ヾ(✿゚▽゚)ノ,我们把对三相交流正弦信号的控制转换成了对直流信号d,p的控制,这样优势就出来了,很nice~
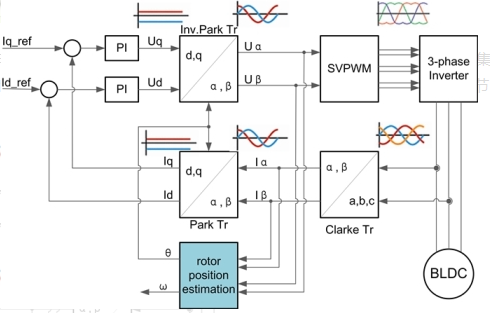
FOC控制简图
其他
除了FOC之外,还有其他控制电机的方法,比如梯形波式控制、弦波控制等。详细介绍可以参考这篇文章
http://t.csdn.cn/7UsSi
简单概括,弦波式换相能让电机在低速下运转平稳,但在高速运转下效率却大大降低;而梯形波式换相在电机高速运转下工作比较正常,但在电机低速运转下,会产生力矩的波动。因此,矢量控制是对无刷电机的最佳控制方式~
-
磁场
+关注
关注
3文章
877浏览量
24212 -
电机
+关注
关注
142文章
9010浏览量
145415 -
无刷电机
+关注
关注
57文章
839浏览量
45833
发布评论请先 登录
相关推荐
直流无刷电机的工作原理的详细资料简介
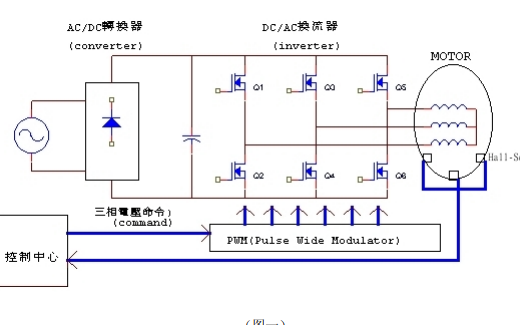




 无刷电机的工作原理与扭矩
无刷电机的工作原理与扭矩












评论