我以前的文章主要都是讲解算法的原理和解题的思维,对时间复杂度和空间复杂度的分析经常一笔带过,主要是基于以下两个原因:
1、对于偏小白的读者,希望你集中精力理解算法原理。如果加入太多偏数学的内容,很容易把人劝退。
2、正确理解常用算法底层原理,是进行复杂度的分析的前提。尤其是递归相关的算法,只有你从树的角度进行思考和分析,才能正确分析其复杂度。
鉴于现在历史文章已经涵盖了所有常见算法的核心原理,所以我专门写一篇时空复杂度的分析指南,授人以鱼不如授人以渔,教给你一套通用的方法分析任何算法的时空复杂度。
本文会篇幅较长,会涵盖如下几点:
1、Big O 表示法的几个基本特点。
2、非递归算法中的时间复杂度分析。
3、数据结构 API 的效率衡量方法(摊还分析)。
4、递归算法的时间/空间复杂度的分析方法,这部分是重点,我会用动态规划和回溯算法举例。
废话不多说了,接下来一个个看。
Big O 表示法
首先看一下 Big O 记号的数学定义:
O(g(n))= {f(n): 存在正常量c和n_0,使得对所有n ≥ n_0,有0 ≤ f(n) ≤ c*g(n)}
我们常用的这个符号O其实代表一个函数的集合,比如O(n^2)代表着一个由g(n) = n^2派生出来的一个函数集合;我们说一个算法的时间复杂度为O(n^2),意思就是描述该算法的复杂度的函数属于这个函数集合之中。
理论上,你看明白这个抽象的数学定义,就可以解答你关于 Big O 表示法的一切疑问了 。
但考虑到大部分人看到数学定义就头晕,我给你列举两个复杂度分析中会用到的特性,记住这两个就够用了。
1、只保留增长速率最快的项,其他的项可以省略 。
首先,乘法和加法中的常数因子都可以忽略不计,比如下面的例子:
O(2N + 100) = O(N)
O(2^(N+1)) = O(2 * 2^N) = O(2^N)
O(M + 3N + 99) = O(M + N)
当然,不要见到常数就消,有的常数消不得:
O(2^(2N)) = O(4^N)
除了常数因子,增长速率慢的项在增长速率快的项面前也可以忽略不计:
O(N^3 + 999 * N^2 + 999 * N) = O(N^3)
O((N + 1) * 2^N) = O(N * 2^N + 2^N) = O(N * 2^N)
以上列举的都是最简单常见的例子,这些例子都可以被 Big O 记号的定义正确解释。如果你遇到更复杂的复杂度场景,也可以根据定义来判断自己的复杂度表达式是否正确。
2、Big O 记号表示复杂度的「上界」 。
换句话说,只要你给出的是一个上界,用 Big O 记号表示就都是正确的。
比如如下代码:
for (int i = 0; i < N; i++) {
print("hello world");
}
如果说这是一个算法,那么显然它的时间复杂度是O(N)。但如果你非要说它的时间复杂度是O(N^2),严格意义上讲是可以的,因为O记号表示一个上界嘛,这个算法的时间复杂度确实不会超过N^2这个上界呀,虽然这个上界不够「紧」,但符合定义,所以没毛病。
上述例子太简单,非要扩大它的时间复杂度上界显得没什么意义。但有些算法的复杂度会和算法的输入数据有关,没办法提前给出一个特别精确的时间复杂度,那么在这种情况下,用 Big O 记号扩大时间复杂度的上界就变得有意义了。
比如前文 [动态规划核心框架]中讲到的凑零钱问题的暴力递归解法,核心代码框架如下:
// 定义:要凑出金额 n,至少要 dp(coins, n) 个硬币
int dp(int[] coins, int amount) {
// base case
if (amount <= 0) return;
// 状态转移
for (int coin : coins) {
dp(coins, amount - coin);
}
}
当amount = 11, coins = [1,2,5]时,算法的递归树就长这样:
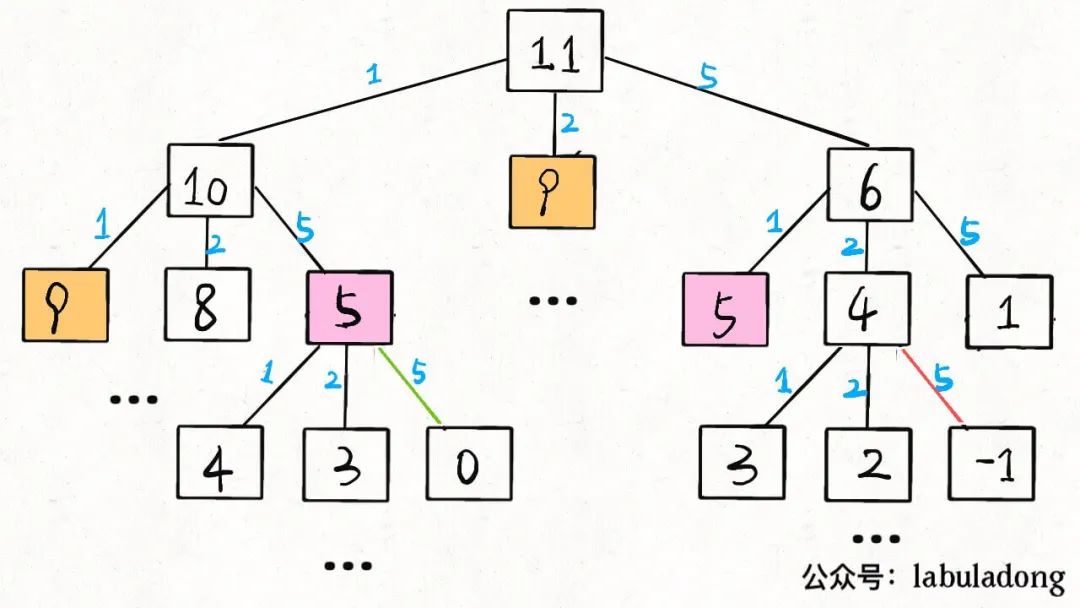
后文会具体讲递归算法的时间复杂度计算方法,现在我们先求一下这棵递归树上的节点个数吧。
假设金额amount的值为N,coins列表中元素个数为K,那么这棵递归树就是一棵K叉树。但这棵树的生长和coins列表中的硬币面额有直接的关系,所以这棵树的形状会很不规则,导致我们很难精确地求出树上节点的总数。
对于这种情况,比较简单的处理方式就是按最坏情况做近似处理:
这棵树的高度有多高?不知道,那就按最坏情况来处理,假设全都是面额为 1 的硬币,这种情况下树高为N。
这棵树的结构是什么样的?不知道,那就按最坏情况来处理,假设它是一棵满K叉树好了。
那么,这棵树上共有多少节点?都按最坏情况来处理,高度为N的一棵满K叉树,其节点总数为K^N - 1,用 Big O 表示就是O(K^N)。
当然,我们知道这棵树上的节点数其实没有这么多,但用O(K^N)表示一个上界是没问题的。
所以,有时候你自己估算出来的时间复杂度和别人估算的复杂度不同,并不一定代表谁算错了,可能你俩都是对的,只是是估算的精度不同 ,一般来说只要数量级(线性/指数级/对数级/平方级等)能对上就没问题。
在算法领域,除了用 Big O 表示渐进上界,还有渐进下界、渐进紧确界等边界的表示方法,有兴趣的读者可以自行搜索。不过从实用的角度看,以上对 Big O 记号表示法的讲解就够用了。
非递归算法分析
非递归算法的空间复杂度一般很容易计算,你看它有没有申请数组之类的存储空间就行了,所以我主要说下时间复杂度的分析。
非递归算法中嵌套循环很常见,大部分场景下,只需把每一层的复杂度相乘就是总的时间复杂度:
// 复杂度 O(N*W)
for (int i = 1; i <= N; i++) {
for (int w = 1; w <= W; w++) {
dp[i][w] = ...;
}
}
// 1 + 2 + ... + n = n/2 + (n^2)/2
// 用 Big O 表示化简为 O(n^2)
for (int i = 0; i < n; i++) {
for (int j = i; j >= 0; j--) {
dp[i][j] = ...;
}
}
但有时候只看嵌套循环的层数并不准确,还得看算法 具体在做什么 ,比如前文 [一文秒杀所有 nSum 问题] 中就有这样一段代码:
// 左右双指针
int lo = 0, hi = nums.length;
while (lo < hi) {
int sum = nums[lo] + nums[hi];
int left = nums[lo], right = nums[hi];
if (sum < target) {
while (lo < hi && nums[lo] == left) lo++;
} else if (sum > target) {
while (lo < hi && nums[hi] == right) hi--;
} else {
while (lo < hi && nums[lo] == left) lo++;
while (lo < hi && nums[hi] == right) hi--;
}
}
这段代码看起来很复杂,大 while 循环里面套了好多小 while 循环,感觉这段代码的时间复杂度应该是O(N^2)(N代表nums的长度)?
其实,你只需要搞清楚代码到底在干什么,就能轻松计算出正确的复杂度了 。
这段代码就是个 [左右双指针] 嘛,lo是左边的指针,hi是右边的指针,这两个指针相向而行,相遇时外层 while 结束。
甭管多复杂的逻辑,你看lo指针一直在往右走(lo++),hi指针一直在往左走(hi--),它俩有没有回退过?没有。
所以这段算法的逻辑就是lo和hi不断相向而行,相遇时算法结束,那么它的时间复杂度就是线性的O(N)。
类似的,你看前文 [滑动窗口算法核心框架]( 给出的滑动窗口算法模板:
/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
unordered_map<char, int> need, window;
for (char c : t) need[c]++;
// 双指针,维护 [left, right) 为窗口
int left = 0, right = 0;
while (right < s.size()) {
// 增大窗口
right++;
// 判断左侧窗口是否要收缩
while (window needs shrink) {
// 缩小窗口
left++;
}
}
}
乍一看也是个嵌套循环,但仔细观察,发现这也是个双指针技巧,left和right指针从 0 开始,一直向右移,直到移动到s的末尾结束外层 while 循环,没有回退过。
那么该算法做的事情就是把left和right两个指针从 0 移动到N(N代表字符串s的长度),所以滑动窗口算法的时间复杂度为线性的O(N)。
数据结构分析
因为数据结构会用来存储数据,其 API 的执行效率可能受到其中存储的数据的影响,所以衡量数据结构 API 效率的方法和衡量普通算法函数效率的方法是有一些区别的。
就拿我们常见的数据结构举例,比如很多语言都提供动态数组,可以自动进行扩容和缩容。在它的尾部添加元素的时间复杂度是O(1)。但当底层数组扩容时会分配新内存并把原来的数据搬移到新数组中,这个时间复杂度就是O(N)了,那我们能说在数组尾部添加元素的时间复杂度就是O(N)吗?
再比如哈希表也会在负载因子达到某个阈值时进行扩容和 rehash,时间复杂度也会达到O(N),那么我们为什么还说哈希表对单个键值对的存取效率是O(1)呢?
答案就是, 如果想衡量数据结构类中的某个方法的时间复杂度,不能简单地看最坏时间复杂度,而应该看摊还(平均)时间复杂度 。
比如说前文 [特殊数据结构:单调队列] 实现的单调队列类:
/* 单调队列的实现 */
class MonotonicQueue {
LinkedList
标准的队列实现中,push和pop方法的时间复杂度应该都是O(1),但这个MonotonicQueue类的push方法包含一个循环,其复杂度取决于参数e,最好情况下是O(1),而最坏情况下复杂度应该是O(N),N为队列中的元素个数。
对于这种情况,我们用平均时间复杂度来衡量push方法的效率比较合理。虽然它包含循环,但它的平均时间复杂度依然为O(1)。
计算平均时间复杂度最常用的方法叫做「聚合分析」,思路如下 :
给你一个空的MonotonicQueue,然后请你执行N个push, pop组成的操作序列,请问这N个操作所需的总时间复杂度是多少?
因为这N个操作最多就是让O(N)个元素入队再出队,每个元素只会入队和出队一次,所以这N个操作的总时间复杂度是O(N)。
那么平均下来,一次操作的时间复杂度就是O(N)/N = O(1),也就是说push和pop方法的平均时间复杂度都是O(1)。
类似的,想想之前说的数据结构扩容的场景,也许N次操作中的某一次操作恰好触发了扩容,导致时间复杂度提高,但总的时间复杂度依然保持在O(N),所以均摊到每一次操作上,其平均时间复杂度依然是O(1)。
-
API
+关注
关注
2文章
1499浏览量
61975 -
数据结构
+关注
关注
3文章
573浏览量
40124 -
递归
+关注
关注
0文章
28浏览量
9013 -
动态规划算法
+关注
关注
0文章
6浏览量
1625
发布评论请先 登录
相关推荐
如何降低LMS算法的计算复杂度,加快程序在DSP上运行的速度,实现DSP?
时间复杂度是指什么
图像复杂度对信息隐藏性能影响分析
商汤联合提出基于FPGA的Winograd算法:改善FPGA上的CNN性能 降低算法复杂度

如何求递归算法的时间复杂度
常见机器学习算法的计算复杂度
算法时空复杂度分析实用指南2
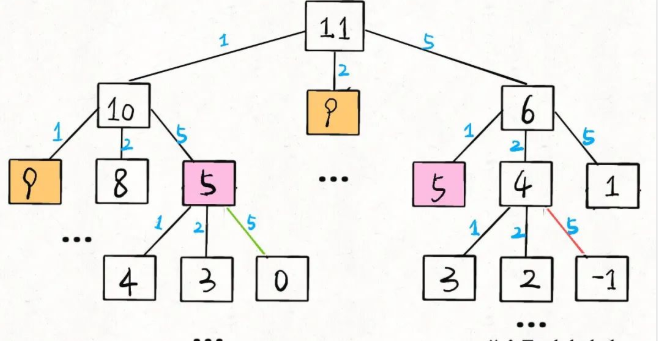




 算法时空复杂度分析实用指南(上)
算法时空复杂度分析实用指南(上)












评论