我们聊了聊LLC电路在调频模式下的一些特性,今天我们换个"环境"——聊聊LLC电路在移相控制下的特性。
首先我们先放一张LLC电路的基本拓扑:
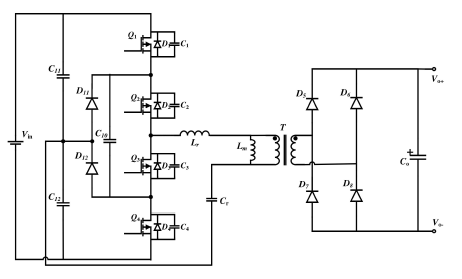
开关管Q1和Q4以及Q2和Q3互补导通180°,且Q2滞后Q1一定的角度。 定义移相比(两者的移相角与180°的比值)为D,有0≤D≤1。 变频开关频率恒定,并且满足fs=fr1,所以通过控制移相比D可以调节输出电压。 接下来我们主要分析其增益的特性,直观的来看,当移相角等于0时,输出电压的增益为1:移相角越大,输出电压越低,也就是电压增益越小。
下面给出了移相控制下谐振腔的输入电压波形:
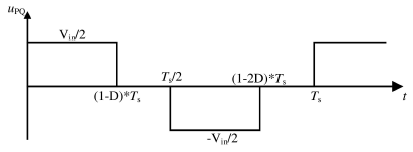
谐振腔的输入电压可以表示为:
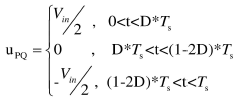
这里我们采用准确度较小的基波分析法仅定性地说明直流电压增益和移相比的关系。 将输入电压经过傅里叶变换得到基波电压如下:
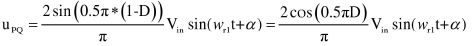
根据之前的输出电压基波分量我们可以得到,移相控制下的电压增益可以表示为:
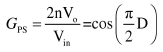
从上式可以知道,移相模式下的电压增益和移相比成近似余弦关系,并且变化范围为0~1。
为了保证电路在全范围运行下的高效率,我们需要对在移相控制下实现的ZVS的条件进行分析:
开关管Q1和Q4是超前管,其开通的谐振电流较大,故比较容易实现ZVS。 那滞后管Q2和Q3实现ZVS则较为艰难,下面我们主要分析它们实现ZVS的条件。
在前正半个周期内,励磁电感被输出电压钳位的时间是(1-D)Ts,则励磁电流的最大值为:
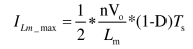
在前正半个周期内,励磁电感参与谐振的时间为DTs,这个阶段内谐振电流和励磁电流相等。 从Q3关断到Q2开始开通的死区时间内,Q2的寄生电容获得的电荷平衡关系可以知道:
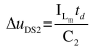
那么,实现ZVS的条件是:ΔuDS2≥Vin/2,则得到
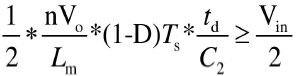
也就是下式得以成立:
上面式子的两边同时乘以电压的移相增益公式,可以得到下式
其中左边是关于移相角的减函数,邮编当死区时间确定时为一个常数,则左边存在一个最小值,当移相比大于该值时就不能实现Q2的ZVS。
我们不妨取
则可以得到相应的电压增益最小值,为:
关于LLC电路在移相控制下的,我们就聊聊以上这些,电压增益以及滞后管的ZVS实现条件。
-
调频
+关注
关注
8文章
233浏览量
55572 -
开关管
+关注
关注
4文章
226浏览量
21663 -
移相控制
+关注
关注
1文章
14浏览量
10654 -
LLC电路
+关注
关注
1文章
43浏览量
7533 -
电压增益
+关注
关注
1文章
28浏览量
4516
发布评论请先 登录
相关推荐
浅析基于碳化硅MOSFET的谐振LLC和移相电路在新能源汽车的应用
LLC谐振变换器的设计过程和LLC谐振变换器的移相控制特性分析
如何使用移相电路计算相位




 LLC电路在移相控制下的特性
LLC电路在移相控制下的特性












评论