哪怕只写过几行代码的人都会发现,编程基本上就是在跟数据打交道。计算机程序总是在接收数据、操作数据或返回数据。不管是求两数之和的小程序,还是管理公司的企业级软件,都运行在数据之上。
数据是一个广义的术语,可以指代各种类型的信息,包括最基本的数字和字符串。在经典的“Hello World!”这个简单程序中,字符串"Hello World!"就是一条数据。事实上,无论是多么复杂的数据,我们都可以将其拆成一堆数字和字符串来看待。
数据结构则是指数据的组织形式。看看以下代码。
x = "Hello!"y = "How are you"z = "today?"print x + y + z
这个非常简单的程序把3 条数据串成了一句连贯的话。如果要描述该程序中的数据结构,我们会说,这里有3 个独立的变量,分别引用着3 个独立的字符串。
在这里,你将学到,数据结构不只是用于组织数据,它还极大地影响着代码的运行速度。因为数据结构不同,程序的运行速度可能相差多个数量级。如果你写的程序要处理大量的数据,或者要让数千人同时使用,那么你采用何种数据结构,将决定它是能够运行,还是会因为不堪重负而崩溃。
一旦对各种数据结构有了深刻的理解,并明白它们对程序性能方面的影响,你就能写出快速而优雅的代码,从而使软件运行得快速且流畅。当然,你的编程技能也会更上一层楼。
接下来我们将会分析两种比较相似的数据结构:数组和集合。它们从表面上看好像差不多,但通过即将介绍的分析工具,你将会观察到它们在性能上的差异。
基础数据结构:数组
数组是计算机科学中最基本的数据结构之一。如果你用过数组,那么应该知道它就是一个含有数据的列表。它有多种用途,适用于各种场景,下面就举个简单的例子。
一个允许用户创建和使用购物清单的食杂店应用软件,其源代码可能会包含以下的片段。
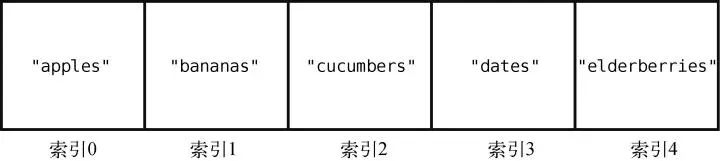
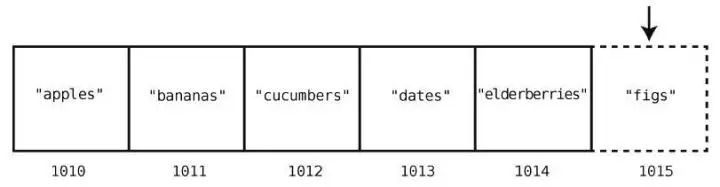
array = ["apples", "bananas", "cucumbers", "dates", "elderberries"]
这就是一个数组,它刚好包含5 个字符串,每个代表我会从超市买的食物。
此外,我们会用一些名为索引的数字来标识每项数据在数组中的位置。
在大多数的编程语言中,索引是从0 算起的,因此在这个例子中,"apples"的索引为0,"elderberries"的索引为4,如下所示。
若想了解某个数据结构(例如数组)的性能,得分析程序怎样操作这一数据结构。
一般数据结构都有以下4 种操作(或者说用法)。
- 读取:查看数据结构中某一位置上的数据。对于数组来说,这意味着查看某个索引所指的数据值。例如,查看索引2 上有什么食品,就是一种读取。
- 查找:从数据结构中找出某个数据值的所在。对于数组来说,这意味着检查其是否包含某个值,如果包含,那么还得给出其索引。例如,检查"dates"是否存在于食品清单之中,给出其对应的索引,就是一种查找。
- 插入:给数据结构增加一个数据值。对于数组来说,这意味着多加一个格子并填入一个值。例如,往购物清单中多加一项"figs",就是一种插入。
- 删除:从数据结构中移走一个数据值。对于数组来说,这意味着把数组中的某个数据项移走。例如,把购物清单中的"bananas"移走,就是一种删除。
接下来我们将会研究这些操作在数组上的运行速度。同时,我们也将学到第一个重要理论:操作的速度,并不按时间计算,而是按步数计算。
为什么呢?
因为,你不可能很绝对地说,某项操作要花5 秒。它在某台机器上要跑5 秒,但换到一台旧一点的机器,可能就要多于5 秒,而换到一台未来的超级计算机,运行时间又将显著缩短。所以,受硬件影响的计时方法,非常不可靠。
然而,若按步数来算,则确切得多。如果A 操作要5 步,B 操作要500 步,那么我们可以很肯定地说,无论是在什么样的硬件上对比,A 都快过B。因此,衡量步数是分析速度的关键。
此外,操作的速度,也常被称为时间复杂度。本文中,我们提到速度、时间复杂度、效率、性能,它们其实指的都是步数。
事不宜迟,我们现在就来探索上述4 种操作方式在数组上要花多少步。
- 读取
首先看看读取,即查看数组中某个索引所指的数据值。
这只要一步就够了,因为计算机本身就有跳到任一索引位置的能力。在["apples","bananas", "cucumbers", "dates", "elderberries"]的例子中,如果要查看索引2 的值,那么计算机就会直接跳到索引2,并告诉你那里有"cucumbers"。
计算机为什么能一步到位呢?原因如下。
计算机的内存可以被看成一堆格子。下图是一片网格,其中有些格子有数据,有些则是空白。

当程序声明一个数组时,它会先划分出一些连续的空格子以备使用。换句话说,如果你想创建一个包含5 个元素的数组,计算机就会找出5 个排成一行的空格子,将其当成数组。

内存中的每个格子都有各自的地址,就像街道地址,例如大街123 号。不过内存地址就只用一个普通的数字来表示。而且,每个格子的内存地址都比前一个大1,如下图所示。

购物清单数组的索引和内存地址,如下图所示。

计算机之所以在读取数组中某个索引所指的值时,能直接跳到那个位置上,是因为它具备以下条件。
(1) 计算机可以一步就跳到任意一个内存地址上。(就好比,要是你知道大街123 号在哪儿,那么就可以直奔过去。)
(2) 数组本身会记有第一个格子的内存地址,因此,计算机知道这个数组的开头在哪里。
(3) 数组的索引从0 算起。
回到刚才的例子,当我们叫计算机读取索引3 的值时,它会做以下演算。
(1) 该数组的索引从0 算起,其开头的内存地址为1010。
(2) 索引3 在索引0 后的第3 个格子上。
(3) 于是索引3 的内存地址为1013,因为1010 + 3 = 1013。
当计算机一步跳到1013 时,我们就能获取到"dates"这个值了。
所以,数组的读取是一种非常高效的操作,因为它只要一步就好。一步自然也是最快的速度。这种一步读取任意索引的能力,也是数组好用的原因之一。
如果我们问的不是“索引3 有什么值”,而是“"dates"在不在数组里”,那么这就需要进行查找操作了。下面我们就来看看。
2.查找
如前所述,对于数组来说,查找就是检查它是否包含某个值,如果包含,还得给出其索引。
那么,我们就试试在数组中查找"dates"要用多少步。
对于我们人来说,可以一眼就看到这个购物清单上的"dates",并数出它的索引为3。但是,计算机并没有眼睛,它只能一步一步地检查整个数组。
想要查找数组中是否存在某个值,计算机会先从索引0 开始,检查其值,如果不匹配,则继续下一个索引,以此类推,直至找到为止。
我们用以下图来演示计算机如何从购物清单中查找"dates"。
首先,计算机检查索引0。

因为索引0 的值是"apples",并非我们所要的"dates",所以计算机跳到下一个索引上。

索引1 也不是"dates",于是计算机再跳到索引2。

但索引2 的值仍不匹配,计算机只好再跳到下一格。

啊,真是千辛万苦,我们找到"dates"了,它就在索引3 那里。自此,计算机不用再往后跳了,因为结果已经得到。
在这个例子中,因为我们检查了4 个格子才找到想要的值,所以这次操作总计是4 步。
这种逐个格子去检查的做法,就是最基本的查找方法——线性查找。当然还可以学习其他查找方法,但在那之前,我们再思考一下,在数组上进行线性查找最多要多少步呢?
如果我们要找的值刚好在数组的最后一个格子里(如本例的elderberries),那么计算机从头到尾检查每个格子,会在最后才找到。同样,如果我们要找的值并不存在于数组中,那么计算机也还是得查遍每个格子,才能确定这个值不在数组中。
于是,一个5 格的数组,其线性查找的步数最大值是5,而对于一个500 格的数组,则是500。
以此类推,一个N 格的数组,其线性查找的最多步数是N(N 可以是任何自然数)。
可见,无论是多长的数组,查找都比读取要慢,因为读取永远都只需要一步,而查找却可能需要多步。
接下来,我们再研究一下插入,准确地说,是插入一个新值到数组之中。
-
数据
+关注
关注
8文章
7077浏览量
89161 -
计算机
+关注
关注
19文章
7513浏览量
88173 -
代码
+关注
关注
30文章
4798浏览量
68725 -
数据结构
+关注
关注
3文章
573浏览量
40152
发布评论请先 登录
相关推荐
数据结构的几个重要知识点
什么是数据结构
数据结构在游戏编写中的应用
数据结构是什么_数据结构有什么用
为什么要学习数据结构?数据结构的应用详细资料概述免费下载
什么是数据结构?为什么要学习数据结构?数据结构的应用实例分析
大牛分享平时如何学习数据结构与算法
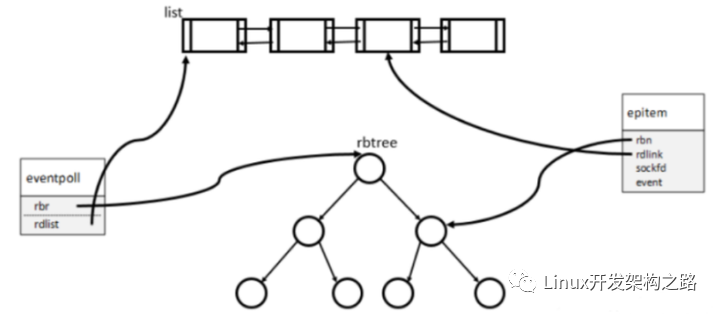
epoll的基础数据结构




 为什么说数据结构很重要1
为什么说数据结构很重要1










评论