海森堡不确定性原理是德国物理学家维尔纳·海森堡于1927年提出的,它表明在量子力学里,粒子的位置和动量不可能同时被精确地测量,位置的不确定性和动量的不确定性的乘积必然大于等于普朗克常数除以4π(公式:ΔxΔp≥h/4π)。这意味着,微观世界的粒子行为与我们熟悉的宏观物质很不一样,它们具有一种随机性和概率性,而不是绝对的确定性和因果性。
那么,海森堡不确定性原理的本质是什么呢?为什么我们不能同时知道一个粒子的位置和动量呢?这与我们的生活有什么关系呢?要回答这些问题,我们需要从两个方面来理解海森堡不确定性原理:一是测量的角度,二是波函数的角度。
从测量的角度来看,海森堡不确定性原理反映了对于微观粒子的测量所面临的固有限制。要测量一个粒子的位置或动量,我们需要用另一个粒子或波来与之相互作用,比如用光子或电子来照射它。但是,这样做就会不可避免地扰动被测量粒子的运动状态,从而改变它的位置或动量。
而且,扰动的程度与我们用来测量的粒子或波的能量或波长有关。如果我们想要更精确地测量位置,就需要用更短波长或更高能量的粒子或波来照射它,这样就会造成更大的扰动,从而使得动量更不确定;反之亦然。因此,位置和动量之间存在着一个无法突破的平衡点。
从波函数的角度来看,海森堡不确定性原理反映了微观粒子具有波粒二象性的本质特征。在量子力学中,微观粒子可以用波函数来描述,波函数是一个复数函数,它在位置空间或动量空间中给出了粒子出现在某处或具有某种动量的概率密度。因此,波函数又叫做概率幅。根据波恩的概率解释,波函数在位置空间中的模方表示了粒子在空间中分布的概率密度;而波函数在动量空间中的模方表示了粒子具有不同动量值的概率密度。
而位置空间中的波函数和动量空间中的波函数之间存在着一个傅里叶变换的关系。这个关系可以用一个定理来表述,即傅里叶变换的不确定性原理,也称为时间-频率不确定性原理。这个原理说的是,一个信号不可能同时在频域和时域具有任意小的分辨率,如果它在时间域上变得越窄,那么它在频率域上就会变得越宽,反之亦然。
那么,这个傅里叶变换的不确定性原理和海森堡不确定性原理有什么关系呢?事实上它们是等价的,如果我们把傅里叶变换的不确定性原理应用到位置和动量上,就可以得到海森堡不确定性原理。也就是说,海森堡不确定性原理是傅里叶变换的不确定性原理在量子力学中的应用。 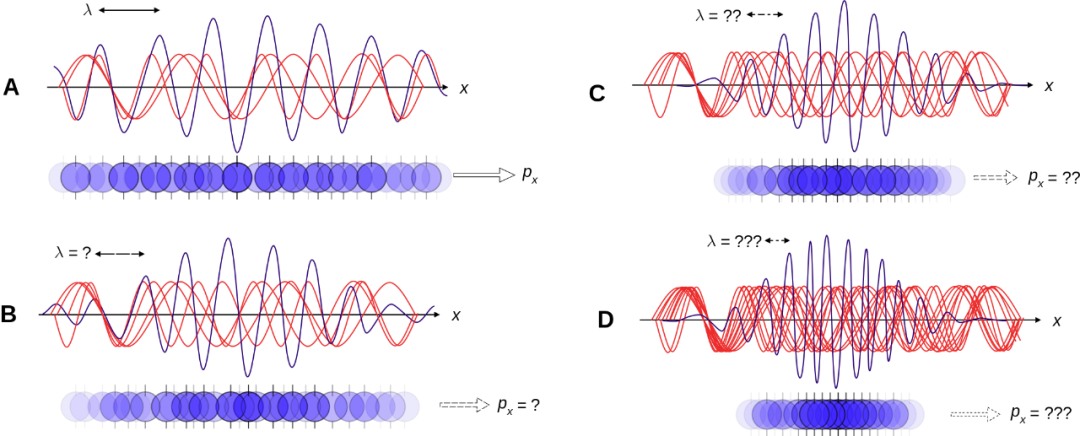
那么,海森堡不确定性原理与我们的生活有什么关系呢?其实,在我们日常经验的尺度上,海森堡不确定性原理是可以忽略的。因为普朗克常数非常小(约为6.626×10^-34 J·s),所以位置和动量的不确定性也非常小。这意味着,在宏观世界中,我们可以同时知道一个物体的位置和动量,并且可以用牛顿力学来描述它们之间的因果关系。
但是,在微观世界中,海森堡不确定性原理就不能忽略了。因为微观粒子的质量和速度都非常小,所以位置和动量的不确定性就相对较大。这意味着,在微观世界中,我们不能同时知道一个粒子的位置和动量,并且不能用牛顿力学来描述它们之间的因果关系。而这就给我们对微观现象的认识带来了机遇与挑战。
例如,微观世界的不确定性导致了隧道效应,即一个粒子可以以一定的概率穿越一个本来无法越过的势垒。这个效应在核物理、半导体、超导等领域有重要的应用。微观世界的不确定性导致了量子涨落,即真空中会不断地产生和湮灭一对正负虚粒子。这个效应在宇宙学、黑洞物理、粒子物理等领域有重要的应用。
审核编辑:刘清
-
傅里叶变换
+关注
关注
6文章
439浏览量
42583 -
小波函数
+关注
关注
0文章
2浏览量
4842
原文标题:从测量和波函数角度理解海森堡不确定性原理
文章出处:【微信号:bdtdsj,微信公众号:中科院半导体所】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
计及多重不确定性的规模化电动汽车接入配电网调度方法及解决方案
英特尔德国晶圆厂命运未卜,政府紧急预案防撤资
英特尔德国晶圆厂项目不确定性加剧,地方政府忧虑投资或将撤销
相对于人工的不确定性,机器人码垛有何优势
ETAS推出Time-Triggered Scheduling (TTS)的确定性调度解决方案
海能达起诉美国法院产品禁售令被暂停
什么是嵌入式实时系统的确定性?简析EDMS中的确定性
海信马晓龙:坚定长期主义的战略定力,激发“确定性”增长的内生动力

上海交大科研团队使用Moku:pro推进在量子光学实验中的多参数估计

确定性网络威廉希尔官方网站 如何提高网络的可靠性?

智能制造的本质是解决不确定性




 海森堡不确定性原理的本质是什么呢?
海森堡不确定性原理的本质是什么呢?












评论