
继续讲解!上堂课讲到FIR滤波器的线性相位特点,分析了线性相位带来的延时特性。本堂课继续讲解FIR滤波器的幅度特性,再理论联系实际的看看FIR滤波器到底长什么样?有什么用?听我慢慢道来。




在MATLAB自带的函数中,有fir1和fir2函数。前者是是用窗函数法设计线性相位FIR的工具箱函数,以实现线性相位FIR的标准窗函数法设计。后者是基于频率基本法的FIR滤波器设计,用于任意频率响应的加窗数字FIR滤波器的设计。
信号通常是一维数组,可以用fir1和fir2函数处理。二维数组处理方式会有些差异。图像处理中会涉及二维数组的处理,这里只是提一下,能让同学们有个了解。二维数据主要是图像数据,图像滤波主要用imfilter函数。可以用fspecial函数预定义各种二维滤波器。这些知识会在《数字图像处理》课程中详细讲解,这里不再赘述。

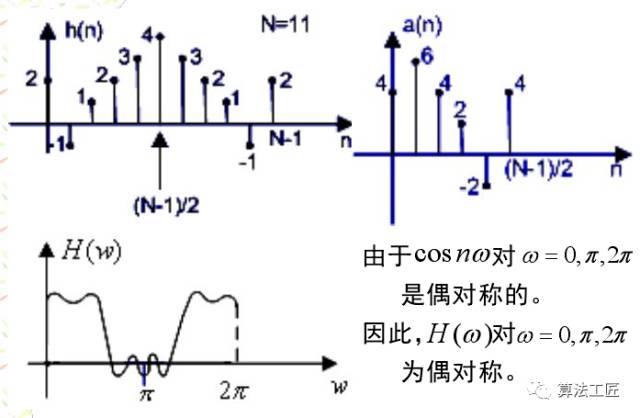



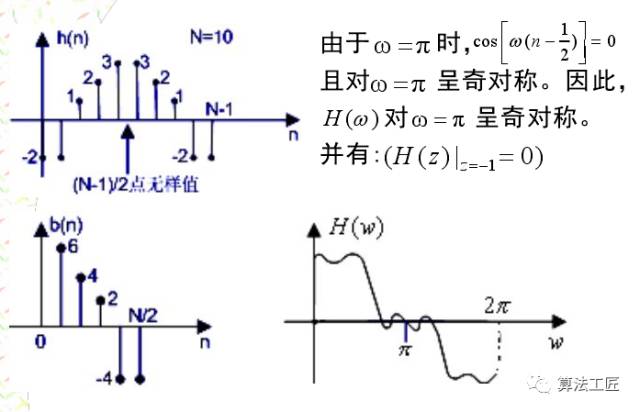



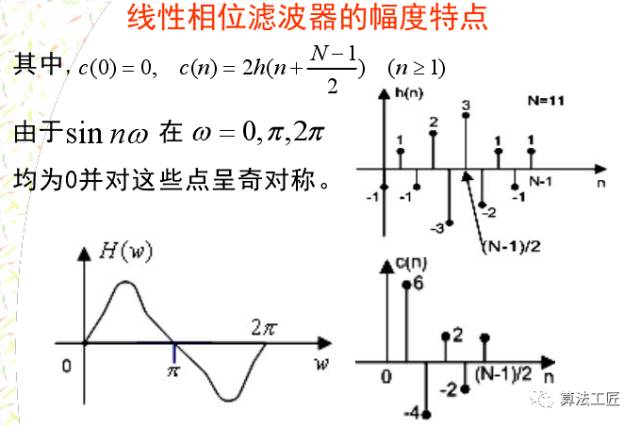



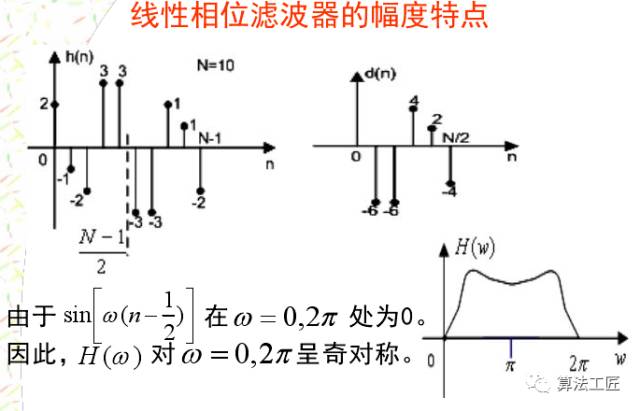





讲完这些理论,来一些涉及程序仿真的内容,看看理论能不能联系实际!
公众号的这部分内容会让你理论联系仿真!

信号中经常混有各种复杂成分,有需要的成分,也有不需要的成分。很多信号分析都是基于滤波器而进行, 因此数字滤波器占有极其重要的地位 。数字滤波器是具有一定传输选择特性的数字信号处理装置,其输入与输出均为数字信号实质上是一个由有限精度算法实现的线性时不变离散系统。它的基本工作原理是利用离散系统特性对系统输入信号进行加工和变换,改变输入序列的频谱或信号波形,让有用频率的信号分量通过,抑制无用的信号分量输出。数字滤波器和interwetten与威廉的赔率体系 滤波器有着相同的滤波概念,根据其频率响应特性可分为低通、高通、带通、带阻等类型。与模拟滤波器相比,数字滤波器除了具有数字信号处理固有优点外,还有精度高、稳定性好、灵活性强等优点。FIR滤波器具有线性相位,但它的传递函数的极点固定在原点,只能通过改变零点位置来改变性能,为了达到高的选择性必须用较高的阶数。对于同样的滤波器设计指标,FIR滤波器要求的阶数可能比IIR滤波器高10倍以上。
由于FIR数字滤波器具有严格的相位特性,对于信号处理和数据传输是很重要的。目前 FIR滤波器的设计方法主要有三种:窗函数法、频率抽样法和优化设计(切比雪夫逼近)方法。我们重点学习窗函数法。上堂课也简单提及了一下!










看看结果吧!
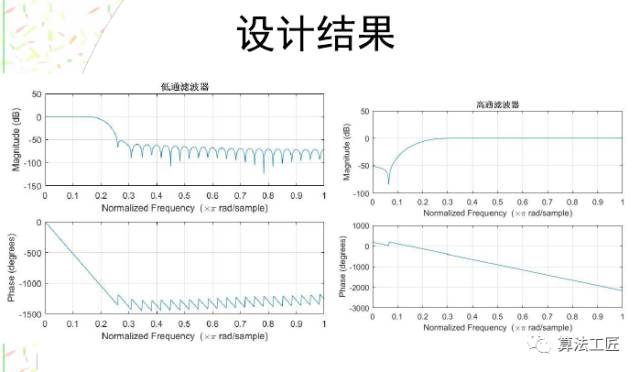

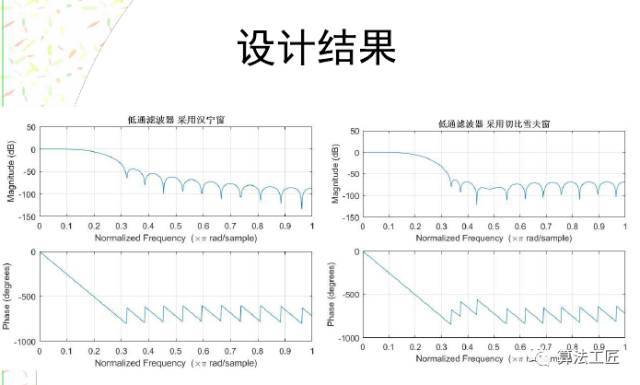




学以致用!而且必须致用!
不然何为工科生?
作业来了,因为偏向应用,所以编程的内容较多,等待大家的程序运行结果。

在第一版文章中,对fir2函数的描述有错误。这个函数不是用来处理二维数组的!它可以用于设计有任意频率响应的加窗FIR滤波器。对标准的低通、带通、高通和带阻滤波器的设计可使用fir1函数。
语法:b = fir2(n,f,m)
设计出一个n阶的FIR滤波器。其滤波器的频率特性由参数f和m决定。参数f为频率点矢量,且f∈[0,1],f=1对应于0.5fs。矢量f按升序排列,且第一个元素必须是0,最后一个必须为1,并可以包含重复的频率点。矢量m中包含了与f相对应的期望得到的滤波器的幅度。f为归一化频率向量。举例如下:设计一个100阶的低通滤波器。运行一下下图中的代码,看看能出什么结果?
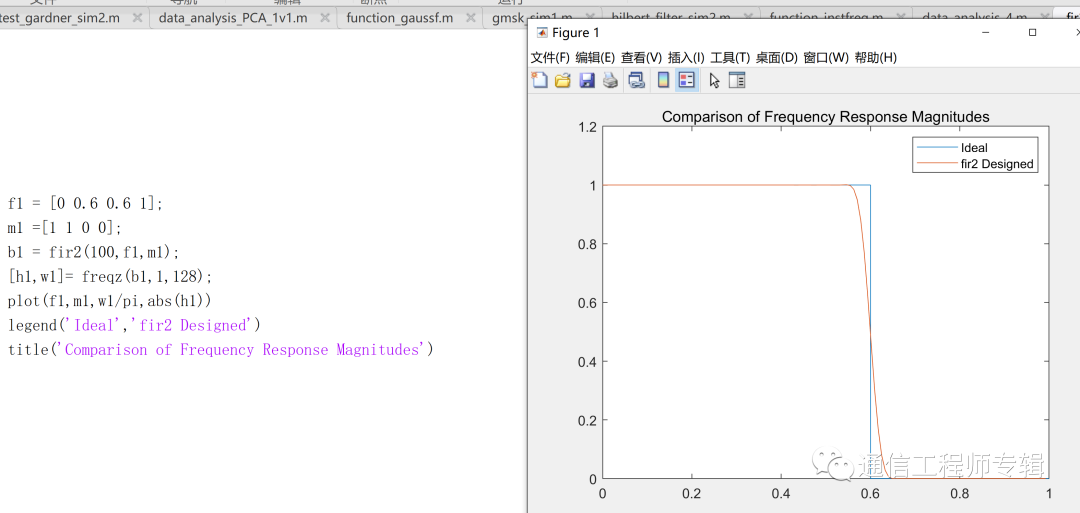

如果要求设计一个奇怪形状的滤波器呢?
比如设计一个80阶的FIR滤波器,要求滤波器0到π/4的幅度响应为0 ,π/4到π/2的幅度响应为1/4,π/2到3π/4的幅度响应为0,3π/4到1的幅度响应为1。采用切比雪夫窗。该怎么写程序呢?
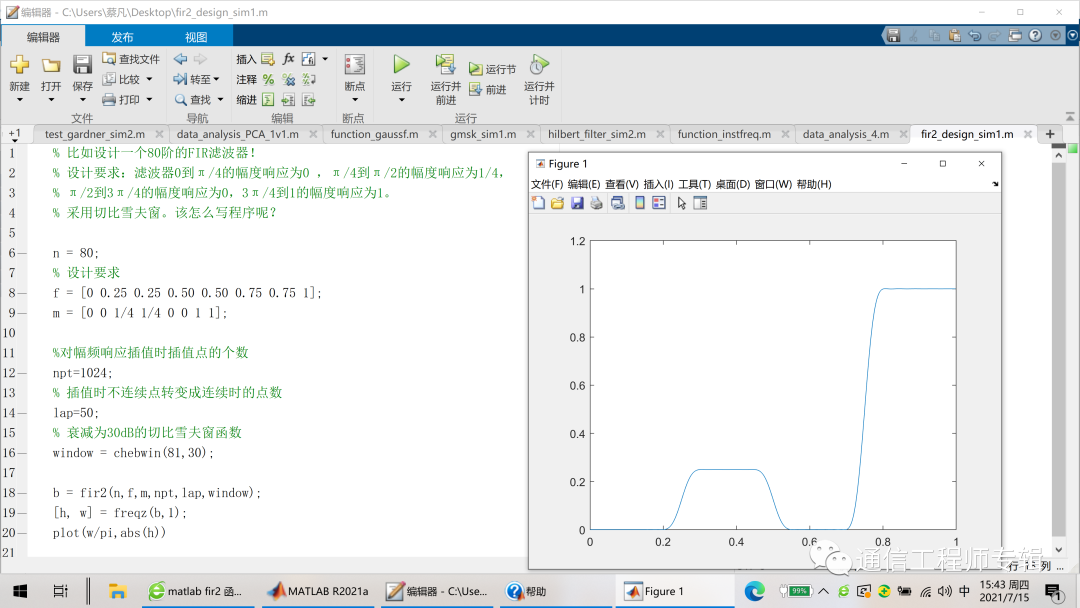
有程序有图就有真正的理解!
再回到二维数组的话题!之前学过的卷积和滤波函数都是针对一维数组使用,那么能针对二维数组吗?在MATLAB中,filter2 函数实现二维数字滤波器。conv2 函数实现二维卷积。之前本人搞混淆了,记成了fir2是用来实现二维数字滤波器的函数,在此更正一下!
现在Python非常流行,很多人也会使用Python来完成信号处理的仿真。提示一下。在 Python中,MATLAB filter2的等效函数是 scipy.signal.correlate2d。MATLAB conv2的等效函数是 scipy.signal.convolve2d。要先安装scipy库文件,才能调用这两个函数。数字信号处理理论的发展过程很缓慢,因为之前的科学家已经研究的很透彻了,但软件的发展一直在加速。应用什么样的软件来进行数字信号处理的仿真可以根据自己的喜好来选择。我个人推荐MATLAB,相关仿真的文章在本公众号里面可以找到!但是针对数据分析呢?我推荐Python。在语言类分析的场合,它更是功效无穷!本章完结!

20170531记录:
原文标题:数字信号处理v2 第七章 FIR数字滤波器的设计方法(2)
-
通信网络
+关注
关注
21文章
2041浏览量
52061
发布评论请先 登录
相关推荐
AMC1304后接的数字滤波器接口应该是什么样的?
ADC3663数字滤波器如何使用呢?
基于FPGA实现FIR数字滤波器
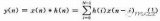
数字滤波器的原理和应用




 数字信号处理v2 第七章 FIR数字滤波器的设计方法(2)
数字信号处理v2 第七章 FIR数字滤波器的设计方法(2)












评论