正弦稳态电路的分析

1、向量法基础

（3）复数的运算法则

根据上述公式可知，复数的加减运算采用代数形式较为方便，而复数的乘除法则采用极坐标形式比较方便。

（5）正弦信号的一种重要性质：正弦量乘以一个常数，正弦量的微分，积分，同频率正弦量的代数和，其结果均为一个同频率的正弦量。工程中默认一个正弦信号的有效值和最大值之间的关系为：最大值是有效值的根号2倍。正弦量的有效值与正弦量的频率，初相位无关。

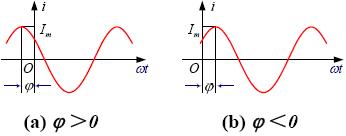
（6）电路中通常采用“超前”和 “滞后”等概念来说明两个同频率正弦量相位的比较结果。注意：只有两个同频率的正弦量才可以比较相位。

2、阻抗和导纳

（1）根据电阻的性质可知，流过电阻R的电流和电阻R两端的电压同相位，故电阻的向量形式为R。

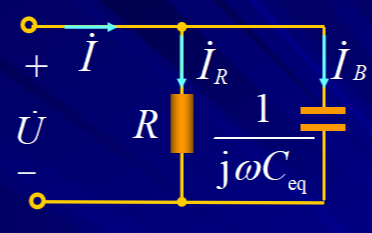
（4）正弦交流电路中，整个电路的阻抗可以利用直流电路的电阻等效原理，即容抗和感抗均可以看做一个电阻，通过电阻的串并联就可以解得电路的阻抗。导纳则是阻抗的倒数。

（5）由于正弦电路采用了向量法表示元件参数，故直流电路中的电阻等效，电源等效，叠加定理，戴维南等效（诺顿等效），回路电流，网孔电流，节点电压等定理对于交流电路均成立。

3、向量图分析

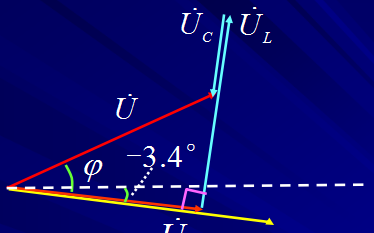
向量图分析可以作为当不知道电路的具体参数，仅知道有效值时候的电路分析使用，假定一个电压或电流作为参考量，计算出对于这个参考电压的相位，通过向量的和或差的形式求解出需要的电流或电压的有效值的一种方法。在交流电路分析中是一种很简便直观的方法。

6、例题分析

例题1：将下列复数化为极坐标形式

例题2：将下列复数化为代数形式