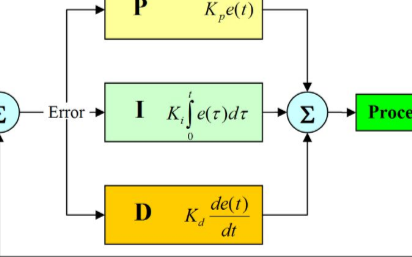
2.1 PID算法数学推导过程
2.1.1 连续系统的PID算法

2.1.2 PID算法的离散化

2.2 位置型PID算法
2.2.1 MATLAB算法
clc
clear
%PID初始化
len = 500 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.2; %比例系数
Kd = 0.2; %微分值
Ki = 0.015 ; %积分值
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
integral = integral+err_last; %误差累计
y_d_last = Kp* err_0 + Ki*integral + Kd*( err_1- err_0); %位置型PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
MATLAB运行结果如下图所示。

2.2.2 C算法
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.015 ;
}
float PID_Realize( float Speed )
{
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
pid.integral += pid.err ;
pid.voltage = pid.Kp*pid.err+pid.Ki*pid.integral+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<850 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
}
}
2.3 增量型PID算法
2.3.1 MATLAB算法
clc
clear
%PID初始化
len = 400 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
err_2 = 0 ; %k-2时刻误差
y_d_last = 0 ; %k-1时刻输出
increment = 0 ; %增量
Kp = 0.2; %比例系数
Kd = 0.2; %微分值
Ki = 0.015 ; %积分值
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
increment = Kp*(err_0-err_1) + Ki*err_0 + Kd*(err_0-2*err_1+err_2);%增量型PID运算公式
err_2 = err_1;
err_1 = err_0;
y_d_last = y_d_last + increment ; %输出叠加
%更新参数
y_d(k) = y_d_last ;
err(k) = err_2;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
MATLAB运行结果如下图所示。

2.3.2 C算法
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_next ; //上一次误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.err_next = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.015 ;
}
float PID_Realize( float Speed )
{
float incrementSpeed ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
incrementSpeed=
pid.Kp*(pid.err-pid.err_next)+pid.Ki*pid.err+pid.Kd*( pid.err-2*pid.err_next+pid.err_last ) ;
pid.err_last = pid.err_next ;
pid.err_next = pid.err ;
pid.ActualSpeed += incrementSpeed ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<850 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
}
}
2.4 积分分离型PID算法
2.4.1 实现原理
为了消除系统的稳态误差,提高控制精度引入了积分环节,但是在启动,结束和大幅度增减设定时,短时间内系统输出有很大的偏差,会造成PID运算的积分积累,导致控制量超过执行机构可能允许的最大动作范囲所对应的极限控制量,从而引起较大的超调,甚至震荡,为了克服这一问题,引入了积分分离的概念,基本思路是“当给定值与反馈值偏差较大时,取消积分的作用,当被控量接近给定值时,引入积分控制”,用于消除稳态误差,提高系统的精度。
2.4.2 MATLAB算法
clc
clear
%PID初始化
len = 500 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.2; %比例系数
Kd = 0.2; %微分值
Ki = 0.015 ; %积分值
max = 400 ; %积分上限
index = 0 ; %积分有效性
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %误差累计
else
index = 0 ;
end
y_d_last = Kp*err_0 + Ki*index*integral + Kd*(err_1-err_0); %位置型PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
MATLAB运行结果如下图所示。

2.4.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
float umax ; //积分上限
float umin ; //积分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( abs(pid.err)<= pid.umax )
{
index = 1 ;
pid.integral += pid.err ;
}
else
index = 0 ;
pid.voltage = pid.Kp*pid.err+index*pid.Ki*pid.integral+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<1000 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
printf( "%.2f\\n" , Speed ) ;
}
}
2.5 抗积分饱和型PID算法
2.5.1 实现原理
所谓积分饱和现象是指如果系统存在一个方向的偏差,PID控制器的输出会因为存在积分环节而不断累积增大,从而导致执行机构达到极限位置,若控制器输出响应继续增大,执行器开度不可能再增大,此时计算机输出控制量超出了正常运行范围而进入饱和区,一旦系统出现反向偏差,输出响应逐渐从饱和区退出,进入饱和区时间越长则退出饱和区的时间也就随之增加,这段时间里,执行机构仍然停留在极限位置而不能随着偏差方向立即作出相应的改变,造成控制性能恶化,这种现象称为积分饱和现象或积分失控现象。实现抗积分饱和算法的基本思路是计算系统的响应时,首先判断上一时刻的控制量是否超出了极限范围,如果超过上限,则只累计反向偏差,若低于下限,则只累计正向偏差,从而避免控制量长时间停留在饱和区。
2.5.2 MATLAB算法
clc
clear
%PID初始化
len = 180 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.2; %比例系数
Kd = 0.2; %微分值
Ki = 0.1 ; %积分值
max = 400 ; %积分上限
min = -200 ; %积分下限
index = 0 ; %积分有效性
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %误差累计
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral + Kd*(err_1-err_0); %位置型PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
MATLAB运行结果如下图所示。

2.5.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
float umax ; //积分上限
float umin ; //积分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
2.6 梯形积分PID算法
2.6.1 实现原理
根据梯形算法的积分环节公式

作为PID控制的积分项,其作用是消除余差,为了尽量减小余差,应提高积分项运算精度,为此可以将矩形积分改为梯形积分,具体实现的语句为pid.voltage = pid.Kppid.err+indexpid.Ki pid.integral/2+pid.Kd ( pid.err-pid.err_last ) ;
2.6.2 MATLAB算法
clc
clear
%PID初始化
len = 358 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.2; %比例系数
Kd = 0.2; %微分值
Ki = 0.1 ; %积分值
max = 400 ; %积分上限
min = -200 ; %积分下限
index = 0 ; %积分有效性
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
if y_d_last>max
if abs(err_0) <= y(k)
index = 1 ;
if err_0 < 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
elseif y_d_last<min
if abs(err_0) <= y(k)
index = 1 ;
if err_0 > 0
integral = integral+err_0; %误差累计
end
else
index = 0 ;
end
else
if abs(err_0) <= y(k)
index = 1 ;
integral = integral+err_0; %误差累计
else
index = 0 ;
end
end
y_d_last = Kp*err_0 + Ki*index*integral/2 + Kd*(err_1-err_0); %PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
MATLAB运行结果如下图所示。

2.6.3 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
float umax ; //积分上限
float umin ; //积分下限
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.2 ;
pid.Kd = 0.2 ;
pid.Ki = 0.1 ;
pid.umax = 400 ;
pid.umin = -200 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( pid.ActualSpeed>pid.umax )
{
if( abs(pid.err)<=200 )
{
index = 1 ;
if( pid.err<0 )
pid.integral += pid.err ;
}
else
index = 0 ;
}
else if( pid.ActualSpeed
2.7 变积分PID算法
2.7.1 实现原理
变积分PID可以看做是积分分离的PID算法的更一般形式,在普通的PID控制算法中,由于积分系数是常数,所以在整个控制过程中,积分增量是不变的,但是,系统对于积分项的要求是,系统偏差较大时,积分作用应该减弱甚至全无,而在偏差较小时,则应该加强,积分系数取大了会引起超调,甚至积分饱和,取小了又不能短时间内消除静差,因此,需要根据系统偏差的大小改变积分速度。
变积分PID的基本思想是改变积分项的累加速度,使其与偏差大小相对应,偏差越大,积分越慢,偏差较小,积分越快。
这里给积分系数前加一个比例系数index,使最终的比例环节的积分系数为Ki*index。
2.7.1 MATLAB算法
clc
clear
%PID初始化
len = 200 ; %运算次数
y = zeros(1,len); %期望值
y_d = zeros(1,len); %过程值
err = zeros(1,len); %误差值
err_0 = 0 ; %k时刻误差
err_1 = 0 ; %k-1时刻误差
y_d_last = 0 ; %k-1时刻输出
integral = 0; %积分值
Kp = 0.4; %比例系数
Kd = 0.2; %微分值
Ki = 0.2 ; %积分值
max = 400 ; %积分上限
min = -200 ; %积分下限
index = 0 ; %积分有效性
%运算过程
for k=1:1:len
y(k) = 200 ; %期望输出
err_0 = y(k)-y_d_last; %计算偏差
if abs(err_0) > max
index = 0 ;
elseif abs(err_0) < min
index = 1 ;
integral = integral+err_0; %误差累计
else
index = ( max-abs(err_0) )/20 ;
integral = integral+err_0; %误差累计
end
y_d_last = Kp*err_0 + Ki*index*integral/2 + Kd*(err_1-err_0); %PID运算公式
err_1 = err_0 ;
%更新参数
y_d(k) = y_d_last ;
err(k) = err_1 ;
end
%输出图像绘制
t = 1:1:len;
subplot( 2, 1, 1 ) ;
plot( t, y, 'r', t, y_d, 'b' );
axis([0 len, 0 1.5*y(1)])
title('输出曲线');
xlabel('t')
ylabel('y(t)')
%误差图像绘制
subplot( 2, 1, 2 ) ;
plot( t, err );
axis([0 len, 0 1.5*y(1)])
title('误差曲线');
xlabel('t')
ylabel('e(t)')
MATLAB运行结果如下图所示。

2.7.2 C算法
#include
#include
struct _pid
{
float SetSpeed ; //设置速度
float ActualSpeed ; //实际速度
float err ; //误差
float err_last ; //最终误差
float Kp , Kd , Ki ; //比例系数
float voltage ; //输出电压
float integral ; //积分值
}pid;
void PID_Init()
{
pid.SetSpeed = 0 ;
pid.ActualSpeed = 0.0 ;
pid.err = 0.0 ;
pid.err_last = 0.0 ;
pid.voltage = 0.0 ;
pid.integral = 0.0 ;
pid.Kp = 0.4 ;
pid.Kd = 0.2 ;
pid.Ki = 0.2 ;
}
float PID_Realize( float Speed )
{
char index ;
pid.SetSpeed = Speed ;
pid.err = pid.SetSpeed-pid.ActualSpeed ;
if( abs(pid.err)>200 )
index = 0 ;
else if( abs(pid.err)<180 )
{
index = 1 ;
pid.integral += pid.err ;
}
else
{
index = ( 200-abs(pid.err) )/20 ;
pid.integral += pid.err ;
}
pid.voltage = pid.Kp*pid.err+index*pid.Ki*pid.integral/2+pid.Kd*( pid.err-pid.err_last ) ;
pid.err_last = pid.err ;
pid.ActualSpeed = pid.voltage*1.0 ;
return pid.ActualSpeed ;
}
void main()
{
int count ;
count = 0 ;
PID_Init() ;
while( count<150 )
{
float Speed = PID_Realize( 200.0 ) ;
count ++ ;
printf( "%.2f\\n" , Speed ) ;
}
}
2.8 专家PID与模糊PID算法思想
PID的控制思想非常简单,主要就是比例,积分和微分环节的参数整定过程,对于执行期控制模型确定或者控制模型简单的系统来说,参数的整定可以通过计算获得,对于一般精度要求不是很高的执行器系统,可以采用拼凑的方法进行实验型的整定。
但是,实际的系统大部分属于非线性系统,或者说是系统模型不确定的系统,如果控制精度要求较高的话,那么对于参数的整定过程也是有难度的,专家PID和模糊PID就是为了满足这方面的需求而设计的,专家算法和模糊算法都归属于智能算法的范畴,智能算法最大的优点就是在控制模型未知的情况下,可以对模型进行控制,这里需要注意的是,专家PID也好,模糊PID也好,绝对不是专家系统或模糊算大与PID控制算法的简单加和,它是专家系统或者模糊算法在PID控制器参数整定上的应用,也就是说,智能算法是辅助PID进行参数整定的手段。
关于专家PID的C语言实现,需要找到一些依据,还需要从PID系数本身考虑。
1、比例系数Kp的作用是加快系统的响应速度,提高系统的调节精度,Kp越大,系统的响应速度越快,调节的精度越高,但是容易产生超调,甚至会引起系统不稳定,Kp取值过小,则会降低系统的调节精度,拖慢响应速度,从而延长调节时间,使系统的静态,动态特性变差。
2、积分系数Ki的作用是消除系统的稳态误差,Ki越大,系统的静态误差消除得越快,但是若Ki过大,在响应过程的初期就会产生积分饱和的现象,从而引起相应过程的较大超调,若Ki过小,将使系统静态误差难以消除,影像系统的调节精度。
3、微分系数Kd的作用是改善系统的动态特性,其作用主要是在响应过程中抑制偏差向任何方向的变化,对偏差变化进行提前预报,但是若Kd过大,会使响应过程提前制动,从而延长调节时间,而且会降低系统的抗干扰性。

2.9 PID算法应用——电机转速控制
PID是一种广泛应用在控制理论中的算法,以直流电机为例,要想精确控制电机的转速就需要形成一种闭环控制思想。首先将一个默认的输入端的电压值发送给直流电机,通过转速传感器将当前电机的转速反馈到输入端,通过与输入端做运算,如果转速高于设定的值,则减小输入端电压,如果转速低于设定的值,则提高输入端电压,由此形成了一种闭环控制回路,即通过不停的对输出端进行反馈,以达到精确控制的目的。为了使控制系统的速度更快,精确性更高,稳定性更强,PID控制器被广泛应用在了这里面,现在我们通过MATLAB的Simulink来实现直流电机的PID控制。

一个直流电机的模型如上图所示,为了简化讨论,假设转子和转轴都是刚体,且转子受到的磁场恒定,转子收到的摩擦力与速度成正比,该电机的物理参数为:
(1)转子的转动惯量J=0.01kg·m^2^
(2)电机摩擦系数b=0.01N···m·s
(3)电动势常数Ke=0.01V/rad/sec
(4)电机扭矩常数Kt=0.01N·m/Amp
(5)电阻R=1Ω
(6)电感L=0.5H

我们希望控制器输入1V电压的时候稳定状态下保持0.1rad/sec的转速,稳定时间2s,稳态误差低于1%,受到阶跃输入干扰的时候超调小于5%。Matlab的仿真并不像之前学习51的时候用的Protuse一样,可以看到直观效果,Matlab的仿真实际是对数学的计算过程,即输入与输出必须都抽象成函数表达式进行,通过观察输出的函数表达式与波形来判断系统的工作状态与性能。我们将上面得到的复频域下的函数表达式代入参数,得到

通过Simulink创建仿真图如下图所示。

双击PID控制器的图标,打开了以下对话框。

对话框内的这三个参数就是PID控制器的三个参数,其中Proportional代表比例环节,Integral代表积分环节,Derivative代表微分环节,通过修改这三个参数达到实现控制系统的目的。
在PID控制中,这三个参数分别对系统控制有以下几个作用:
(1)比例环节P:控制输出响应的速度,减小稳态误差,但是会增大超调量
(2)积分环节I:消除系统的稳态误差,加快达到稳定所需的时间,但也会增大超调量
(3)微分环节D:加快动态过程,容易引起系统震荡,同样,微分环节也会增大超调量
为了满足:
(1)稳定时间2s
(2)稳态误差低于1%
(3)超调小于5%
这三个条件,我们首先修改比例环节,用来满足稳态误差低于1%这个参数。通过实验发现,当比例环节设定在100以上的时候,稳态误差低于1%,如下图所示。

但是我们发现

即系统的超调量较大,达到了20%,此时需要调节微分环节达到目的,我们通过实验发现,当微分环节超过10时,系统的超调如下图所示。

此时系统已经不存在超调,现在只需要解决稳定时间小于2s这个参数即可,我们通过设置积分环节达到这个目的,通过实验发现,当系统的积分环节大于200时,稳定时间小于2s。此时整个系统的波形如下图所示。

-
PID
+关注
关注
35文章
1472浏览量
85487 -
稳态误差
+关注
关注
0文章
8浏览量
2094 -
系统
+关注
关注
1文章
1015浏览量
21332
发布评论请先 登录
相关推荐




 什么是PID算法
什么是PID算法











评论