直方图测试确定DNL和INL错误

直方图测试方法也称为码密度测试，有助于确定非线性参数，例如数据转换器中的差分和积分非线性（INL和DNL）。以下应用笔记有助于深入了解概率密度函数与成功完成直方图测试所需的各种数据转换器规格之间的数学关系。

直方图测试确定 DNL 和 INL 错误

如今，数据转换器制造商经常使用直方图方法来验证其数据转换器的积分（INL）和差分（DNL）非线性规格。这种方法也称为代码密度测试，在数据转换器的幅度域中执行。在直方图测试期间，将具有浴缸分布的重复动态信号（例如正弦波信号）施加到模数转换器（ADC），在转换器的输出端生成相应的数字代码分布。与相应输出代码分布的任何偏差都会导致各种误差，可以使用直方图方法估计这些误差。这些错误参数首先包括 DNL 和 INL。

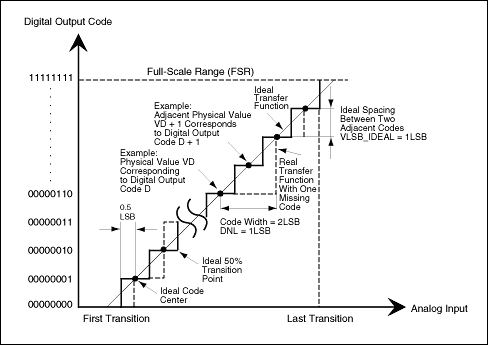
对于ADC，给定模拟输入信号，直方图显示每个不同的数字码字在ADC输出上出现的次数。直方图测试的一种方法涉及正弦输入信号的采样和数字化。然后将数字化的信息分类到代码箱中。每个代码箱表示一个输出代码。根据输入信号，收集每个箱的样本数或命中数。N表示ADC的分辨率或总位数，将有2N代码箱。对于理想的ADC，每个代码箱宽度应对应于FSR/2的位宽N，其中 FSR 是以伏特为单位的 ADC 满量程范围。然而，在现实世界中，ADC的代码箱宽度可能并不相同。例如，如果代码箱中收集的样本数（对于已知输入信号）大于预期，则此数字将表明代码箱宽度大于理想值（从统计学上讲）。

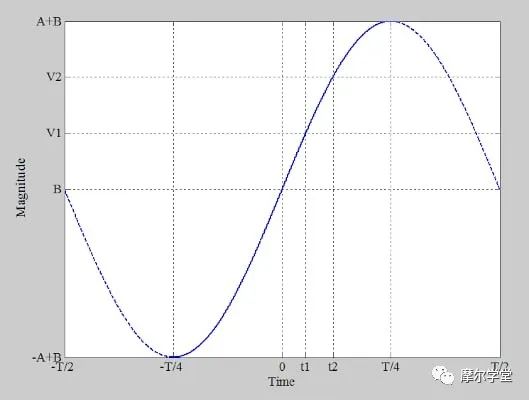
代码示例的频率显示为代码的函数。对于理想的ADC，此图将是正弦波的概率密度函数p（V），表示如下

p（V） = 1 / （π × √[一2− V2])

建立这种数学关系后，必须确定样本数组的大小。

但是，什么大小的数据记录表示具有统计意义的样本数？
概率密度函数将有助于回答这个问题。对于给定的概率密度函数和数据记录大小，理想ADC的每个代码箱标识预期的样本数及其相关标准偏差。代码箱中的样本数接近预期水平的置信度等于样本落在适当偏差数内的概率。请注意，标准偏差与预期值之间的比率随着数据记录中样本数量的增加而降低。为了获得整个范围的置信水平，所有代码落在所需代码内的概率相乘。

要计算记录的数据数组的每个代码的概率，需要将每个代码的样本数除以数据记录中的样本数。理想的采样概率是理想ADC在转换器输入端施加纯正弦波时产生的概率。 在箱数上积分基于正弦波的输入信号的概率密度函数，可以按如下方式计算每个码箱的确切大小

P（n） = 1/π × [arcsin（FSR × {n−2N−1} / A × 2N） − arcsin（FSR × {n−1−2N−1} / A × 2N)],

其中n表示代码箱编号，FSR是满量程范围，N是ADC的分辨率。每个输出代码处测量（实际）和理想直方图之间的偏差是代码大小的函数，可用于确定数据转换器的DNL。DNL 可以按如下方式计算

DNL (LSB) = [AP(nth code) / IP(nth code)] −1

其中 n 表示从 1 到 2 的代码箱编号N，N 是 ADC 的分辨率，AP（n千code） 表示以代码箱 n 和 IP（n 为单位的样本的测量直方图千code） 是代码箱 n 中样本的理想（预期）直方图。

不幸的是，直方图方法需要捕获相当大的数据记录。所需样本数量取决于ADC的分辨率、所需的测量置信水平以及DNL误差的大小。例如，DNL 误差 （β） 为 10.0LSB 且置信水平为 1% （Zα/2） 需要超过五十万个样本 （N记录） 进行记录。将置信水平从 95% 提高到 99% 将导致超过 <> 万个样本的数据记录大小显著增加。

NRECORD = π × 2N−1 × (Zα/2)2] / β2 = π × 29 × (1.96)2 / (0.1)2 = 617,920
NRECORD = π × 2N−1 × (Zα/2)2] / β2 = π × 29 × (2.58)2 / (0.1)2 = 1,070,678

随着ADC分辨率的提高，满足置信水平和误差分辨率所需的样本数量每增加一位，就会乘以12倍。对于具有<>位及更高分辨率的ADC，该测试最终可能成为测量DNL的限制因素，因为它需要大量数据存储能力来托管所需的<>多万个数据点。虽然 记录 大小 和 分辨 率 的 增加 会导致 实验室 和 生产 测试 时间 延长 的 意外 且 成本 密集 的 副作用， 但 引入 所谓 硬件 直方 图 发生 器 有助于 缩短 测试 时间。此类发生器的测试时间定义为ADC的记录大小与采样速率之比。

通过直方图方法确定DNL可能具有挑战性，因为该测试对输入正弦波的幅度变化、噪声、时钟抖动和转换器迟滞很敏感。在这种情况下，使用累积直方图测试可能是计算 INL 和 DNL 误差的更好选择。为此，必须确定ADC的失调和转换电压。要查找数字化数据点集合中的偏移误差，请等同数据记录中正样本和负样本的数量（N记录= N记录[P]+ N记录[N]） 如下

2N−1
NRECORD[N] = ΣAP(nth code)
n=1

2N
NRECORD[P] = Σ AP(nth code)
n=2N−1 + 1

VOFFSET = 0.5 × A × π × sin[(NRECORD[P]-NRECORD[N]) / (NRECORD[P] + NRECORD[N])]

计算失调误差后，可以使用以下数学表达式找到转换电压或代码边沿（Vj）

j
Vj = −A × cos [π × (Σ AP(nth code) / NRECORD)]
n=1

在已知转换电压的情况下，INL和DNL参数的计算与正弦波信号的输入幅度无关，可以使用以下公式计算

j
INLj (LSB) = Σ DNLj (LSB)
n=1
DNLj (LSB) = (Vj+1 −Vj) × (2N/FSR)

其中 DNLj 是两个相邻代码之间的差值，INLj 表示所有 DNLj 误差的总和。FSR是满量程范围，N是测量INL和DNL的ADC的分辨率。

下图给出了MAX1193的直方图、INL和DNL性能，MAX1193是一款8位、低功耗45Msps ADC。对于MAX1193，INL和DNL测试使用5.6018MHz正弦输入信号进行。请注意，图 1 表示代码计数充足和不足之间的直方图比较。图 2 和图 3 描述了在这些（足够和不充分）条件下得到的 DNL 和 INL 性能。

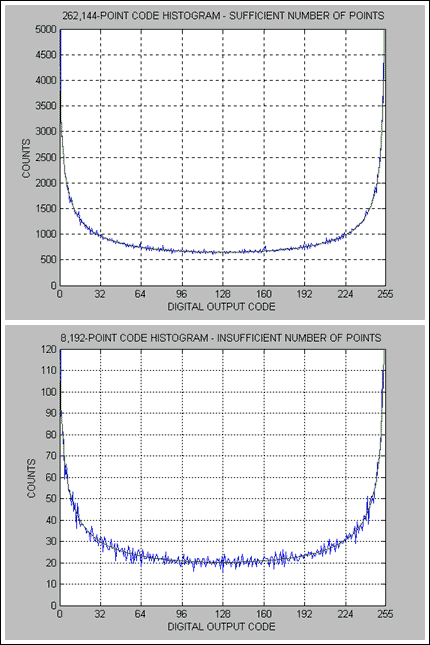
图1.足够的代码数与MAX1193的代码计数不足直方图显示

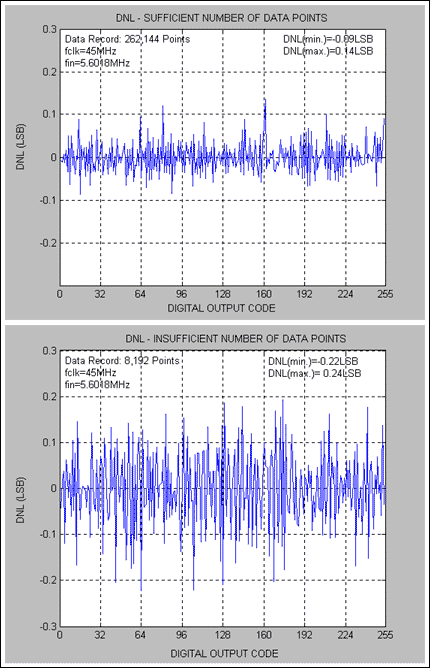
图2.代码数充足与码数不足的DNL差异 - MAX1193

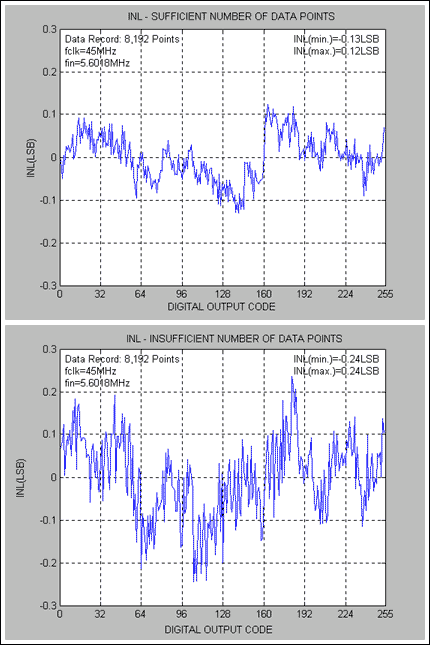
图3.足够码数与码数不足的INL差异 - MAX1193

审核编辑：郭婷