我一直都在这里分享计算机基础知识,比如计算机组成原理、数据结构与算法、计算机网络和操作系统等。
不过偶尔我也想写一下其他的话题,今天就想和你聊聊图像处理的相关知识,因为工作中会用到图像处理,所以就研究了一下。废话不多说,先扔一个目录在这:
**图像卷积
图像梯度
边缘提取
-
Prewitt算子
-
Sobel算子
-
Laplacian算子
平滑去噪
-
高斯滤波
-
均值滤波
-
中值滤波**
文章有点长,看不完可以先收藏。
01
图像卷积
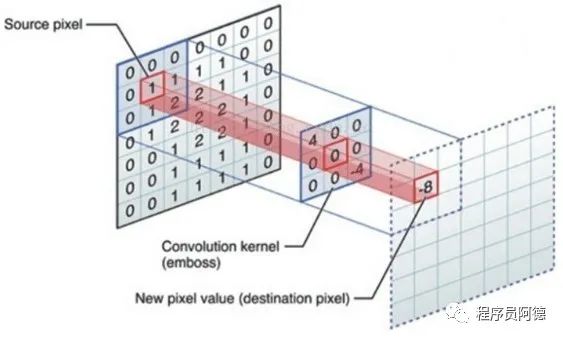
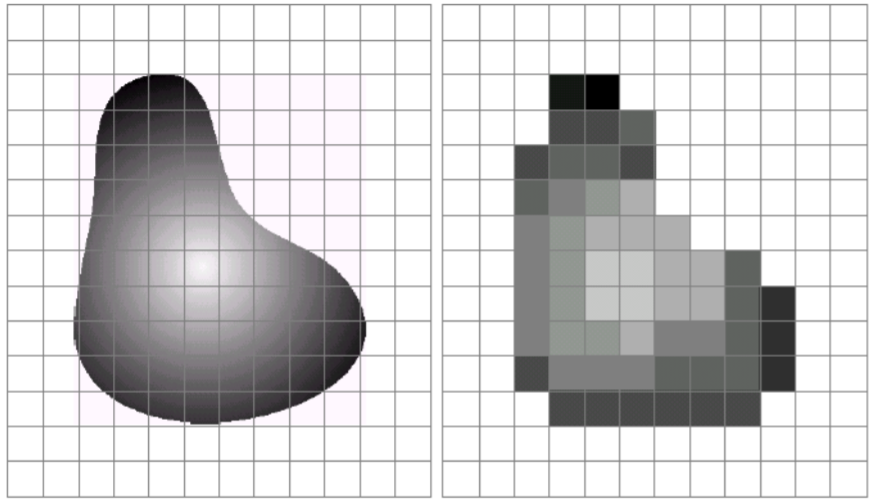
这里有一张图像 f(x,y) 和一个kernel核 w(a,b)。通过核对图像进行卷积
如下图所示:
 这是要做什么呢?先来看看卷积操作是什么意思。
这是要做什么呢?先来看看卷积操作是什么意思。
卷积操作就是对于图像 f(x,y) 中的每个像素,将其作为中心像素,计算它及其邻域像素和 kernel核 w(a,b) 对应位置元素的乘积,然后把结果相加到一起,得到的值就作为该中心像素的新值,这样就完成了一次卷积运算。
如上图所示,原图像中的 1 经过卷积操作,得到新值 -8。
然后将 kernel 向下或向左滑动一位继续计算其他像素的新值,直到遍历完整个图像。
用公式表示卷积运算:
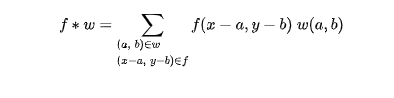
还有一个和类似的概念是 互相关 (Cross-correlation),流程和卷积类似,区别在于卷积在运算前需要把kernel围绕中心旋转180度(即做一次上下翻转(filp)和一次左右翻转),而互相关则不需要。
互相关的公式如下:
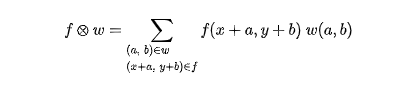
互相关主要用于计算两个图像的相关性(主要用于图像配准)。因为我们平时接触的卷积核大都是关于x轴和y轴对称的,所以卷积和互相关在这种情况下没什么区别。
中心像素在图像的边缘时,没有足够的像素与kernel进行运算,有两个方法来解决:
- 最外面的一圈像素不进行计算,如果图像非常大,丢掉图像边缘的一圈对结果影响不大。
- 比较好的办法是人为地在图像四周插入一圈像素(比如最近邻插值)。
图像的处理结果可能超出值域范围(0-255),则小于0的值视作0,大于255的视作255就行了。
这里的核是什么意思,卷积到底有什么用?别着急,接下来会慢慢介绍。
02
图像梯度
梯度的方向是函数 f(x,y) 变化最快的方向,当图像中存在边缘时,有一些相邻像素的灰度值变化比较大,即一定有较大的梯度值。所以可以求图像的梯度来确定图像的边缘。
分别对图像按照x方向和y方向进行求偏导,得到x梯度图和y梯度图。梯度是矢量,存在幅值和方向,下面这个公式表示了图像的梯度:

梯度方向会取绝对值,因此得到的角度范围是 [0,180°]。
导数的含义就是计算像素灰度值的变化率,对于离散图像而言,在图像上使用一阶差分来计算相邻像素之间的差值,从而得到图像的梯度。
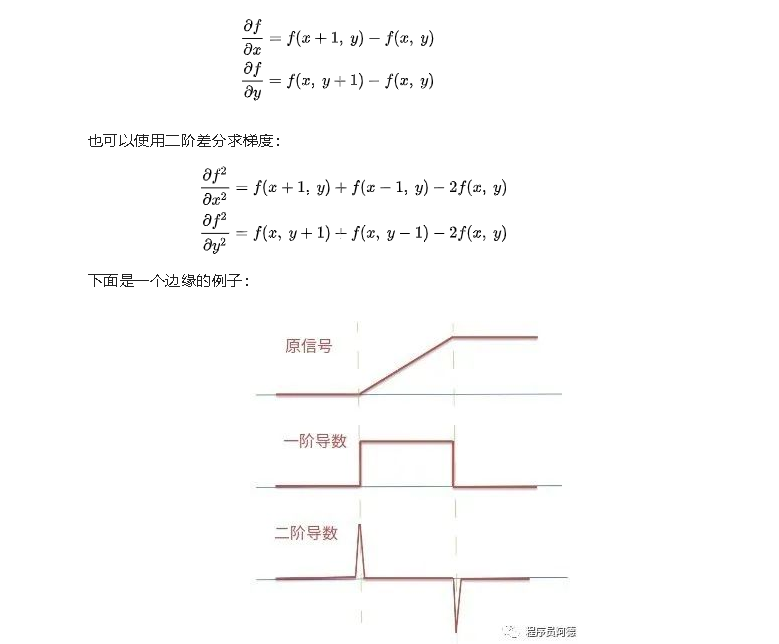 上面是对斜坡区域进行求导,斜坡区域是图像中最常见的区域,因为图片中的大部分边缘都不是突变的而是渐变的。
上面是对斜坡区域进行求导,斜坡区域是图像中最常见的区域,因为图片中的大部分边缘都不是突变的而是渐变的。
对于斜坡区域,一阶导数将斜坡变成了平坦区域即变成了粗线,二阶导数将斜坡变成了两条中间存在平台区域的细线。
关于一阶和二阶导数总结如下:
- 一阶导数在图像中产生较粗的边缘
- 二阶导数对细节更敏感,如细线、噪声等,它提取出来的边缘更细更强(sharp)
- 二阶导数在灰度斜坡和灰度台阶过度处会产生双边沿响应
- 二阶导数的符号可以确定边缘的过渡是从亮到暗还是从暗到亮
- 根据导数提取边缘之前最好对图像做平滑处理,因为导数对噪声比较敏感,尤其是二阶导数
- 二阶导数会强化边缘和其他区域的对比度,但是也会将灰度平滑区域的噪声进行放大,使其更明显
-
图像处理
+关注
关注
27文章
1289浏览量
56725 -
计算机
+关注
关注
19文章
7489浏览量
87873
发布评论请先 登录
相关推荐




 图像处理基础知识 1
图像处理基础知识 1

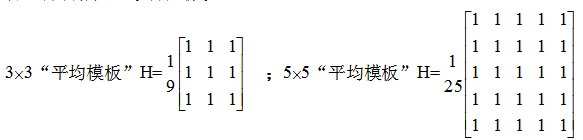










评论