双极性ADC和差分ADC中的失调误差和增益误差

关于模数转换器（ADC），了解双极性ADC和差分ADC中的失调误差和增益误差以及失调误差单点校准。

在上一篇文章中，我们讨论了如何
失调误差可能会影响单极性ADC的传递函数。 考虑到这一点，单极性ADC的输入只能接受正电压。 相比之下，双极性ADC的输入可以处理正电压和负电压。 在本文中，我们将探讨双极性和差分ADC的失调和增益误差规格; 并了解失调误差的单点校准。

传递函数—双极性ADC理想特性曲线

采用失调二进制输出编码方案的理想三位ADC的传递函数如图1所示。

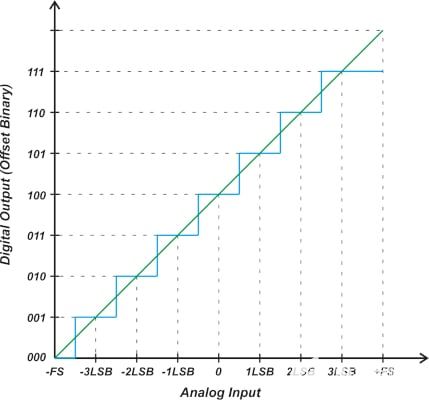
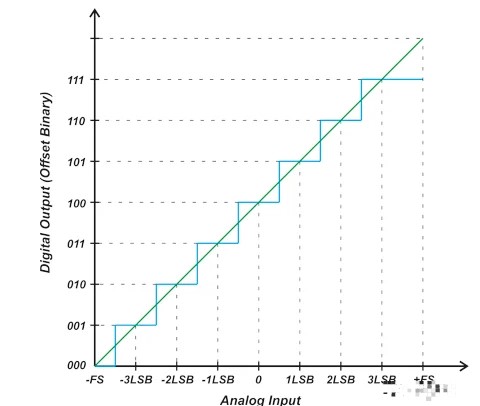
图1. 具有偏移二进制输出编码的理想三位ADC的传递函数，

作为复习，对于偏移二进制系统，中间电平代码的中心（在我们的示例中为100）对应于0 V输入。 低于 100 的代码表示负输入电压，高于 100
的数字值表示正interwetten与威廉的赔率体系 输入。 但是，请注意，垂直轴上的代码序列与单极性ADC的顺序完全相同。 穿过台阶中点的直线为我们提供了ADC阶梯响应的线性模型。

需要注意的另一件事是，上述特性曲线也可以表示具有差分输入的单极性ADC。 由于低于 100 的输出代码表示负值，因此绘制上述传递函数会很有帮助，如图 2
所示。

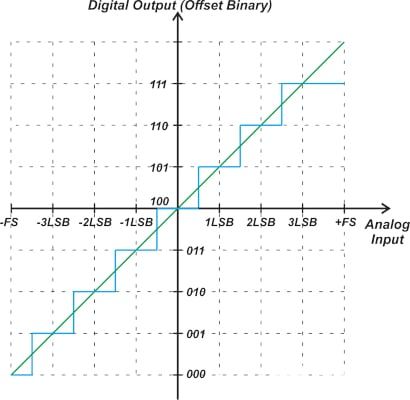
图2. 传递函数显示低于 100 的输出代码。

双极性ADC失调误差

对于采用失调二进制编码方案的ADC，失调误差可以通过比较从100.。.00 到
100.。.01在理想ADC中进行相应的转换。 如图2所示，理想情况下，这种转变应该发生在+0.5 LSB处。 图3所示为失调值为-1
LSB的三位双极性ADC。

请注意，从 100 到 101 的中间电平转换发生在 +1.5 LSB 而不是 +0.5 LSB 处。

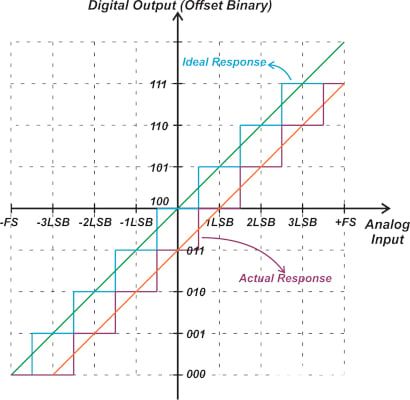
图3. 失调值为-1 LSB的三位双极性ADC的传递函数。

具有正失调的三位双极性ADC如图4所示。

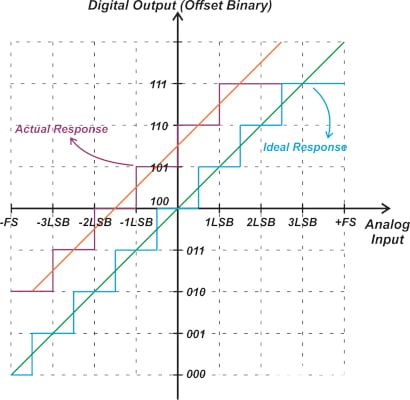
图4. 具有正失调的三位双极性ADC。

在这种情况下，正输入的第一个转换发生在+1 LSB处，从110到111。对于理想ADC，这种转换应在+2.5

LSB处发生。因此，实际传递函数的失调为+1.5 LSB。您还可以通过检查实际传递曲线的线性模型来获得相同的结果，如图 4 中的橙色直线所示。

双极性ADC增益误差

与单极性ADC类似， 双极性ADC的增益误差

可以定义为失调误差被修整后实际的最后一次转换与理想的最后一次转换的偏差。增益误差也可以定义为实际线性模型的斜率与理想直线模型的斜率的偏差。

例如，考虑图5所示的特性曲线。

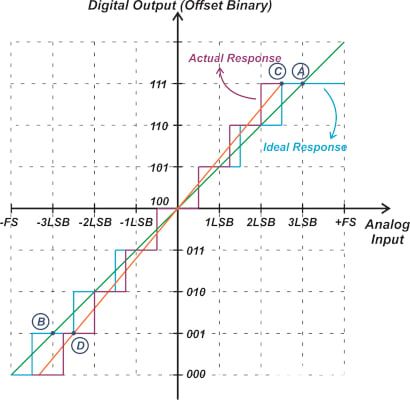
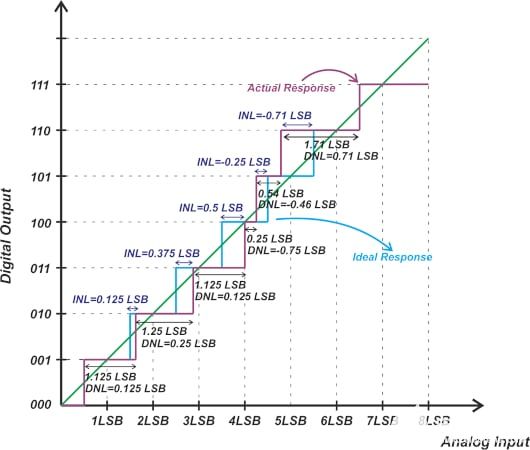
图5. 特性曲线示例

在本例中，点A和C分别比理想响应和实际响应的最后一个跃迁高0.5LSB。同样，在理想和实际传递曲线上分别选择接近负满量程（低于010至001跃迁0.5LSB）的点B和D。穿过A和B的线是理想响应，而穿过C和D的线是系统的实际响应。可以将实际斜率与理想斜率进行比较，以确定增益误差。

在上面的例子中，理想的斜率由下式给出：

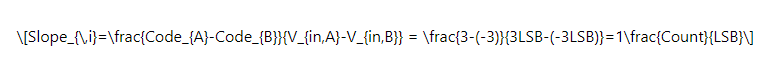
在此等式中，使用输出代码的十进制等效值。另外，请注意代码的标志。正如预期的那样，理想的坡度是一个。测量的斜率可以通过类似的方式找到：

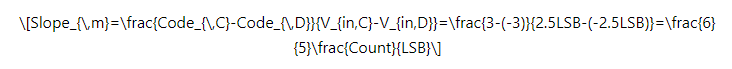
增益误差可通过以下公式定义：

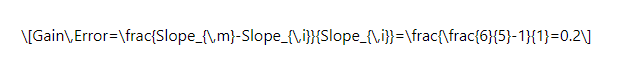
这意味着测量的响应具有20%的增益误差。对于高性能ADC，增益误差可能小到足以以ppm表示。

请记住，在实践中，我们选择查找响应斜率的点不一定是传递函数的端点。根据系统中可用的测试信号和系统线性的输入范围，我们可以选择合适的点来确定传递函数的斜率。例如，在确定满量程值为3V的ADC的斜率时，系统中已有的精确1.5 V输入可能被认为足够接近正满量程值。

失调和增益误差导致输入和输出值未使用。

对于单极性和双极性ADC，失调误差会导致未使用的输入范围和未使用的输出代码。图 6 显示了负偏移如何将输入范围的下限限制为高于 -FS的值。如果偏移为负，则可能也不会使用低于标称最大代码的输出代码范围。

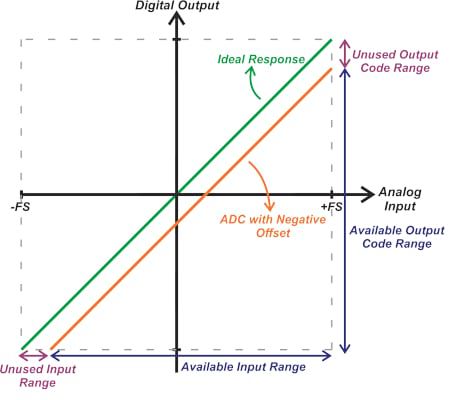
图6. 显示负偏移如何将输入范围的下限限制为高于 -FS 的值的图形。

正如您可能想象的那样，失调误差将以类似的方式影响单极性ADC的范围。例如，考虑一个单极性12位ADC，其满量程电压为2.5 V，失调为-8

mV。这相当于大约 -13 LSB 的偏移量。理想的直线响应向下移动13 LSB。因此，如图7所示，输入模拟范围减小13 LSB（或8

mV），并且不使用最后13个输出代码。

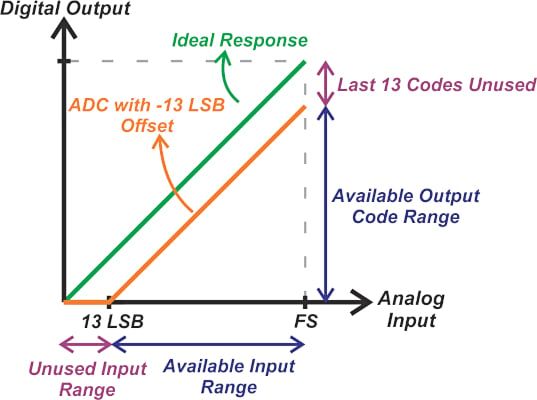
图7. 显示输入模拟范围减少 13 LSB 的图表。

请务必记住，更高分辨率ADC中的相同失调电压会导致更大的未使用代码范围。例如，FS = 2.5 V的16位ADC中相同的-8 mV失调对应于约-210

LSB。在这种情况下，不使用最后 210 个输出代码。图8显示了正失调对ADC输入和输出范围的影响。

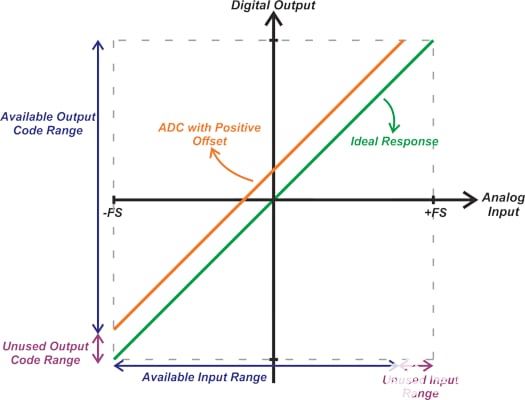
图8. 正失调对ADC输入和输出范围的影响。

在这种情况下，不使用输出代码范围下端的多个代码，并且在小于+FS的输入电平下达到最大ADC输出。正增益误差会限制两端的输入范围，如图9所示。

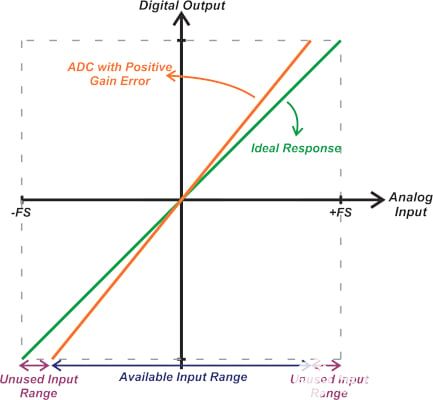
图9. 显示正增益误差如何限制两端输入范围的图表。

类似地，负增益误差会导致标称范围两端出现未使用的输出代码（图 10）。

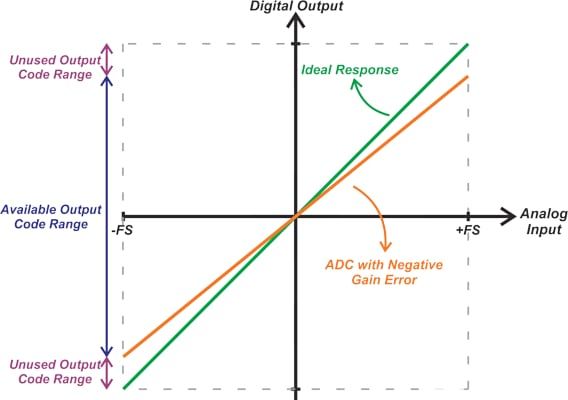
图 10. 负增益误差如何导致标称范围两端的输出代码未使用。

现在我们已经熟悉了ADC中的失调和增益误差概念，我们可以深入讨论这两个误差项的校准。

ADC增益和失调校准

失调和增益误差可以在数字域中轻松校准。为此，应向ADC施加精确的模拟输入，以确定实际响应。在已知实际响应的情况下，可以在数字域中校正ADC输出代码，以匹配理想响应。

由于给定的ADC代码与单个模拟输入值不对应，因此实际ADC响应只能通过测量代码转换来确定。这需要一个可以产生不同电压电平的精密电源。图 11

显示了一个可用于确定代码转换的测试设置。

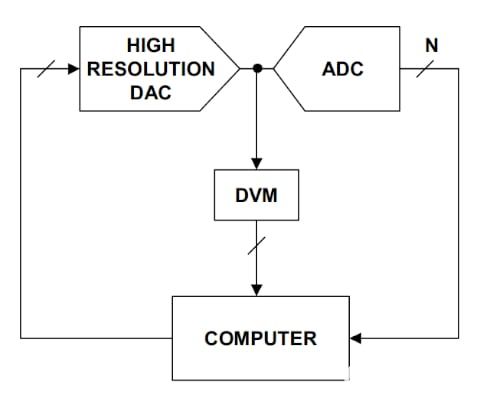
图 11. 用于确定代码转换的示例测试设置 图片由 ADI公司。

在这种情况下，高分辨率 数模转换器 （DAC） 用于在 ADC

输入端产生不同的电压电平。DAC的精度应明显高于被测ADC。此外，DAC输出端的电压表可精确测量发生代码转换时的电压电平。对电压表和ADC的输出进行处理，以确定失调和增益误差以及ADC的非线性度。这种基于

PC 的方法可以使用 数字信号处理 威廉希尔官方网站 ，例如 信号平均，以减少ADC噪声对测量的影响。

在许多应用中，例如传感器测量系统，不可能使用上述设置来测量代码转换。在这些情况下，系统中可能只有一个或两个精密电压电平可用，从而实现单点或两点测量。这些测试只能近似于实际响应，不能完全消除失调和增益误差。但是，它们仍然是可以显著降低失调和增益误差的有效方法。

偏移校准—单点校准

单点校准测量传递函数上单个点的ADC响应，并利用结果来降低失调误差。地电位是单点校准的准确、常用的测试输入，因为它已经在系统中可用。作为应用此方法的示例，考虑响应如图

3 所示，为方便起见，下面重复该响应，如图 12 所示。

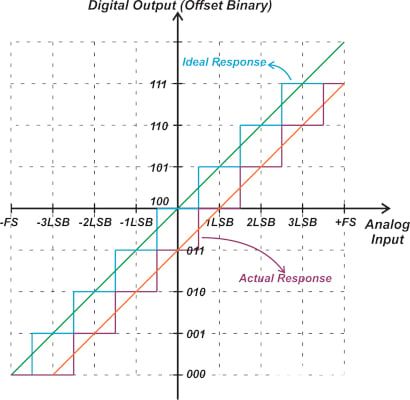
图 12. 重复图3显示了失调值为-1 LSB的三位双极性ADC的传递函数。

如果我们对该ADC施加零伏电压，则输出为011。将此值与理想值100进行比较，我们可以确定ADC的失调为-1 LSB。另一个示例如图 13

所示。

图 13. 示例显示对 ADC 施加零伏电压后 -1 LSB 的 ADC 失调。

在这种情况下，从 010 到 011 的转换发生在零伏以下。再次将输入短路到地面会产生 011。基于这种单点测量，ADC失调为-1

LSB。但是，考虑到代码转换，我们观察到实际偏移量为 -1.5 LSB。如您所见，对于单点测量，确定偏移的误差可能高达±0.5

LSB。尽管如此，此错误在大多数应用程序中都是可以接受的，特别是考虑到这种方法具有最低的成本和复杂性。单点测量无法确定增益误差。

一旦确定失调，我们可以通过从每个ADC读数中减去失调来补偿它。通过地电位进行的单点校准只能与双极性或差分输入ADC一起使用。对于单极性ADC，负失调会导致标称输入范围下限处出现未使用的输入值。下面描述的示例（图

14）进一步阐明了此问题。

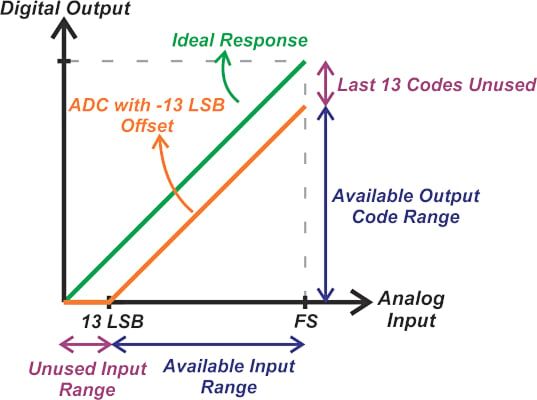
图 14. 显示负偏移的示例导致标称输入范围下限的未使用输入值。

在这种情况下，ADC的失调为-13
LSB。 但是，对输入施加零伏会产生全零输出代码，导致零伏的偏移测量不正确。 这就是为什么对于单极性ADC，我们需要ADC可用输入范围内的精密电压来测量和校准失调误差。