前言

众所周知，增量式SD-ADC相比传统结构而言，需要在每次测量开始之前进行复位，以此清零积分器积分电容上的剩余电荷以及数字滤波器中寄存器。然后，在ADC连续转换时，清零这一操作需要额外操作一次。如果不进行清零直接进行转换，ADC的精度会损失多少？本文针对这个问题进行了Matlab建模，分析了在两种常用数字滤波器，级联积分滤波器（CoI）和SINC滤波器下这一情况的影响。

调制器及测试平台的Matlab实现

本文Matlab建模了一个常用的二阶Sigma-Delta调制器模型，在这个模型中没有进行系数缩放，具体代码如下：

clear
format long

Vref=2.5;
M=256; % Sinc滤波器抽取率
L=3;   % Sinc滤波器阶数
N=10000; % 测试的直流输入点数

for j=1:N;
Vin(j)=3/N*j-1.5;

% Second_order SD Modulator
Vout1=0;
Vout2=0;
Vout1(1)=0;%rand(1)*5-2.5;
Vout2(1)=0;%rand(1)*5-2.5;
bs=0;
for i=2:M*L;
    if bs(i-1)>0.5;
        Vout1(i)=Vout1(i-1)+(Vin(j)-Vref);
        Vout2(i)=Vout2(i-1)+Vout1(i-1)+(Vin(j)-Vref)*2;
    else
        Vout1(i)=Vout1(i-1)+(Vin(j)+Vref);
        Vout2(i)=Vout2(i-1)+Vout1(i-1)+(Vin(j)+Vref)*2;
    end

    if Vout2(i)>0;
        bs(i)=1;
    else
        bs(i)=0;
    end
end

Dout1(j)=sinc3_filter(M,L,bs);
Dout2(j)=coi_filter(M*L,bs);
end

E_sinc=Vin-(Dout1*5-2.5);
E_coi =Vin-(Dout2*5-2.5);
figure(1)
plot(Vin,E_sinc,'r');
title('使用SINC3滤波器的转换误差')
figure(2)
plot(Vin,E_coi,'b');
title('使用CoI滤波器的转换误差')

这个代码实现的功能包括：

• 一个二阶单比特量化的Sigma-Delta调制器；
• 产生N个从-1.5~1.5的直流值输入调制器；
• 分别使用Sinc3滤波器和CoI滤波器对调制器输出进行处理；
• 计算ADC在两种滤波器下分别的转换误差。

其中，两种滤波器Matlab函数的实现代码分别为：

Sinc3滤波器

function Dout=sinc3_filter(M,L,bs)

sigma1=0;
sigma2=0;
sigma3=0;
delta1=0;
delta2=0;
delta3=0;
sigma3_reg=0;

for i=1:length(bs)
  sigma1=sigma1+bs(i);
  sigma2=sigma2+sigma1;
  sigma3=sigma3+sigma2;
    delta1_temp=sigma3-sigma3_reg;
    delta2_temp=delta1_temp-delta1;
    delta3_temp=delta2_temp-delta2;
  if(mod(i,M)==0)
    sigma3_reg=sigma3;
    delta1=delta1_temp;
    delta2=delta2_temp;
    delta3=delta3_temp;
  end
end

Dout=delta3/M^3;
end

CoI滤波器

function Dout=coi_filter(N,bs)

sigma1=0;
sigma2=0;

for i=1:N
  sigma2=sigma2+sigma1;
  sigma1=sigma1+bs(i);
end
Dout=sigma2/(N*(N-1)/2);

end

复位/不复位时两种滤波器的转换误差对比

存在复位时，在代码中每次转换开始之前将两个积分器的输出的初值设置为0，如下代码所示：

Vout1(1)=0;
Vout2(1)=0;

这种情况下，两种滤波器的转换误差如下图所示：

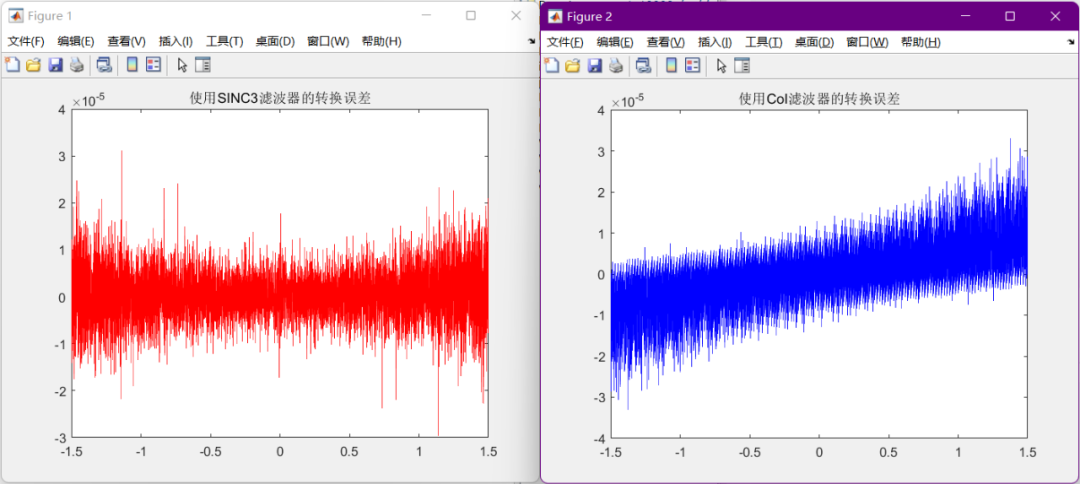
上图中使用两种滤波器的转换误差几乎相近，这与文献[1]中的结论相符，即：在相同的转换时钟周期下，Sinc3滤波器可以实现与CoI几乎相同的转换误差。

不复位时，调制器的积分器1和积分器2的输出会保持为上一次结束时的终态值，实际中这一值会和输入电压大小，热噪声等调制器的非理想因素相关，因此很难在模型中根据原理给出。为了简便起见，本文模型通过产生一个±VREF的随机数赋给积分器1和积分器2的输出初态来实现近似的效果，代码如下所示：

Vout1(1)=rand(1)*5-2.5;
Vout2(1)=rand(1)*5-2.5;

这种情况下，两种滤波器的转换误差如下图所示：

如上图所示，不复位时，使用sinc3滤波器并未使转换精度降低太多，而使用CoI滤波器转换精度急剧下降。这是因为两者对输出码处理的权重不同导致的。对Sinc3滤波器而言，在假设转换周期数为N，那么第一个输出码的权重为1，所有输出码权重和为(N/3) ^3^ ，因此第一个输出码对最终输出数据影响的比重为：1/((N/3) ^3^ )。而对CoI滤波器而言，第一个输出码的权重为(N-1),所有输出码权重和为N*(N-1)/2，因此第一个输出码对最终输出数据影响的比重为：2/N. 当不进行复位操作时，直接的影响为第一个输出码（或前几个输出码）所携带的量化噪声很大，而相比采用CoI滤波器而言，采用Sinc3滤波器时第一个输出码的比重小了很多，因此这个因为没有复位造成的超大量化噪声被更好地稀释，从而对输出码的影响相比采用CoI滤波器急剧降低，基本可以忽略不复位的影响。

（感兴趣的读者可以进一步证明，第一级积分器不复位对CoI滤波器的影响比第二级积分器不复位的影响大很多。）

总结

由上述模型可以发现，设计增量式Sigma-Delta调制器时，如果采用Sinc滤波器，那么即使在开始转换的时候不进行复位，积分器仍然保存上次转换结束所残余的输出值，也不会对输出结果造成太多的误差。因此，如果设计者所设计的增量式SD-ADC采用了Sinc滤波器，那么可以不设计额外的复位操作，尤其是连续转换时，这样仍然不会影响ADC的精度。