为什么数学家研究纽结？

纽结理论（knot theory）已经超越了抽象的数学好奇心，推动了数学及其他领域的许多发现。

纽结理论最初是为了理解宇宙的基本构成。1867年，当科学家们急切地试图找出可以解释所有不同种类物质的方法时，苏格兰数学家和物理学家彼得·格思里·泰特（Peter Guthrie Tait）向他的朋友和同胞威廉·汤姆森爵士（Sir William Thomson）展示了他用于产生烟圈的设备。汤姆森——后来成为开尔文勋爵（与热力学温标同名）——被环迷人的形状、稳定性和相互作用所吸引。他的灵感将他引向了一个令人惊讶的方向：也许，他想，就像烟圈是空气中的漩涡一样，原子是发光以太中结成纽结的涡旋环，物理学家曾认为，光通过以太这种无形介质传播。

虽然这个维多利亚时代的想法现在听起来可能很荒谬，但这并不是一个轻率的研究。这个漩涡理论有很多值得借鉴的地方：纽结的多样性，每个纽结略有不同，似乎反映了许多化学元素的不同性质。涡旋环的稳定性也可能提供原子所需的持久性。

涡旋理论在科学界获得了关注，并激发了泰特开始将所有纽结制成表格，创造了他希望等同于元素周期表的东西。当然，原子不是纽结，也没有以太。到1880年代后期，汤姆森逐渐放弃了他的涡旋理论，但那时泰特被他的纽结的数学优雅所吸引，他继续他的制表项目。在这个过程中，他建立了纽结理论的数学领域。

我们都熟悉纽结——它们让我们的脚能穿上鞋，让船固定在码头上，让登山者能从下面的岩石上来。但这些纽结并不完全是数学家（包括泰特）所说的纽结。虽然缠绕起来的线团可能看起来打了结，但总是可以解开它。要打一个数学纽结，你必须将线的自由末端插在一起以形成一个闭环。

因为纽结像绳子（或译为弦）一样灵活，数学家将纽结理论视为拓扑学的一个子领域，即对可延展形状的研究。有时可以解开一个纽结，让它变成一个简单的圆，我们称之为“（可）解纽结”（unknot）。但更多时候，解开一个纽结是不可能的。

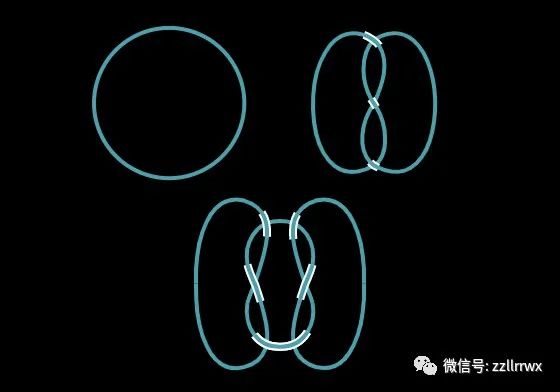
三个简单的纽结（从左上角顺时针方向）：（可）解纽结、三叶纽结（trefoil）和方形纽结。

纽结也可以组合形成新的纽结。例如，将称为三叶草的简单纽结与其镜像结合会产生一个方形纽结。（如果你加入两个相同的三叶纽结，你就得到一个奶奶纽结（granny knot）。

 

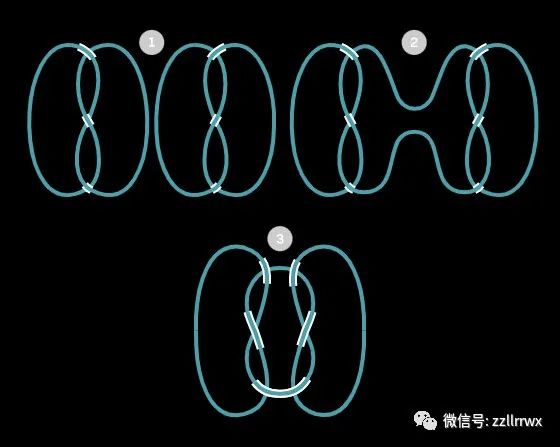
将三叶纽结及其镜像连接起来，形成一个方形纽结。 使用数字世界的术语，数学家说三叶纽结是素纽结，方纽结是（复合、合成）合纽结，（可）解纽结既不是素的，也不是合的（就与数字1一样，既不是素数，也不是合数）。这个类比在1949年得到了进一步的支持，当时霍斯特·舒伯特（Horst Schubert）证明了每个纽结要么是素纽结，要么可以唯一地分解为素纽结。

创建新纽结的另一种方法是将两个或多个纽结交织在一起，形成一个链。波罗密欧环（Borromean ring）之所以如此命名，是因为它们出现在意大利Borromeo波罗密欧家族的徽章上，它就是一个简单的例子。

 

为了形成Borromean环，三个环必须相互连接，而没有两个单独的圆环相连。

汤姆森和泰特并不是第一个以数学方式看待纽结的人。早在1794年，卡尔·弗里德里希·高斯（Carl Friedrich Gauss）就在他的个人笔记本上写下并画了纽结的例子。高斯的学生约翰·利斯廷（Johann Listing）在他1847年的专著《拓扑学的初步研究》（Vorstudien zur Topologie）中写到了纽结——这也是拓扑学一词的起源。

但泰特是第一个研究纽结理论基本问题的学者：所有可能的纽结的分类和制表。通过多年的艰苦工作，仅使用他的几何直觉，他就发现并对所有素纽结进行了分类，当投影到平面上时，最多有七个交叉点。

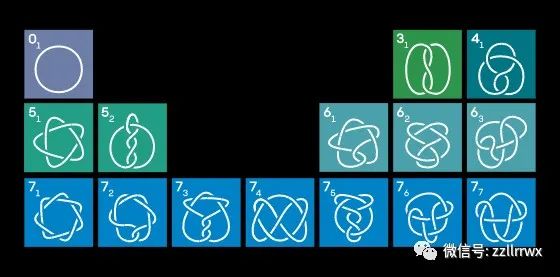
以元素周期表的样式排列的可解纽结和所有具有七个或更少交叉（忽略镜像）的素纽结。

在19世纪末，泰特得知另外两个人——托马斯·柯克曼牧师（Rev. Thomas Kirkman）和美国数学家查尔斯·利特尔（Charles Little）——也在研究这个问题。在他们的共同努力下，他们将所有素纽结分类为多达 10 个交叉点，其中许多具有 11 个交叉点。令人惊讶的是，他们10个及10个以内交叉点的纽结表是完整的：没有错过任何纽结。

值得注意的是，泰特、柯克曼和利特尔在没有后来几年中发现的定理和威廉希尔官方网站 的情况下取得了如此多的成就。但对他们有利的一件事是，大多数小纽结都是“交替的”，这意味着它们有一个投影，其中交叉点表现出一致的上-下-上-下模式。

交替纽结具有比非交替纽结更容易分类的特性。例如，很难找到任何纽结投影的最小交叉数。但是泰特多年来错误地认为所有的纽结都是交替的，他推测了一种判断是否找到最小数字的方法：如果一个交替投影没有可以通过翻转部分纽结即可消除的交叉点，那么它一定是交叉次数最少的投影。

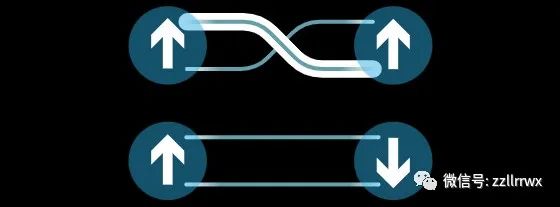
特称任何可以通过翻转部分纽结来消除的交叉点都是“无价值的”（nugatory）或无关紧要的。

泰特关于交替纽结的另外两个猜想最终都是真的。然而，这些著名的猜想直到1980年代末和90年代初，使用沃恩·琼斯（Vaughan Jones）于1984年开发的数学工具后，才被证明。琼斯因在纽结理论方面的工作而获得菲尔兹奖。

不幸的是，交替的纽结只能带你走这么远。一旦我们进入有八个或更多交叉的纽结，非交替纽结的数量就会迅速增加，这使得泰特的威廉希尔官方网站 变得不那么有用。

这个8-交叉纽结，作为真爱之人的纽结，不能用交替的投影来绘制。

所有 10-交叉纽结的原始表是完整的，但泰特、柯克曼和利特尔重复计算了。直到1970年代，曾在普林斯顿大学研究纽结理论的律师肯尼斯·佩尔科（Kenneth Perko）才注意到其中两个纽结是彼此的镜像。为了纪念他，他们现在被称为Perko对（Perko pair）。

这两个 10-交叉纽结，称为 Perko 对，是同一个纽结。

在过去的一个世纪里，数学家们发现了许多聪明的方法来确定纽结是否真的不同。从本质上讲，这个想法是识别一个不变量——与节点相关的属性、数量或代数实体，通常可以简单地计算。（这些属性具有可着色性（colorability）、桥数（bridge number）或 翻滚（writhe） 等名称。有了这些标签，数学家现在可以很容易地比较两个纽结：如果它们在任何给定的属性上不同，那么它们就不是同一个纽结。然而，这些性质都不是数学家所说的完全不变量，这意味着两个不同的节点可能具有相同的性质。

由于所有这些复杂性，纽结的制表仍在进行中也就不足为奇了。最近，在 2020 年，本杰明·伯顿（Benjamin Burton）将所有多达 19 个交叉的素纽结进行了分类（有近 3 亿个） https://drops.dagstuhl.de/opus/volltexte/2020/12183/ 。

传统的纽结理论只在三维空间才有意义：在二维中，只有可解纽结是可能的，而在四维中，额外的空间允许纽结自行解开，所以每个纽结都与可解纽结相同。

然而，在四维空间中，我们可以给球面打结。为了理解这意味着什么，想象一下以规则的间隔切割一个普通的球面。这样做会产生圆圈，就像纬度线一样。然而，如果我们有一个额外的维度，我们可以把球面打结，所以这些切片，现在是三维的，而不是二维的，可以成为纽结。

当我们在三维空间中切一个球面时，我们得到的是圆。但是在四维空间中打结的球面的切片可能是纽结。

这个想法是纽结理论最近最大的结果之一。2018年，当时的研究生丽莎·皮奇里洛（Lisa Piccirillo）解决了50年前的问题，即约翰·康威（John Conway）首次发现的11-交叉纽结。这个问题与一种叫做sliceness（可切性）的属性有关。正如我们所看到的，当我们在四维中切开一个打纽结的球面时，我们会在三维空间中获得一个纽结或链。有时我们可以从一个漂亮的光滑纽结球面中获得给定的纽结，但对于其他纽结，球面必须像一张废纸一样打结和皱缩。从本质上讲，Piccirillo证明了康威的纽结属于后一种类型。用威廉希尔官方网站 术语来说，她证明了它不是“光滑切片”（smoothly slice）。

Lisa Piccirillo证明，康威纽结并不“光滑”。

几个世纪以来，纽结理论在数学领域纵横交错。它最初是数学的一个应用领域，汤姆森试图用纽结来理解物质的构成。随着这个想法的消失，它变成了纯数学的一个领域，是拓扑学这个有趣且仍然不实用的领域的一个分支。但近年来，纽结理论再次成为数学的一个应用领域，因为科学家利用纽结理论的思想来研究流体力学、电动力学、纽结分子如DNA等。幸运的是，当科学家们忙于研究其他事情时，数学家们正在建立纽结目录和解开它们秘密的工具。

审核编辑：刘清