平面度的测量及管控是我们产品最常见的一个规格,平常我们只是用设备测出产品平面度的数据,对其测试原理也是一知半解,当客户对我们测试的数据产生质疑的时候,我们若不能合理解释,则很难有效说服客户;得不到客户的信任,则我们的工作也很难进行下去。
平时,我们总简单认为,平面度的测试就是用镜头到产品的最高点减去最低点即可,事实上,这样的计算方法是错误的计算方法!平面度的本质是关心被测平面上各被测点之间的相互差异,并不关心各被测点和其他特征之间的差异。如果用高度差算,这个高度差会把上表面与下底面的平行误差也引进来了,而这个平行误差原本和上表面的平面度误差无关。多余引入的平行误差会使我们的数据大于产品的实际表现,及测出的结果偏高。
今天我们详细介绍下3次元设备是如何利用点位去拟合基准平面从而得出产品的平面度数值的,其主要用到的数学原理就是最小二乘法,期间会有一些线性代数的矩阵加减乘除,矩阵的转置等。不过我们可以直接用Excel表格来计算,将会简单许多。
最小二乘法的拟合基准平面主要分为如下几个步骤,我们将通过一个案例来逐步讲解:
1. 拟合出最小二乘平面;
2. 找到最小二乘平面两侧的最远采集点到该最小二乘平面的距离H1,H2(如下图);
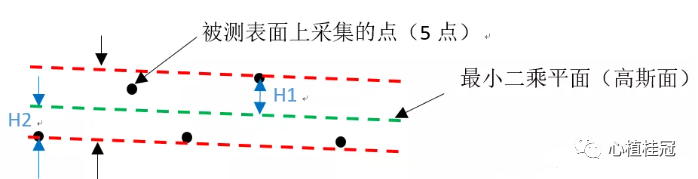
3. 通过计算出来的最远点的距离H1和H2相加,即平面度的实测值;因为我们计算出的点到平面的距离有方向性,所以直接采用最大的距离减去最小的距离就是平面度的结果了。
01
拟合最小二乘平面
我们首先在产品下表面上采了9个点,点坐标如下图: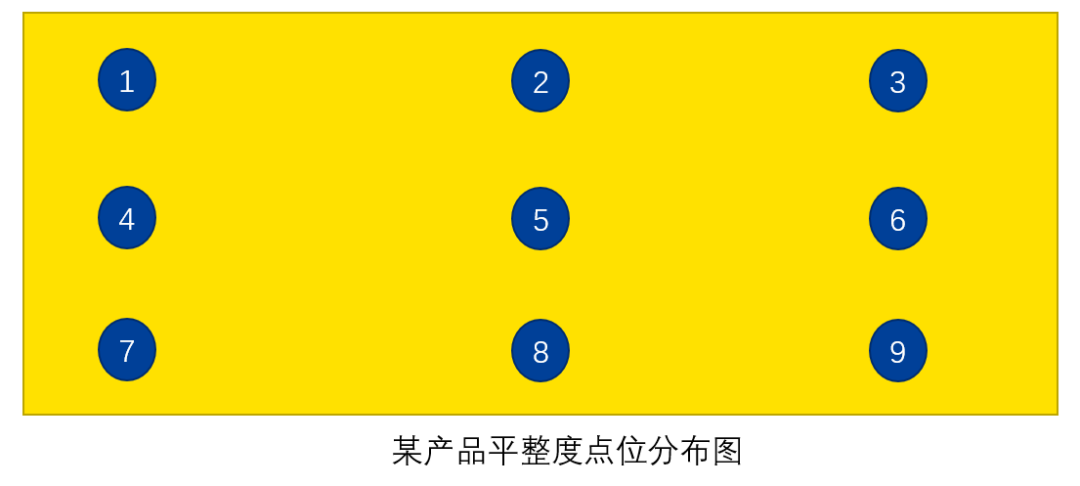
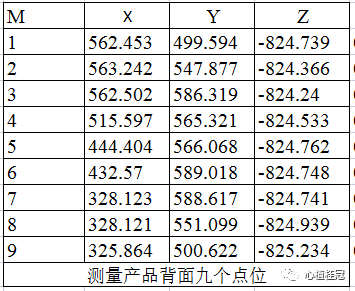
平面方程的公式为:z=ax+by+c 平面方中,a,b,c是平面方程的参数,只要知道a,b,c,我们就知道最小二乘法拟合出来的基准平面了。同样的方法,把D1,D2...D9的x,y,z坐标值分别代入平面方程,可以得到下面的超定方程组:
接下来的思路是如何把它转化成矩阵方程,如下:

则平面方程z=ax+by+c就可以写成矩阵方程Ax=b 显然A是已知的系数矩阵(代入坐标值就已知),x包含3个未知数a,b,c, b也是一个数据已知的矩阵(所有的已知z)。我们就可以套公式啦。
我们将原始的数据整理成A和b, 然后利用Excel的函数:
x=MMULT(MMULT(MINVERSE(MMULT(TRANSPOSE(A),A)),TRANSPOSE(A)),b)可以直接求出a,b,c。
Excel的具体数据如下: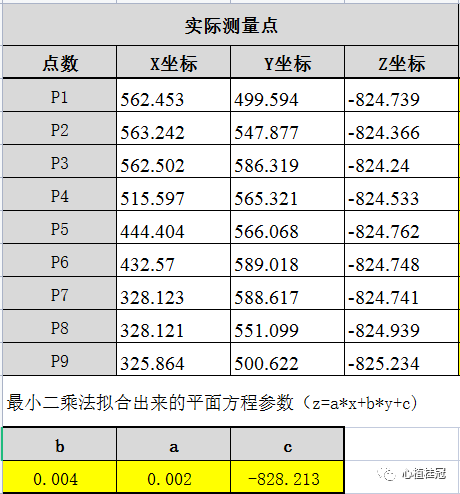
根据上表的计算,可以得到基准A的方程是:
z=0.02x+0.04y+(-828.213)
为了方便后边直接套用公式,需要将上面这个基准平面的方程直接转化标准平面方程:Ax+By+Cz+D=0, 转化后为:
0.02x+0.04y+(-z)+(-828.213)=0
显然,标准平面方程,我们可以得出: A=0.02, B=0.04,C=-1, D=-828.213, 这四个标准平面方程的参数在算距离的时候,马上要用到的。
02
找到点到最小二乘平面的距离
然后再求被测要素上每一个点到该基准面的距离,就可以算出轮廓度。这里需要利用点到面的距离公式(A,B,C,D四个参数刚好可以在这里用上):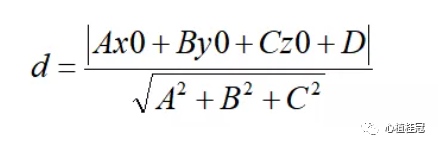
将被测要素每点的坐标代入上面点到面的公式,用点的实际坐标代该公式中的x0,y0,z0。计算出每点到基准面的距离,最后可以计算出轮廓度(按照ISO标准)。最后的计算结果参考下面的表格结果:
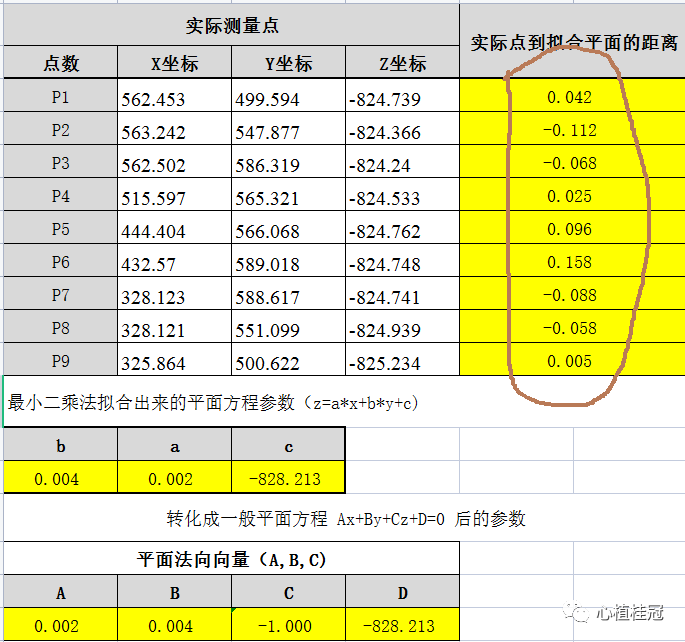
03
计算平面度
最后只要计算出被侧面上每个点到基准面的距离,用最远距离减去最近距离就是平行度了。结果如下图: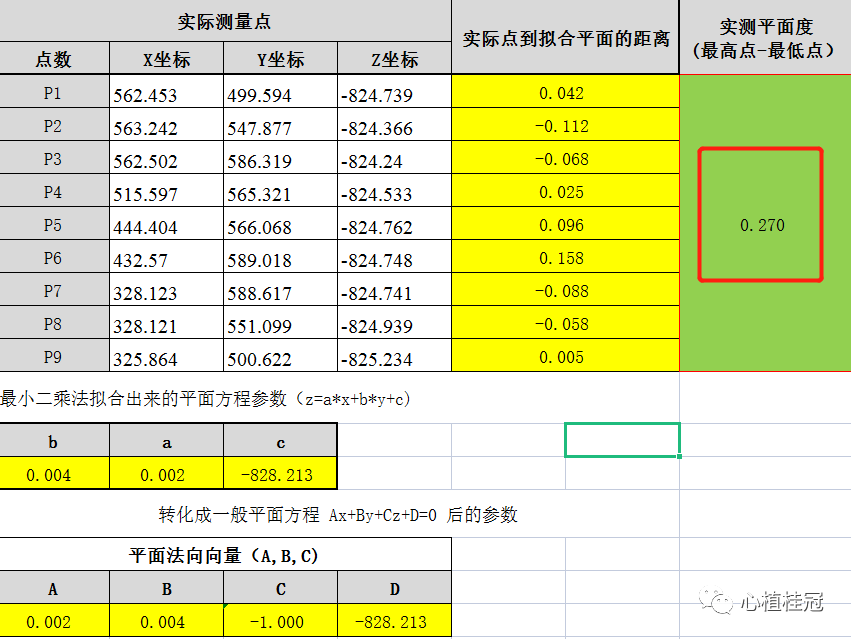
我们3次元实测结果如下图:
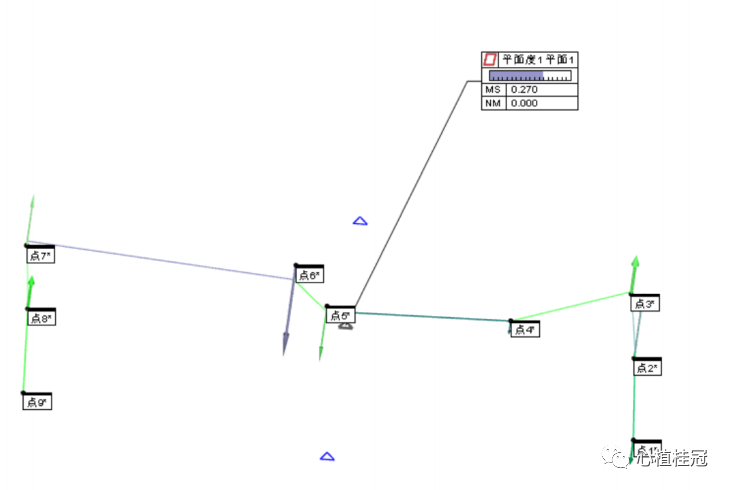
理论计算值与实测值结果一致,可见我们的理论计算是正确的。
04
结束语
本文主要讲述了在已知被测平面上几个点P的具体坐标的前提下,如何用Excel计算该面的平面度误差的操作原理和方法。
本文分为三个部分进行讲解,
1.计算平面度的基本原理,首先将已知点拟合成一个平面,再计算每个点到该平面的距离,距离的总宽度即表示平面度。
2.如何利用Excel的函数Linest()拟合出最小二乘平面以及具体的参数设置。
3.用Excel具体的计算过程和实现办法。
审核编辑:刘清
-
最小二乘法
+关注
关注
0文章
22浏览量
8447
原文标题:3次元测量平面度原理—最小二乘法
文章出处:【微信号:心植桂冠,微信公众号:心植桂冠】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
ADS9234R这个AD的寄存器如何配置,需要用到哪几个引脚?
用TPA3136典型应用电路波形异常,从哪几个方面寻找问题?
工艺仿真可以分为哪几个方面?
二极管的伏安特性分为哪几个区
TAS2505-Q1的MCLK, WCLK, DIN, BCLK这几个PIN,对应的mcu这边的哪几个pin?
自动化威廉希尔官方网站 主要包括哪几个方面的内容
ADuC845来画PCB的话,需要引出来哪几个脚来烧录?TXD和RXD吗?
一个成熟的PCBA设计通常包含哪几个方面?
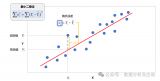
机器学习六大核心算法深度解析
浅析基于matlab Parameter Estimation Tool工具箱的电池参数





 最小二乘法的拟合基准平面主要分为哪几个步骤
最小二乘法的拟合基准平面主要分为哪几个步骤










评论