作者:Chao Qin1 Haoyang Ye Christian E. Pranata, Jun Han, Shuyang Zhang, and Ming Liu
来源:ICRA 2020
摘要
LINS是以滤波为主的IMU、激光雷达紧耦合的激光SLAM算法。该算法的主要创新点就是用以 IESKF(即迭代误差卡尔曼)为框架,融合 IMU 与激光雷达。该算法于发表于 2020 年 ICRA, 由于网上已经有些同学对算法做了介绍,一些基础的知识本文不再赘述,本文将详细围绕以下两个问题介绍,希望对读者理解算法有所帮助: 1、LINS 是如何将激光观测融入滤波框架的? 2、滤波框架与优化框架有何不同?
算法框架
为了讲述通畅还是先介绍下 LINS 算法的主要框架,算法流程图如下:
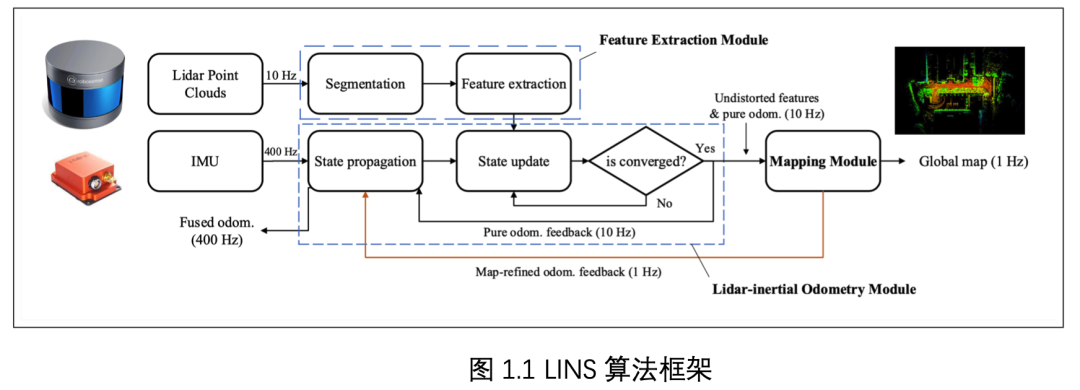
结合代码不难发现,算法的特征提取、以及 Mapping 部分都是直接沿用了 Lego-Loam 算法的,不再赘述。算法的核心创新点为前端激光里程计部分,对应代码的 lins_fusion_node 节点。
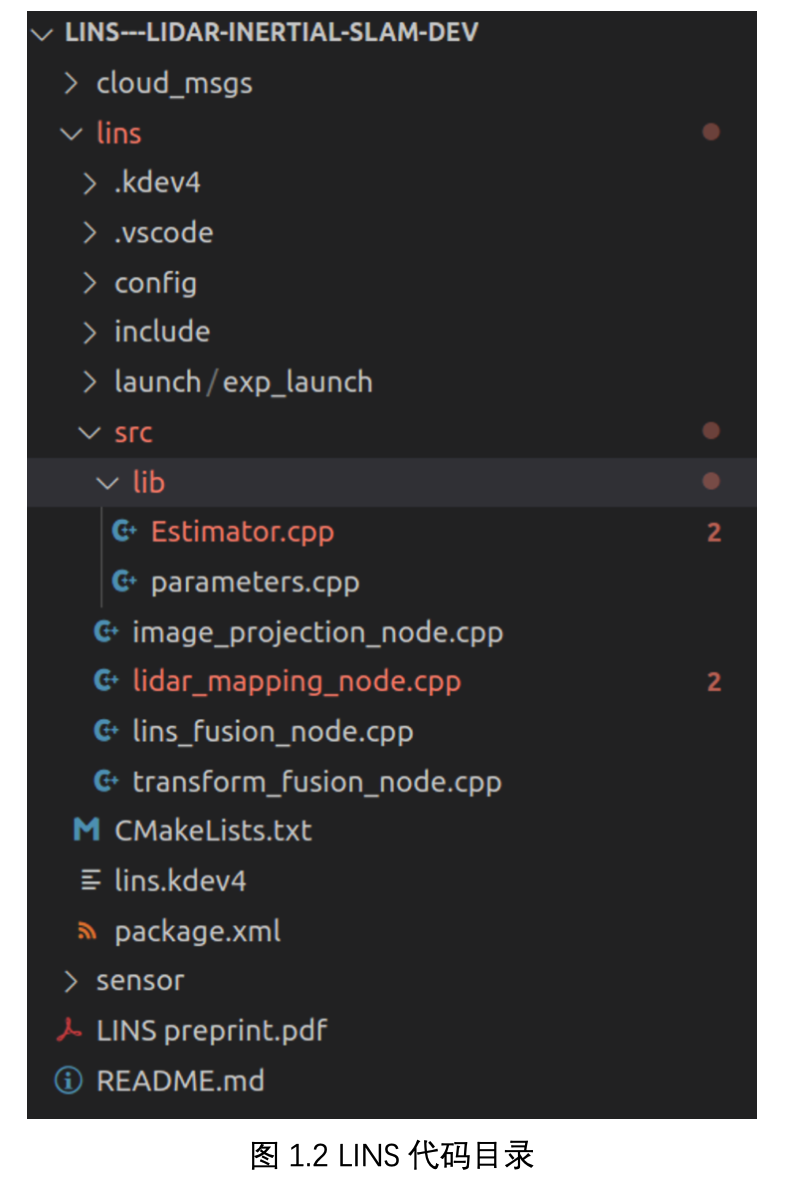
理论与代码分析
(一)LINS 是如何将激光观测引入滤波框架的?1、从代码中可以看出,LINS只是前端里程计部分采用了滤波框架(即 scan-to-scan 估计帧间位姿),而后端 scan-to-map部分仍然采用优化方式求解(即用 LM 方法求解位姿)。2、将点线/点面距离残差作为观测方程引入到代价函数中。根据论文公式 12,可以看到代价函数分为两个部分,前面是最小化误差状态(即最小化后验与后先验状态之差),后面的复合函数 f(x)表示点线/面距离,即最小化点线/面距离。也就是说把点线/面距离残差作为观测方程,有了观测方程,然后带入卡尔曼滤波相关公式即可求解。不过,作为一个创新点,作者采用了 IESKF,即迭代误差卡尔曼作为滤波框架。
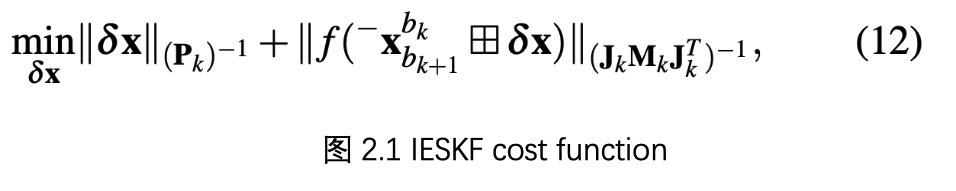
IESKF 与 ESKF 最大的区别就是,在做状态更新时是采用迭代求解的方式计算的,类似高斯牛顿等优化方法求解时需要多次迭代直到收敛。通过迭代的求解的方式,与 ESKF 相比可以得到更精确的解。对应论文公式 16。
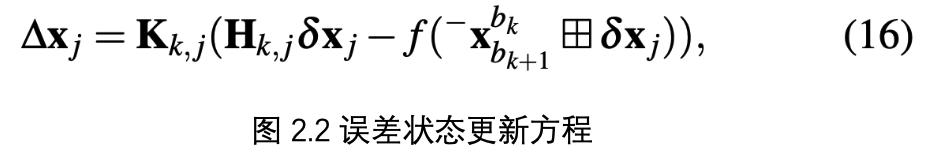
3、LINS 代码实现。LINS 中滤波相关的核心部分在 include/StateEstimator.hpp 中的 performIESKF()函数中实现。
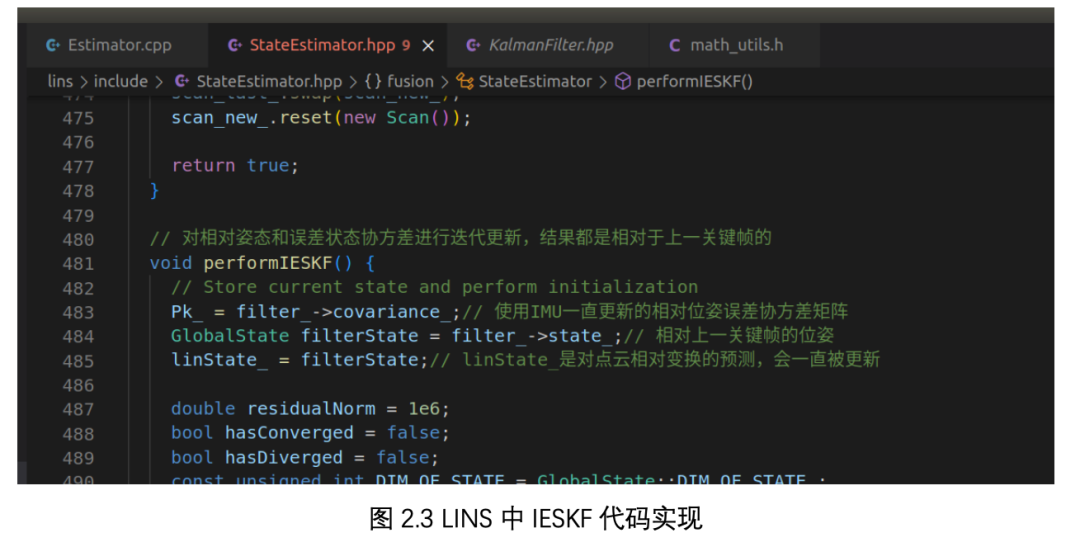
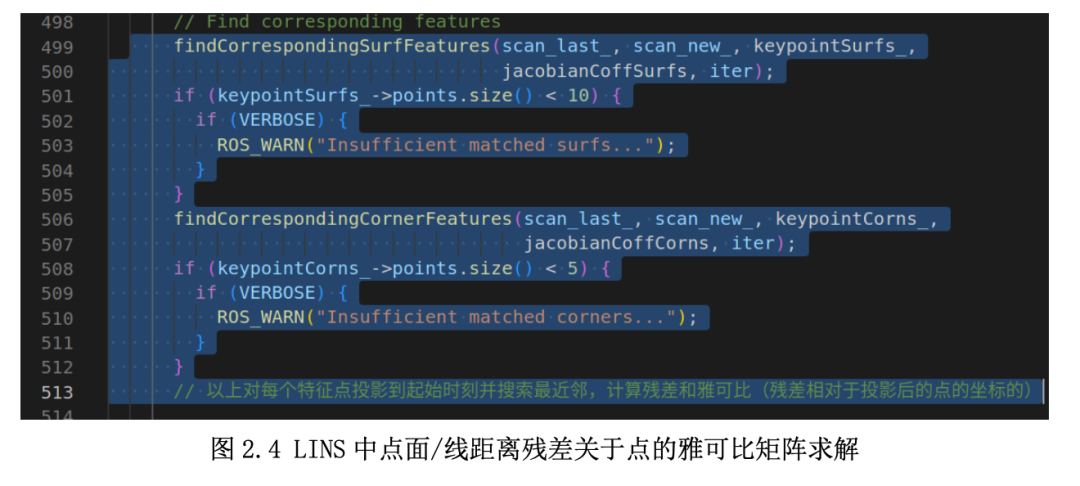
代码中基本是按照论文中的公式 12-18 实现的,比较好读懂。代码中的 findCorrespondingSurfFeatures(), findCorrespondingCornerFeatures() 函数即为 costfunction 中的点面/线距离残差计算函数,基本沿用了loam的实现方式,其中jacobianCoffSurfs, jacobianCoffCorns 变量为点面/线距离残差关于点的雅可比矩阵,该过程在之前推送的文章《泡泡点云时空 LOAM 专题-3】LOAM 代价函数设计与雅可比求解详细推导(上)》有详细的推导,感兴趣的可以去看下。
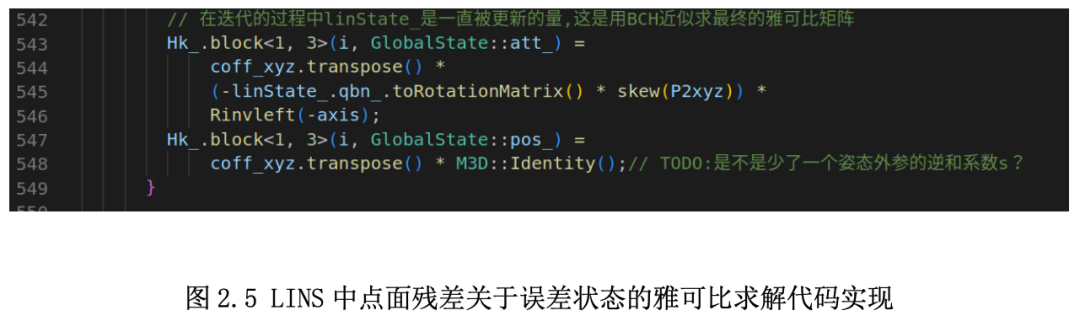
代码中,Hk_为点面/线距离残差关于误差状态的雅可比矩阵,作者是用 BCH 近似求解的,其实含义上与 LOAM 算法在 Odometry,Mapping 部分最终求解得到的是一样的,都是点面/线距离关于误差状态的雅可比矩阵,只不过求解方式表达形式不同,LOAM 中姿态是用欧拉角表示的,LINS 是四元数。
performIESKF()函数的剩余部分就是论文中公式 15-18 的实现,比较易懂就不赘述了。 (二)滤波与优化有何不同 其实,讨论滤波框架与优化框架的不同是一个相对比较大的问题,为了更具体一些,我们仅就 LINS 算法使用的 IESKF 做的滤波的 LIO 前端与 LIO-SAM 等以高斯牛顿或LM优化为框架的 LIO 前端做对比(当然严格意义上来说,LIO-SAM 的前端其实只有预积分,省略了激光里程计,使用 scan-to-map 匹配校正 imu 零偏,但是不影响我们的分析过程)。 1、框架差异。从框架上说,LINS 使用的 IESKF 是将所有的状态一起放到滤波框架里估计,而以 LIO-SAM 为代表的算法前端,是预积分+scan-to-map 算法,其中 scan-to-map 模块使用 LM方法计算帧图位姿,得到计算出的位姿后,输入预积分模块校正imu 零偏。也就是说 imu 零偏的估计与激光匹配位姿计算是分开的,而 LINS 使用了 IESKF 将二者当作状态一起估计。 2、理论差异。其实在 1993 年的论文[2]中就已经证明了 IKF 的更新方程与 Gauss-Newton 理论上是等价的。详细的推导过程可以参考论文,为了方便理解,我们在这里做一个简化的推导。 参照 LINS 论文中公式 15-17

当我们使用 Gauss-Newton 求解待估状态时,通常用到的公式是:
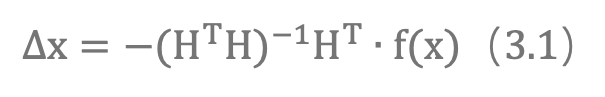
其实从方程的形式上,怎么看这个方程也与 LINS 中的公式 16 差别挺大。下面我们尝试尽量直白的解释下 Gauss-Newton 与 IESKF 更新方程的等价性。 对于一些刚接触SLAM的同学来说,可能有一个疑问是Gauss-Newton 求解时很少用到协方差矩阵,但是卡尔曼的更新方程中的卡尔曼增益是需要计算协方差矩阵的,如何理解? 其实 Gauss-Newton 只是一个公式,当我们设计误差函数时带有协方差矩阵,那么 Gauss-Newton 求解过程中就会有协方差矩阵的计算,实际上论文[2]中也正是通过这种方式证明的等价性。由于我们实际在用 Gauss-Newton 求解时基本不考虑协方差矩阵(指点云匹配求解位姿时),为了更好的理解,我们假设噪声相关的矩阵都为单位矩阵,那么 LINS 论文中的公式 15 变为:
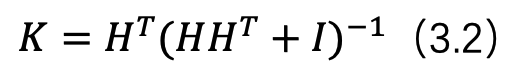
那么公式 16 变为
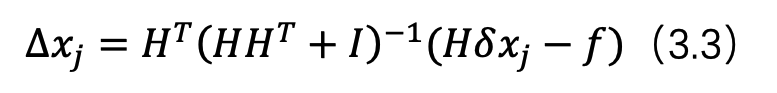
到这一步可以看到跟 Gauss-Newton 的方程不一致。这个时候要借助一个重要的公式实现转换,即 matrix inversion lemma,即矩阵求逆引理,即如果 A,C 为非奇异矩阵,那么有

那么公式 16 可以变为:
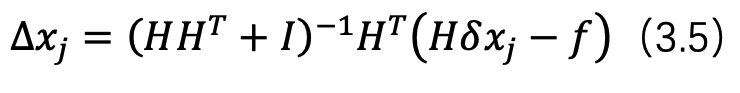
到这里,其实我们看这个形式跟优化的方法已经很像了,但是跟标准的高斯牛顿求解方程还是不一致。现在我们定义如下观测方程:
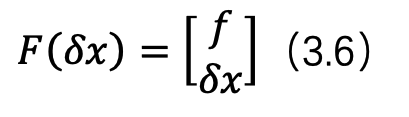
则其对应的雅可比矩阵为,
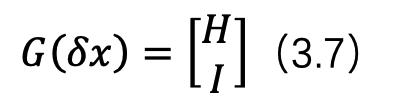
因此,
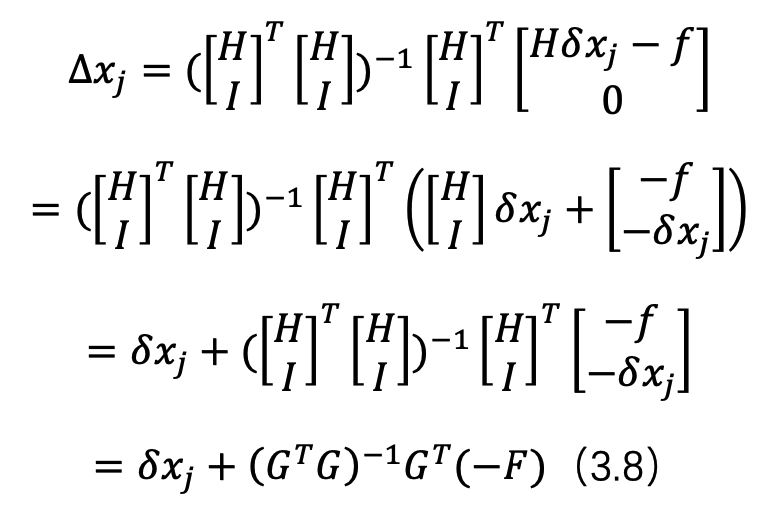
可以看到此时方程出现了我们熟悉的高斯牛顿的公式。因为滤波的框架里面其实是同时考虑状态方程与观测方程,因此使用最小二乘的框架构建的时候需要构建成如上形式。 个人的观点是,如果单从最终的公式来看,使用高斯牛顿求解两帧点云的相对位姿,与 LINS 中使用 IESKF 求解结果并不完全相等,因为求解出来的状态更新方程并不是完全一样,但是从理论上说,IESKF 的更新方程可以统一到最小二乘的框架里,因此效果上二者应该是近似的。
算法效果

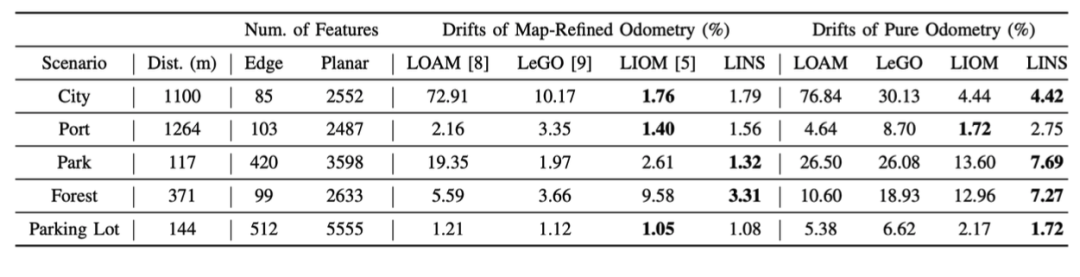
根据论文提供的实验结果,如果考虑前端+后端的整体处理效果,算法在公园与林间场景表现较好,但是在城区以及港口效果不及 LIOM。如果只考虑前端激光里程计,算法在除了港口场景外都是最优的,毕竟论文的主要贡献在前端。
总结
本文通过理论分析与代码对比介绍了 LINS 算法,其中主要介绍了 LINS 如何使用滤波框架做激光 SLAM,以及优化与滤波的区别。主要是把前端激光里程计部分改为了滤波框架,并且引入了 IMU 做紧耦合。同时,我们也推导了滤波的更新方程其实可以由高斯牛顿法推导而来。希望对读者有所帮助,如果错误烦请指出。
审核编辑:郭婷
-
激光雷达
+关注
关注
968文章
3971浏览量
189858
原文标题:LINS算法与代码解析
文章出处:【微信号:3D视觉工坊,微信公众号:3D视觉工坊】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
瑞芯微rv1126 SDK代码基础分析---rkmedia框架分析
基于元学习推荐的优化算法自动选择框架
基于等角紧框架的稀疏信号重构算法
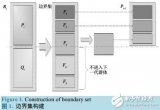
WIFI指纹定位算法的基本框架
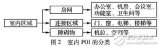
多项式插值算法框架
TouchGFX代码框架以及如何添加用户代码
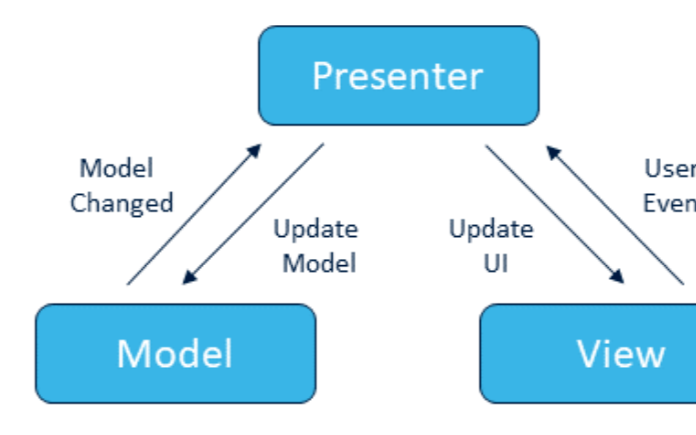
在单片机中使用的RTOS代码框架
大学课程 数据分析 实战之K-means算法(2)算法代码
AVM系统算法框架搭建的方法





 LINS算法的框架与代码分析
LINS算法的框架与代码分析










评论