摘要
我们提出了一个用于点云生成的概率模型,它可以被用于多种 3D 视觉任务的基础,例如形状补全、上采样、合成和数据增强。受非平衡热力学中扩散过程的启发,我们将点云中的点视为与热库(heat bath)接触的热力学系统中的粒子,其从原始分布扩散成为噪声分布。因此,点云生成相当于学习将噪声分布转换为所需形状分布的反向扩散过程。
具体来说,我们提出将点云的反向扩散过程建模为以某种隐式形状(shape latent)为条件的马尔可夫链。我们推导出训练时封闭形式的变分边界,并提供了模型的实现。实验结果表明,我们的模型在点云生成和自动编码方面取得了有竞争力的表现。
主要贡献
文章受非平衡热力学中的扩散过程启发,提出了一种新的点云概率生成模型。 • 作者从点云基于形状的条件似然的变分下限推导出一个易于处理的训练目标。
大量实验表明我们的模型实现了在点云生成和自动编码有竞争力的性能
方法概述
本文中作者将点云看作是从概率分布中取样生成的,每一个点都是该概率分布的独立同分布(i.i.d)采样。类似于图像的扩散概率模型,当我们向点云引入噪音时,点云会逐步从与形状有关的复杂分布变为高斯分布的噪音,这一过程被称作正向扩散过程。点云的生成模型可以被视作是如图二所示的逆向扩散过程:根据一个高斯分布取样作为噪音点云,训练一个神经网络以形状为条件逐步对该噪音点云减噪,直至点云恢复其本来的形状。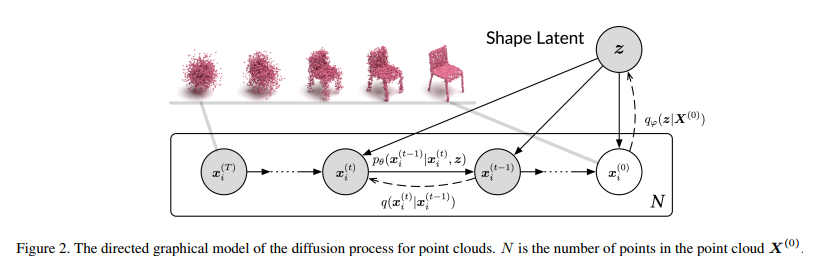
Figure 2 展示了从噪音点云逆扩散生成点云的过程可以由一个马尔科夫链模型表示。点云中的每一个点由 x(T) 开始以转移概率 p****θ(x(t-1)|x(t),z) 逐步减噪(逆扩散)为目标点云 x(0)。其中 θ 表示可学习的神经网络参数参数,z 表示与形状有关的潜变量。
生成点云时,从正态分布取样w,经先验flow模型映射为形状变量z。同时从正态分布取样噪音点云 x(T)。通过一系列逆向扩散过程,噪音点云以形状z为条件逐渐减噪为目标点云 x(0)。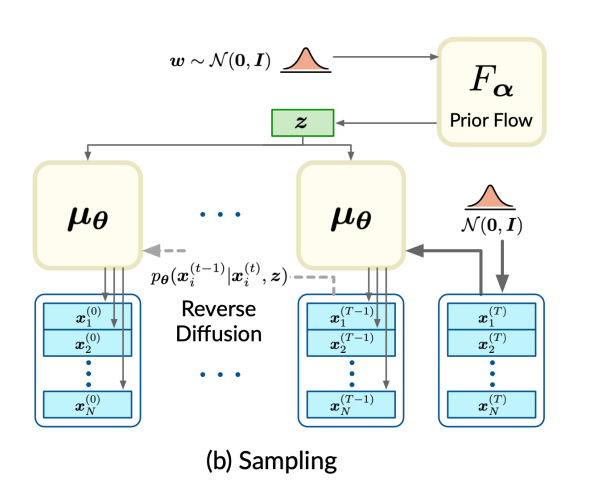
训练时,数据集中的点云经过编码器 φ 编码为形状潜码 z 正态分布的均值和方差,再使用与变分编码器(VAE)中的重新参数化技巧相同的方式取样形状潜码 z。如下图所示,输入点云随后经过一系列前向扩散过程逐渐变为噪音点云。训练目标函数采用条件似然概率的变分下限,以最大化似然训练数据集的似然概率。
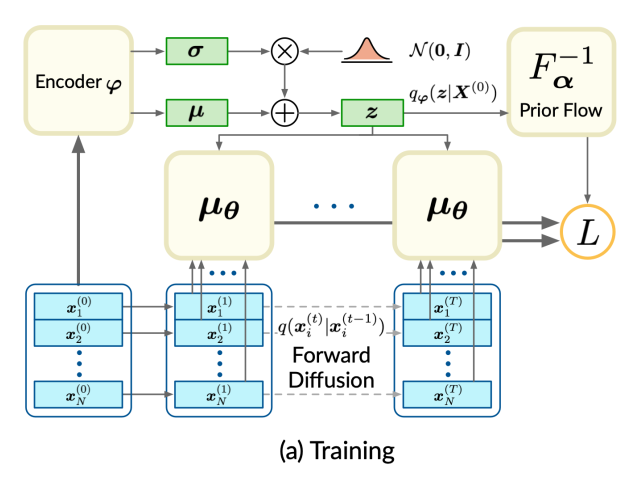
需要注意的是,变分自动编码器VAE的先验概率选用正态分布,本文应用 Flow 模型将简单的正态分布映射 p(w) 到更复杂的分布模型 p(z)。训练时,q(z|x(0) 经过逆向的 Flow 映射回 w, 损失函数包含 w 的先验概率分布和后验概率分布之间 KL 散度。
实验结果

文章选用 ShapeNet 数据集进行点云生成实验、点云重建以及点云特征提取实验。 Table 1 总结了扩散概率模型与包括GAN、Flow模型在内的其他点云生成方法相比在最小匹配距离 (MMD), 覆盖分数 (COV), 最近邻分类器准确率(1-NNA)以及 Jenson-Shannon 散度 (JSD) 上可以 SOTA 方法媲美。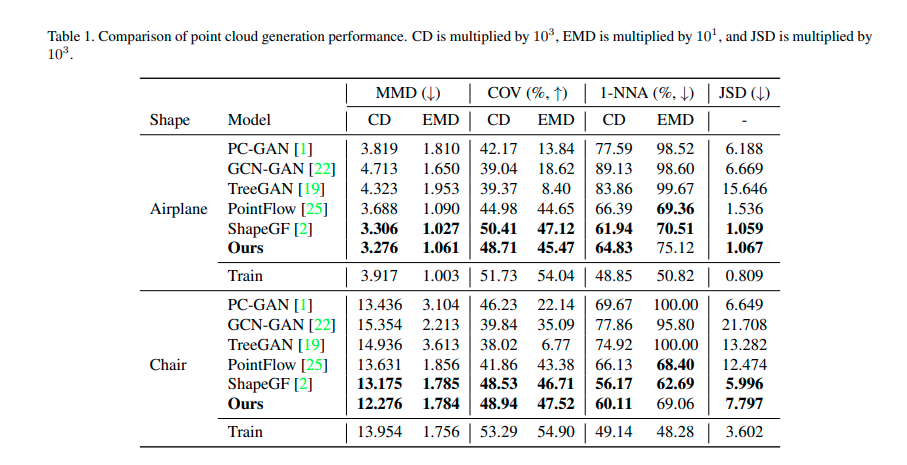
下图展示了一些生成点云的样例,包含了飞机和椅子两个分类。
Table 2 列出了扩散概率模型自动编码重建性能。其重建点云与原始点云之间的 Chamfer 距离(CD) 和 动土距离 (MD) 也可以达到与 SOTA 相近的数值。 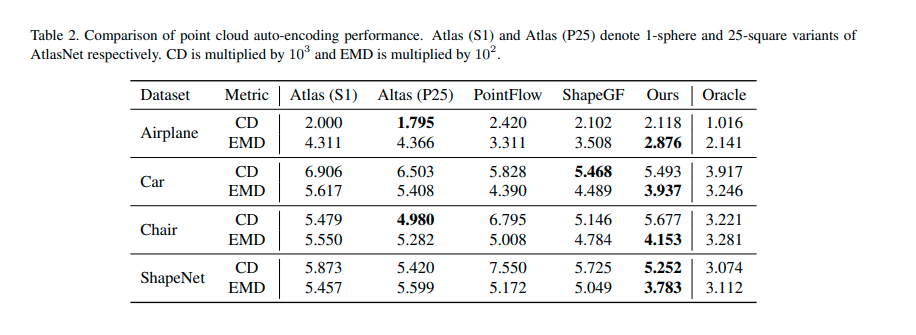
下图给出了几个点云重构的例子,最左侧一列是真实点云,然后依次是扩散模型、ShapeGF 以及 AtlasNet。
Table 3 显示扩散概率模型与其他模型在表征学习方面的比较。只使用一个线性SVM作为分类器,扩散概率模型学习的表征在ModelNet10和ModelNet40数据集上分别可以达到94.2%和87.6%的准确率,与SOTA方法相近或更好。 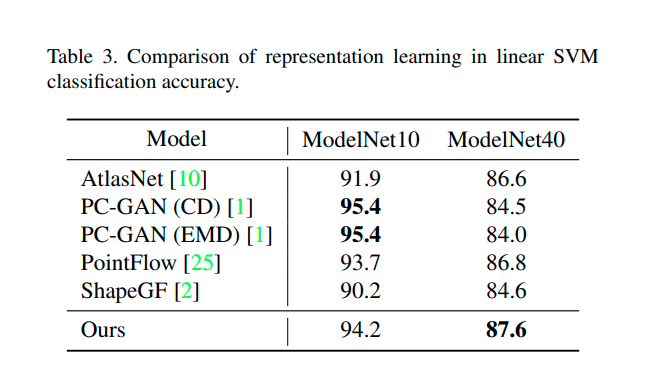
Figure 6展示在潜变量空间插值变换获得相应点云的变化:
总结
文章将扩散概率模型用于点云生成,推理时以形状采样为条件将噪音点云逆向扩散为目标点云;训练时将输入正向扩散为噪音点云,以从点云似然变分下限推导出的损失函数训练模型。• 实验表明这样的扩散模型实现了在点云生成、自动编码以及表征学习任务实现了有竞争力的性能。
审核编辑:刘清
-
编码器
+关注
关注
45文章
3640浏览量
134467 -
GaN
+关注
关注
19文章
1935浏览量
73372 -
MMD
+关注
关注
0文章
3浏览量
6691
原文标题:3D点云生成的扩散概率模型(CVPR 2021)
文章出处:【微信号:3D视觉工坊,微信公众号:3D视觉工坊】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
NVIDIA推出全新生成式AI模型Fugatto
阿里云开源Qwen2.5-Coder代码模型系列
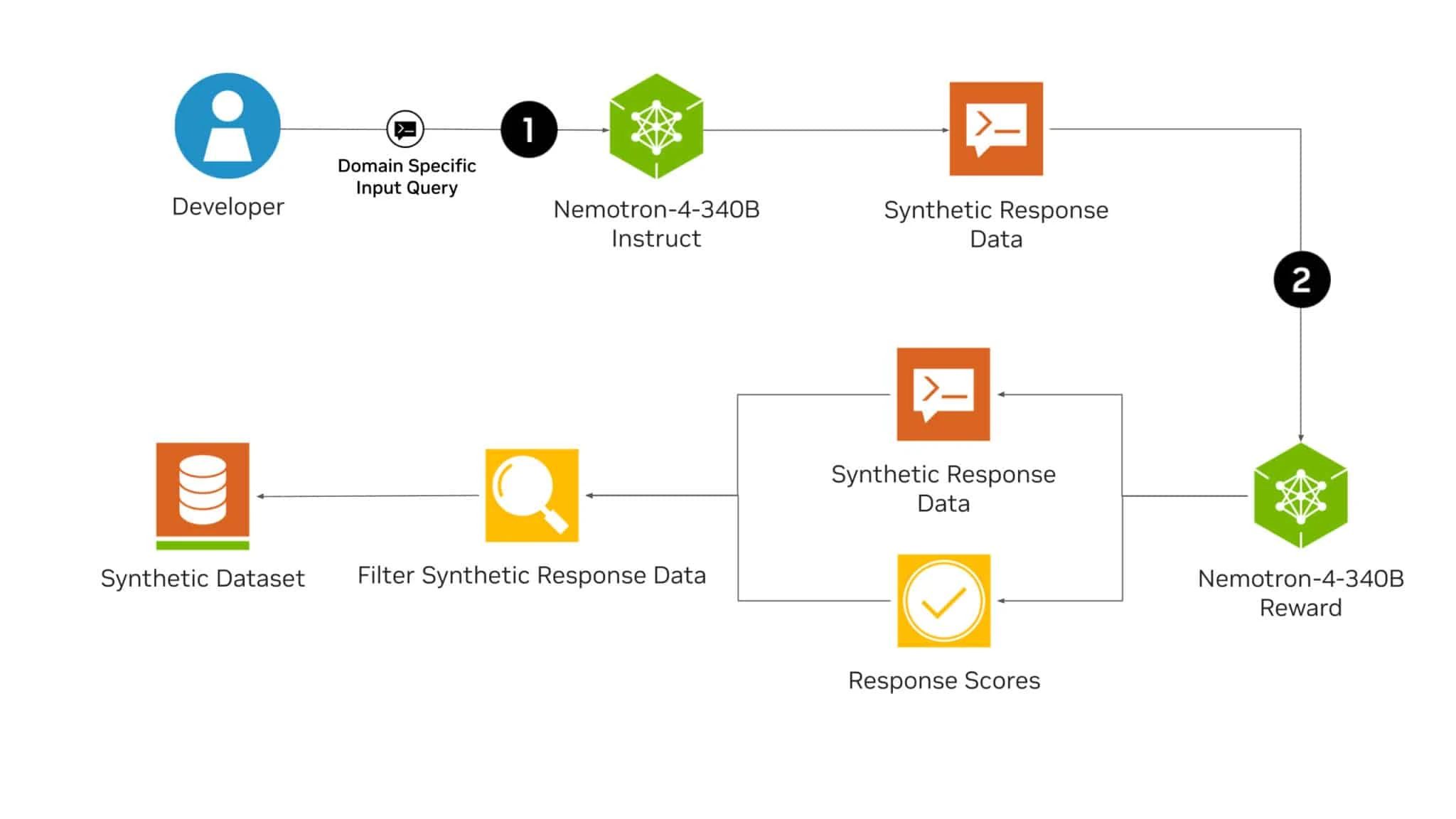
NVIDIA Nemotron-4 340B模型帮助开发者生成合成训练数据
北京灵奥科技基于亚马逊云科技打造大模型中间件
AD8275 spice模型“AD8275.cir”自动生成了一个LTspice模型用来仿真,仿真时弹出图片所示窗口如何处理?
基于stm32h743IIK在cubeai上部署keras模型,模型输出结果都是同一组概率数组,为什么?
ISEDA首发!大语言模型生成的代码到底好不好使





 介绍一个用于点云生成的概率模型
介绍一个用于点云生成的概率模型











评论