如何使用傅立叶分析各种非正弦波形中谐波分量的幅度及相位关系

所有的重复波形都可以由许多正弦波的组合组成。可以分析任何波形以确定分量数量。在本文中，学习如何使用傅立叶分析来确定各种周期性非正弦波形中谐波分量的幅度及其与基波分量的相位关系。

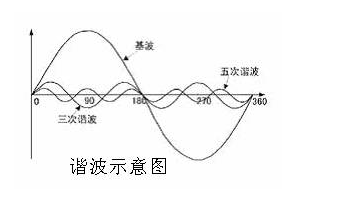
谐波是基频的整数（整数）倍（第二、第三、第四等）的频率。配电线路的基频为 60 Hz，每秒从正到负 60 个周期变化。例如，60 Hz 配电线路上的二次谐波为 120 （60 × 2） Hz。二次谐波在同一时间段内在基波的一个周期中完成两个周期。

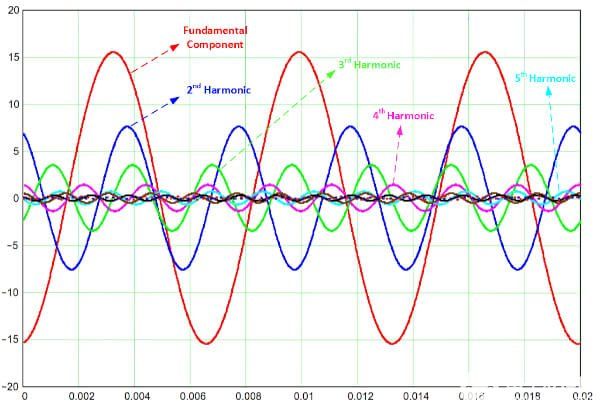
图 1.谐波是基频的整数倍（第二、第三、第四、第五等）的频率。图片由 Amna Ahmad 提供

傅里叶分析（由数学家 Jean Fourier 开发）是一种数学运算，可分析波形以确定其谐波含量。可以确定每个谐波的幅度，以及它与基波的相位关系。此外，可以计算任何直流分量的电平。

方波

纯方波，在地平面上下对称 ［图 2］，可以通过傅里叶分析显示，由以下等式表示：

e=4Emπ［sinωt+sin3ωt3+sin5ωt5+ fracsin7ωt7+.。。］（1）e=4Emπ［sinωt+sin3ωt3+sin5ωt5+ fracsin7ωt7+.。。］（1）在哪里

e是时间 t 的瞬时值

4Emπ4Emπ 是波形的峰值

sinωt 是一个基本分量

sin3ωt3sin3ωt3 是三次谐波

sin5ωt5sin5ωt5 是五次谐波

s一世n7哦吨7sin7ωt7 是七次谐波

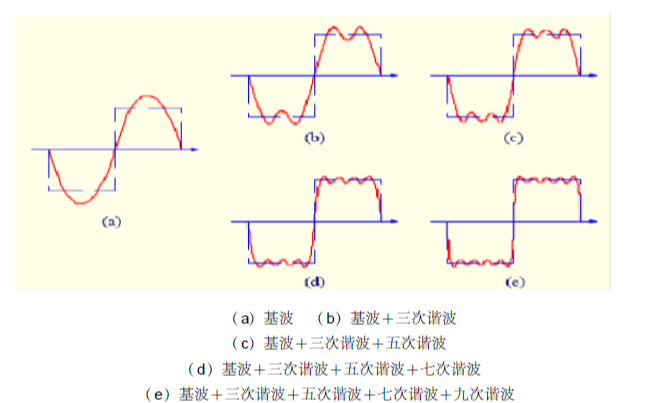
如方程所示，对称方波可以由基波分量和奇次谐波组成，但没有偶次谐波和直流分量。

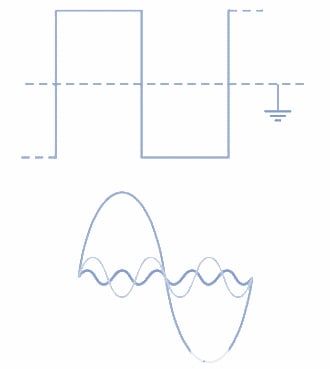
图 2.对称方波的谐波分析表明它包含基波和奇次谐波。图片由 Amna Ahmad 提供

注：傅里叶分析可应用于所有重复波形以确定其谐波含量。

锯齿波

图 3 中锯齿波的傅立叶方程为

和=2和米圆周率［s一世n哦吨−s一世n2哦吨2+s一世n3哦吨3−s一世n4哦吨4+s一世n5哦吨5.。。］（2）e=2Emπ［sinωt−sin2ωt2+sin3ωt3−sin4ωt4+sin5ωt5.。。］（2）在这种情况下，所有谐波都存在，同样没有直流分量。一般来说，当波形在地平面上下对称时，它没有直流分量。

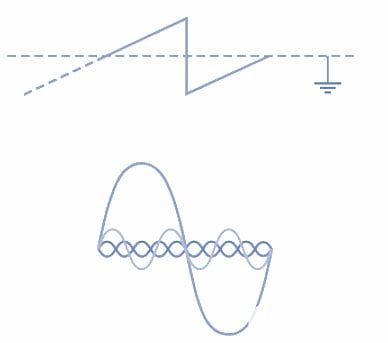
图 3.对称锯齿波的谐波分析表明它由基波和所有谐波组成。图片由 Amna Ahmad 提供

整流波

图 4 中的全波整流正弦波可以表示为

和=4和米圆周率［12+C○s2哦吨3−C○s4哦吨15+C○s6哦吨35.。。］（3）e=4Emπ［12+cos2ωt3−cos4ωt15+cos6ωt35.。。］（3）

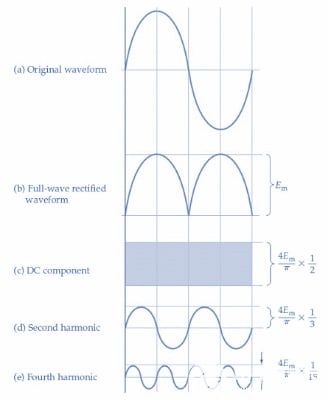
图 4.全波整流正弦波包含直流分量和偶次谐波，其幅度随着谐波次数的增加而减小。图片由 Amna Ahmad 提供

等式 3 显示波形具有直流分量 \（\frac{4E_{m}}{2\pi}\） 和偶次谐波 2ωt、4ωt、6ωt 等（图 4）。看起来没有基频分量。但是，在这种情况下，基频被取作整流前波形的输入频率 （f）。可以说，整流波形的基频实际上是 2f。例如，一个 60 Hz 的正弦波在经过全波整流后，会产生一系列频率为 120 Hz 的正弦半周期。4和米2圆周率4Em2π 和偶次谐波、2ωt、4ωt、6ωt 等（图 4）。看起来没有基频分量。但是，在这种情况下，基频被取作整流前波形的输入频率 （f）。可以说，整流波形的基频实际上是 2f。例如，一个 60 Hz 的正弦波在经过全波整流后，会产生一系列频率为 120 Hz 的正弦半周期。

谐波幅度

检查方波、锯齿波和整流正弦波的方程表明，在所有情况下，谐波分量的幅度都随着谐波频率的增加而减小。因此，高次谐波的重要性似乎越来越低。就这些分量对波形的 rms 值和负载消耗的功率的贡献而言，这当然是正确的。然而，为了良好地再现波形，必须存在许多高次谐波。例如，在方波的情况下，可能需要高达 11 次谐波（或更高）的所有分量。对于脉冲波形，可能必须存在高达百分之一的谐波才能产生良好的输出波形。

方波示例

具有 2 V 峰峰值幅度的方波在地平面上下对称。计算直到七次谐波的每个分量的幅度。

解决方案。

根据等式（1），

和=4和米圆周率［s一世n哦吨+s一世n3哦吨3+s一世n5哦吨5+s一世n7哦吨7+.。。］e=4Emπ［sinωt+sin3ωt3+sin5ωt5+sin7ωt7+.。。］E m = 1 V（峰值）

4和米圆周率=4×1圆周率=1.27在4Emπ=4×1π=1.27V基本\（E_{m1}=\frac{4E_{m}}{\pi}=1.27V\）和米1=4和米圆周率=1.27在Em1=4Emπ=1.27V三次谐波\（E_{m3}=\frac{4E_{m}}{3\pi}=0.42V\）和米3=4和米3圆周率=0.42在Em3=4Em3π=0.42V五次谐波\（E_{m5}=\frac{4E_{m}}{5\pi}=0.52V\）和米5=4和米5圆周率=0.52在Em5=4Em5π=0.52V七次谐波\（E_{m7}=\frac{4E_{m}}{7\pi}=0.18V\）和米7=4和米7圆周率=0.18在Em7=4Em7π=0.18V请注意，计算出的谐波电压分量都是峰值。每个都必须乘以 0.707 以确定 rms 值。

整流正弦波示例

全波整流正弦波的峰值幅度为 30 V，（预整流）频率为 60 Hz。计算直流分量和直到六次谐波的谐波分量的 rms 值。此外，确定谐波频率。

解决方案。

根据等式（3），

和=4和米圆周率［12+C○s2哦吨3−C○s4哦吨15+C○s6哦吨35.。。］e=4Emπ［12+cos2ωt3−cos4ωt15+cos6ωt35.。。］4和米圆周率=4×30圆周率=38.2在4Emπ=4×30π=38.2V直流分量\（E_{dc}=\frac{4E_{m}}{\pi\times2}=19.1V\）和dC=4和米圆周率×2=19.1在Edc=4Emπ×2=19.1V基本\（E_{m1}=0\）和米1=0Em1=0二次谐波 \（E_{m2}=\frac{4E_{m}}{3\pi}=12.7V\） \（E_{2}=0.707\times E_{m2}=9V\） \（f_{2 }=2f_{1}=2\times60=120 Hz\）和米2=4和米3圆周率=12.7在Em2=4Em3π=12.7V

和2=0.707×和米2=9在E2=0.707×Em2=9V

F2=2F1=2×60=120H和f2=2f1=2×60=120Hz四次谐波 \（E_{m4}=\frac{4E_{m}}{15\pi}=2.5V\） \（E_{4}=0.707\times E_{m4}=1.8V\） \（f_{ 4}=4f_{1}=4\times60=240Hz\）和米4=4和米15圆周率=2.5在Em4=4Em15π=2.5V

和4=0.707×和米4=1.8在E4=0.707×Em4=1.8V

F4=4F1=4×60=240H和f4=4f1=4×60=240Hz六次谐波 \（E_{m6}=\frac{4E_{m}}{35\pi}=1.1V\） \（E_{6}=0.707\times E_{m6}=0.78V\） \（f_{ 6}=6f_{1}=6\times60=360Hz\）和米6=4和米35圆周率=1.1在Em6=4Em35π=1.1V

和6=0.707×和米6=0.78在E6=0.707×Em6=0.78V

F6=6F1=6×60=360H和f6=6f1=6×60=360Hz

结论

通过谐波分析，周期性非正弦波形可以显示为由纯正弦波的组合组成，有时还带有直流分量。一个主要成分是与被分析的周期波具有相同频率的大幅度正弦波，它是基波。其他分量是正弦波，其频率恰好是基频的倍数。这些波，表示为谐波，根据它们的频率与基波频率的比率进行编号。