1 前言
在很多实际工程问题当中,非线性系统占大多数,而卡尔曼提出来的卡尔曼滤波器是一种针对线性系统的估计算法[1]。 为了解决这一问题,Schmidt学者分析了卡尔曼滤波器中的系统模型部分,并提出将卡尔曼理论应用到非线性系统的扩展卡尔曼算法 Extended Kalman Filter(EKF)[2]。相比于线性卡尔曼滤波器,扩展卡尔曼滤波器有更广的适用范围[3, 4],更高的状态估计精度,可以处理任意更新频率的系统。 有了上文的基础,这里,我们将通过一个二维小车的例子并来介绍扩展卡尔曼滤波的原理。
2 扩展卡尔曼滤波算法介绍
在介绍扩展卡尔曼滤波算法之前,我们先回忆一下之前介绍的卡尔曼滤波算法:
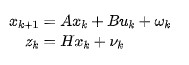
其中前两个公式为系统状态预测部分,后三个公式为系统的修正部分。其中整个系统最重要的是要通过公式将系统的模型和测量与状态之间的关系表示出来:
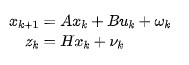
式中为系统矩阵,为控制矩阵,为观测矩阵。为目标在时刻的状态,为控制量,和分别为系统误差和测量误差。在线性卡尔曼滤波算法中,和是常值矩阵,其对应的系统就是线性系统。如果想将卡尔曼理论应用到非线性系统中,则需要对非线性系统进行线性化处理。
2.1 扩展卡尔曼滤波算法的不同
非线性系统方程及其观测方程通常可以表示为:
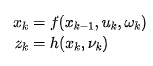
扩展卡尔曼滤波算法可以通过将非线性系统在其参考点处做泰勒级数展开,从而使非线性系统可以线性化。展开后,我们可以得到:
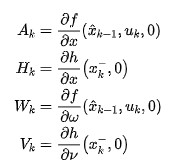
其中和是非线性系统函数在时刻求偏导数后的雅可比矩阵,和为非线性测量函数求偏导数后的雅克比矩阵。那么,扩展卡尔曼滤波算法可以写成:
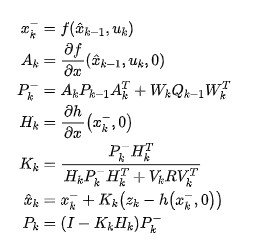
介绍完公式,接下来我们将通过2维平面内的小车来对扩展卡尔曼滤波算法进行讲解。
3 二维小车实例
如果要估计一个在二维平面内运动的小车,首先要根据要求选择一个较为合适的系统模型。在二维平面内,小车的运动可能是直线也可能是曲线,那么在一维平面用的线性匀速模型constant velocity model(CV) 将不适用。这里将采用一个简单的非线性模型匀转速、速度模型 constant turning rate and velocity magnitude model(CTRV)。
3.1 非线性模型CTRV
ctrv模型是cv模型的一般形式。这里我们假设观测到的状态变量为:
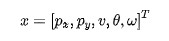
分别对应目标在,方向上的位置,速度,角度和角速度,变量之间的关系如图1所示。
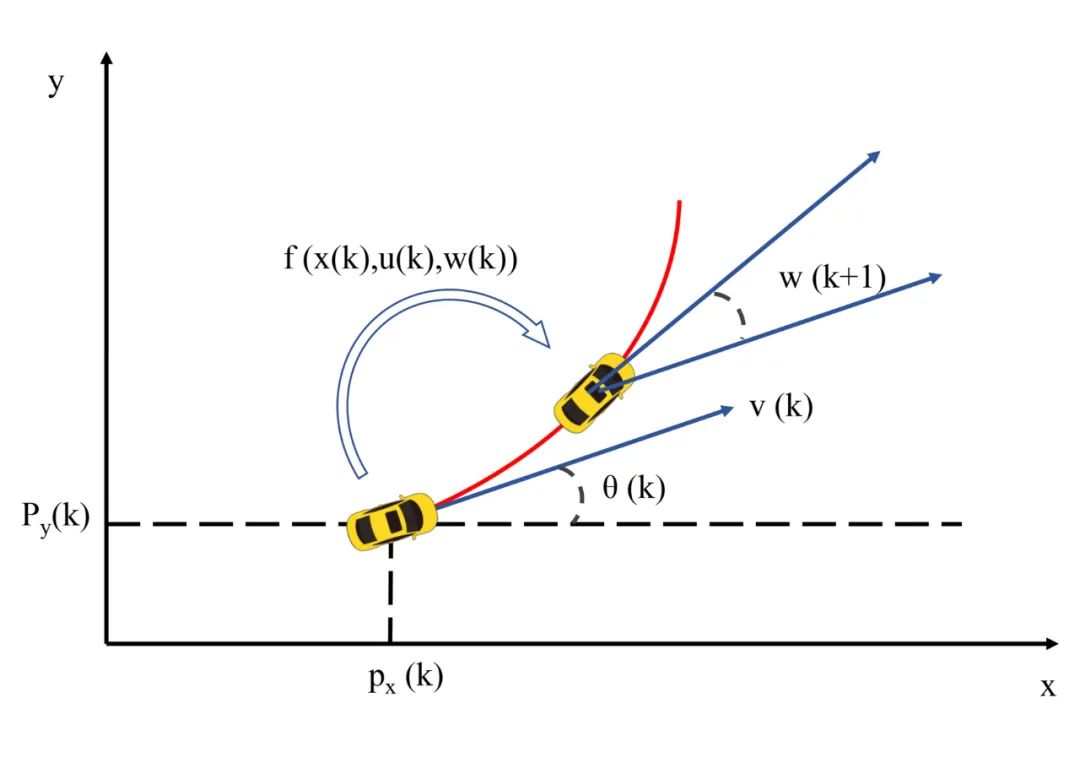
图 1: 二维平面ctrv模型
状态量关系从图中可以看出,各变量之间的相互关系。那么,从时刻到时刻,状态的变化应该是:
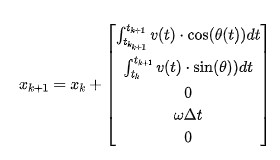
根据积分,我们可以得到下式:
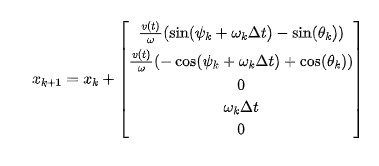
这里,我们对系统函数求偏导得到其雅克比矩阵为
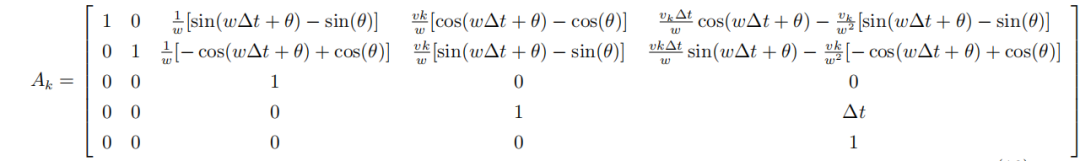
这里为了将系统误差为:
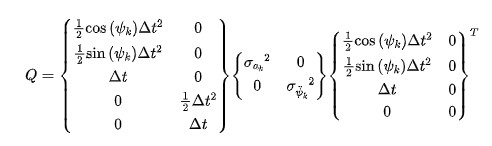
后续再套入到卡尔曼滤波器中,我们就可以得到一个CTRV的跟踪模型:
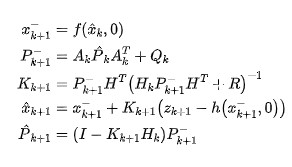
3.2 仿真
这里我们假设二维小车系统可以观测到目标的位置:
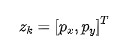
那么观测方程为:
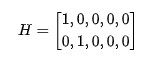
仿真总时间10s,时间间隔,目标小车绕原点,半径以速度做匀速圆周运动。观测信息为目标的位置,测量误差。
从视频中我们可以看到,不同的模型即使在当前估计状态相差不大的情况下,其估计目标未来的状态也是有很大差别的。在这个例子中,目标做的是匀速绕圈运动,CTRV模型更能描述系统的运动状态,但该模型是非线性系统。因此,需要结合EKF,来实现对非线性系统的状态跟踪和预测。
仿真结果如图2所示,红色轨迹为小车真实轨迹,红点为测量小车位置,蓝色圆圈为CV模型估计的小车当前位置,绿色圆圈为CTRV模型估计的小车当前位置,蓝色实线为CTRV模型估计小车轨迹,蓝色虚线为CTRV模型预测未来一段时间内的小车轨迹,绿色实线为CV模型估计小车轨迹,绿色虚线为CV模型预测未来一段时间内的小车轨迹。可以看出CTRV模型的预测比CV模型的预测在绕圈运动中更为准确。
4 总结
在很多实际工程问题中,系统的描述总存在不同程度的非线性,如平方、三角函数等。针对这一问题,EKF的思路是将非线性系统线性化转换为近似的线性系统,然后应用卡尔曼滤波算法完成状态估计。
审核编辑:汤梓红
-
滤波器
+关注
关注
161文章
7799浏览量
178011 -
滤波算法
+关注
关注
2文章
88浏览量
13718 -
卡尔曼滤波器
+关注
关注
0文章
54浏览量
12185
原文标题:扩展卡尔曼滤波器介绍
文章出处:【微信号:雨飞工作室,微信公众号:雨飞工作室】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐

基于DSP的扩展卡尔曼滤波直流无刷电机控制
自由转子陀螺的漂移误差模型识别系统
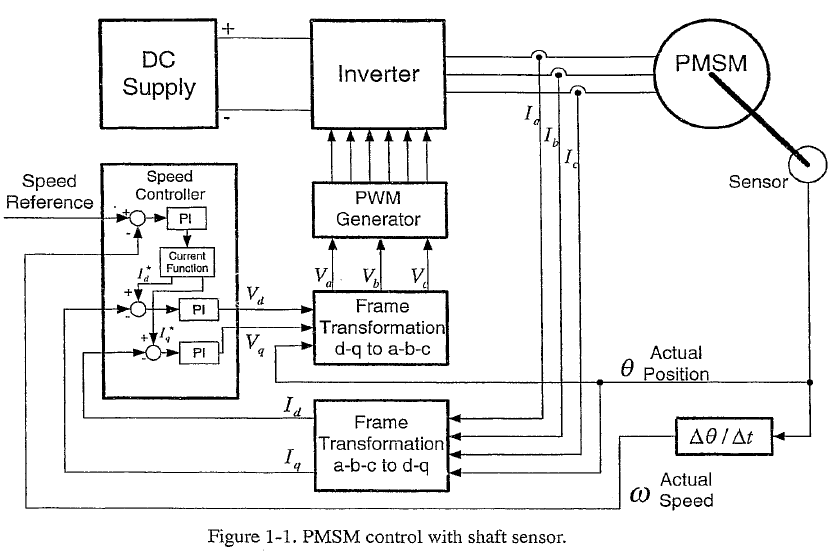
扩展卡尔曼滤波在永磁同步电机无位置传感器控制中的应用详细概述
基于扩展卡尔曼滤波等的齿轮啮合刚度辨识算法
基于扩展卡尔曼滤波的机动目标航迹跟踪
基于扩展卡尔曼滤波EKF的无感控制+Matlab/Simulink仿真案例
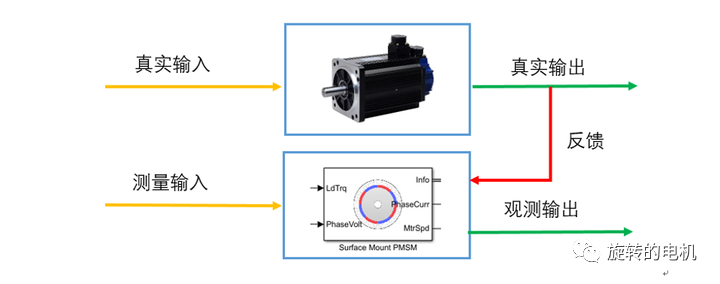




 扩展卡尔曼滤波的原理
扩展卡尔曼滤波的原理

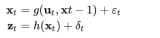










评论