可能有人感觉这个标题有点小题大作,温度,不就是对物体冷热程度的描述吗?负温度,不就是零下多少度嘛!
真的这么简单吗?当然不是!
“描述物体冷热程度”的说法。只给出一种模糊的定性解释,与“质量是什么?”的常见答案——“质量是指物体所含物质的多少”一样,并不能真正的回答问题。而负温度与零下温度则完全是两回事。
其实,这个问题与诸如“时间是什么?”、“质量是什么?”一样,都是非常深奥的大问题。历史上,人们对温度的认识,经历了漫长的过程。
但要讲清楚温度的含义,只讲温度本身是不可能的,必然涉及热学中很多相关知识,例如热力学第零定律,温标,热的本质,热力学第二定律,卡诺定理和负温度等等。因此,本文就以温度为主线,来聊聊热学背后的逻辑结构和各部分的关系。
01
冷热的体验
由于天生具有对冷热的感受,人类需要一个词语以描述物体的冷热程度,于是温度一词就提出了,但那时候,温度不过是一种定性的描述:热指温度高,冷指温度低。
凛冬之日,你来到院子里,面对石凳和木椅,你一般会选择后者坐下,因为经验告诉你,它相对没那么冰冷。也就是说,石凳的温度比木椅要低一些?
秋高气爽,习惯吹空调的你,从屋内迈出时,迎面而来是一阵炙烤般的热浪,而当你从树荫下走出时,你却又感觉阳光如此温和。抬头看,天还是那个蓝天,太阳还是那颗太阳。
学过中学物理的人知道,上面例子中的冷热的不同体验并非由不同的温度导致,而分别是由导热性能的差异以及前后温差对比造成的。倘若不信,可用温度计测量木椅和石凳的温度,你会得到相同的结果。
由此可见,温度并非总是与我们的主观感受一致——废话,科学概念焉能为主观所左右!那么温度到底是什么呢?你可能会说,温度不就是某种温度计的度数吗?当然是这样,但真正理解温度计的度数,你得先理解温度这个物理量。
那么,作为一个物理量,温度是如何被定义的呢?
想想,一个物理量从无到有,应该怎么被科学的定义呢?下面以以质量为例,看看物理量应该如何被确立。
02
以质量为例
中学物理中讲:质量是指物体所含物质的多少。但实际上,这句话等于什么也没说。考虑一块均匀的铁,你把它切成多块,如果你认为,体积大的物质多,这当然没问题。
但问题是,你怎么比较不均匀的铁块呢?进一步的,你怎么比较组份不同的物质的多少呢?(注意,不要想着去比较摩尔数,那可是另外一个物理量哦!)是的,你没有办法!可见,这种定义方法依赖物质的种类,没有普适性。
后来,人们通过牛顿第一运动定律认识到,惯性是任何物体必然具有的一种属性。人们进一步发现:质量就是这种属性的量度,质量不再与具体的物质成分有关,而是一种普适的量。
而进一步的研究表明,质量反映了合外力的作用下,物体获得加速度的难易程度,这就是质量的确切定义。该定义解决了质量这个物理量是什么的问题(当然不是指质量的本质来源),保证质量将可用数字来记录。从数学的角度讲,这保证了质量与力以及加速度之间存在某种函数关系,即
接下来,还要解决质量的标度问题(与此对应的,质量的定义是量度问题)。
根据牛顿第二定律,物体的加速度与合外力成正比,也就是说,上述函数关系可以化为力与加速度之比的函数,即很显然,满足上式的质量标度可以有多种选择。显然,直接选择质量等于合外力与加速度的比值是最简单的。这确立了质量标度,即
顺便说一下,牛顿在他的《自然哲学的数学原理》中就是按上述逻辑来定义质量的。关于质量是什么,他写道:“物质的数量(质量)是物质的度量并等于密度同体积的乘积”。而对于密度,他又写道:“我所说的物体有相同密度是指它们的惯性与它们的体积成正比”。
你可能会说,质量不是比力更基本吗?如果质量还要用力来标度,那不是乱套了?
其实,为一个物理量建立的标度,是为物理量的值找到一种普适的、与物质性质无关的函数关系,避免让它落入“经验”的陷阱,所以更多的是为理论上的统一。至于它的实际可操作性,并不苛求。关于这一点,温度的绝对温标就是如此,因为热的测量也是要依赖于温度。
当然,对质量而言,在实际操作上,我们总可以避开这个问题。
例如,根据胡克定律,让一根弹簧产生同样的力,以这个力去加速质量不同的物体和,二者加速度分别为和,则有或者,根据动量守恒定律,让两个物体发生弹性碰撞,如下图所示
设以初速度撞击静止的,二者末速度分别为和,则有上面比例式右边是简单可测的基本物理量,这样一来,循环定义的问题就解决了!
剩下的,我们只需要确定一个基准质量,也就是质量单位的参考数值——上面算式中的,那么其他的物体的质量——上面算式中的,就都可以按此比例关系来确定了。
一开始,人们以4摄氏度下1立方米的水的质量作为1000千克,后来又制作了直径与高度均为39毫米的铂铱合金圆柱体作为1千克的标准。现在一般用同位素的质量的1/12作为基本质量单元。
这样,质量这个物理量就算是完全建立了。
再后来,人们发现,质量还可以从引力的角度去定义,并且还借助普朗克常数重新定义了质量的标准,其标度与上述标度保持一致。
上述质量的定义是明确的,其标度与具体的物质无关,是普适的。
根据这个例子可知,定义一个物理量有如下两步:第一步,解决它是什么的问题,具体工作是:确认一定存在一个函数描述它;第二步,建立它的标度,具体工作是把那个函数给定下来,并且选择一个基准值。
自然的,温度也不例外,我们也应该先明确它是什么,然后再给出一个普适的标度。下面来看看这是怎么做到的。
03
热平衡的概念
在漫长的生活实践中,人们发现,冷热不同的物体相互接触,热的物体会变冷一点,而冷的物体会变热一点,经历足够长的时间之后,它们便具有相同的冷热程度,并且,人们发现,若使之与外界隔绝,这种共同的状态将一直维持不变,这种状态称之为热平衡态。
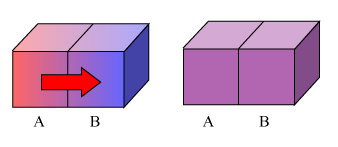
处于热平衡态的体系具有相同的冷热程度,也就是温度。换句话说,温度是所有处于热平衡的物体共同拥有的一种属性,它是热平衡的标志。
很显然,处于热平衡的物体之间应该不再有能量转移了,否则就不是热平衡,这就好像处于静电平衡的导体内没有电荷的定向移动一样。因此,两个温度相同的物体即使互相接触,也不会有热传递发生。而刚开始接触时,之所以有热传递,也是因为二者之间存在温度差。
相比之前关于温度的定义——物体冷热程度,通过热平衡的概念,温度的概念有了一种新的说法——热平衡的标志。该定义有什么进步之处?
冷热程度很多时候实际上是一种主观感受,并且实质上与热传导的快慢有关——由傅里叶的传热理论决定。所以,将温度定义为热平衡的标志,能避免把温度与热混为一谈的问题。
好了,现在对我们来说,温度不再只表示物体冷热程度,它还是热平衡态的标志——一种特有的属性。然而,这个神秘的属性仿佛藏得很深——它的确就在那里,我们还给它取名叫温度,可它究竟是什么呢?
能否将它表示为实数呢?换句话说,温度是否能表示为系统其他的参量的函数呢?注意这里只是讨论能不能,并没有要求是什么样的函数!
要保证上述问题的肯定答案,必须有一条假设来开路,这就是热力学第零定律。
04
热力学第零定律
1939年,英国物理学家、剑桥大学教授福勒(亦译作否勒)给出一条假设:
如果两个系统各自同第三个系统处于热平衡, 则这两个系统也彼此处于热平衡。
这就是热力学第零定律。之所以称作第零定律,是因为提出这个假设时,热力学第一、第二定律早已建立多年。但作为剑桥数学物理的领航者、狄拉克的老师,福勒的假设被发现是热力学最基本的假设——没有之一,故只好取了一个独特的名称:Zeroth law of thermodynamics。
为什么有了这个定律,就能确认温度函数的存在呢?
这涉及物理背后的严密的数学逻辑,福勒不愧是数理大家,他从严密的数学角度分析认为,只有假设热平衡具有传递性,即上述引文中所说的那种性质,才可保证温度函数的存在。
学过集合与映射的人很容易理解这样一件事:如果一个集合的所有子集内的成员都等价,并且这些子集没有交集。则可给这些子集赋予任意的数作为标签,自然的就建立了等价集到实数的映射,这就是函数。
换句话说,如果能将多个热平衡态的系统的集合划分成不同的等价集,我们也可以对其打标签,然后建立等价类与这些标签之间的映射,如果认为标签就是温度,那么这个映射就是温度函数。
那么,热平衡态能被划分成等价集吗?这需要作为集合的元素——各个热平衡系统满足三个性质:自反性,对称性和传递性。我们不妨采用数学中集合论的语言来重新考察下热平衡态。
首先,任何系统A自身也是热平衡的,这说明热平衡态是自反的。
其次,如果A和B处于热平衡,那么显然B和A也是一样处于热平衡,这说明热平衡是对称的。
再次,根据福勒的热力学第零定律,若C与A处于热平衡,且C与B也处于热平衡,则A与B必定也处于热平衡,这说明热平衡之间是可传递的。
由此可见,热平衡的确能被定义成等价关系,温度相同(处于同一个热平衡态)的系统都属于一个等价集,不同温度(相互不满足热平衡)系统则不属于一个等价集。因此,任何处于同一个热平衡的热力学系统必定可用一个普适的函数描述,即温度函数
其中,,,是体系可能用到的参量。
我们看到,热力学第零定律保证了温度函数的存在。这也是当年福勒提出热力学第零定律的原因。
好了,作为温度的定义部分,温度的量度确立了,剩下就是它的标度问题。
05
一些误解
在进入温标部分讨论之前,先说说对热力学第零定律常见的理解的问题。
热力学第零定律也可如下表述:
若A和B都与处于某个确定的状态的C处于热平衡态,则A与B也必定处于热平衡态。
很多教材上的表述不够严谨,例如有的教材说:
若先让A与B分别与C接触达到热平衡,则当A和B也处于热平衡态。
前半句容易被误以为A和B与C达到两个不同的平衡态,如果是这样,那A和B不可能处于平衡态的,所以这么表述是不对的。
还有的书强调A和B彼此绝热,但同时与C达到热平衡,以此来保证所达到的是同一个平衡态,并且给出类似下面的示意图

首先,该表述中说“A和B彼此绝热”,但明明它们都与C之间是导热的,怎么能做到彼此绝热呢?正确的说法是:A和B彼此没有接触。
更重要的是,这种说法本身也是对本定律的误解。实际上,本定律所说的是彼此处于热平衡,并不一定是接触后才达到热平衡。只要A和B与C的同一状态达到热平衡,即使是不同时,A和B也是处于热平衡的。温度计就是按照这个原理工作的。
当然,上面这种情况的确可以作为检验热力学第零定律的一种方式,但是热力学第零定律并不局限于这种情况。
总之,热力学第零定律只是基于实验事实给出一个数学假设,即赋予热平衡以传递性,即:如果A和B都与C处于热平衡,则A和B也处于热平衡,仅此而已,并不是说A和B同时或先后接触C,然后与C达到热平衡。
06
经验温标
在17世纪时,虽然人们对于温度的理解还远远不够,但这并不影响人们从各种热效应得到各种经验性的温标。因为,不可能等什么都搞清楚了才肯去应用,必须勇于尝试新事物才会有机会探索背后的奥秘,这一点在科学的进程中非常普遍。
人们注意到,冷热变化会给物体带来影响,最常见的是热胀冷缩,电阻,电动势等,此外,对体积(压强)固定的气体来说,还会产生压强(体积)的变化。于是,人们通过这些热效应检测温度变化,并由此发明了温度计。历史上第一个温度计是伽利略设计的。
这是怎么做到的呢?
本来,根据前面讲的温度函数的概念,一个普适的温标应依赖于一个普适的函数,而不依赖于具体的物质,但在当时,找到这样一个普适的温标函数是不可能的。
既然找到普适的温度函数很麻烦,那对特定的物质的特定属性,是否能找到一个简化版的温度函数呢?人们就是顺着这个思路建立了各种经验温标。
要建立一种经验温标,需要确定三件事:测温物质、物质的属性和温度与属性值之间的函数关系——简化版温度函数。当然,最简单的温度函数是一次函数,即
这里面有两个待定常数和。既然温标本质上是由人为约定的实数,那么可将某两个特定的状态的温度先规定下来,然后在据此将这两个常数确定。
根据这种线性关系,瑞典天文学家摄耳修斯(Anders Celsius)提出了摄氏温标。他采用水银的体积作为测温属性,将水的冰点和沸点分别定为0度和100度,代入上式得到故得到这里面的和分别是测温物质的属性在分别与处于冰点和沸点的水达到热平衡时的取值。将这两个刻度之间等分为100份,每一份就是1度,用表示度。因此第个刻度处就是若在冰点以下和沸点以上也刻出间隔相同的刻度,则温度计的测温范围就扩充到更大的范围。
摄氏温标基于一次函数而建立,是最简单的经验温标,温标也可能是更复杂的函数,例如热电阻是温度的2次函数,热电动势则是温度的3次函数,可用以实现更复杂温标。
实现不同的温标,要选择不同的工作物质及属性。对摄氏温标来说,水银,定压气体的体积,定容气体的压强都是不错的选择。
不同的经验温标所得的温度不一致,故要选择其中一种温标作为基准,其他都需根据此温标进行矫正。
若有人拿了一个根据没有矫正的温标制作的温度计测温,那么他必须在他的测量记录上说明他的测温物质和属性,否则他的测量是无意义的。这是经验温标的局限性。造成这个问题的根本原因是,经验温标没有普适性。
因此,必须建立普适的温标!
07
探求温度函数
根据上述温度的定义,我们相信,达到热平衡的体系所有的状态参量与温度之间满足一个确定的函数关系,即
这个函数的参量与一样,都与体系经历的过程无关,只与体系当前的状态有关,故该函数又名态函数,它的值就是温度值。
这里面的状态参量所对应的隐函数其实也是各自的态函数,换句话说,上式可看作是由态函数组成的方程,是的,它就是描述热力学的状态方程。因此,确定了温度函数,就等于确定了状态方程。
但是,怎么确定这个函数呢?
答案是:从实验中获得!只要我们意义测量平衡态下各种可能的参量的值,然后通过数据分析,应该能找到这个函数关系。
这里面的状态参量一般有四类,除热学的之外,还有力学的,电磁的和化学的。显然,体系越复杂,上述函数关系就越复杂。例如,体系处在电磁场中,就需要考虑电磁参量。
那么,我们就考虑那种最简单的系统吧,某种特定气体,没有电磁场的作用,那参量数应该很少了!是的,只剩下摩尔数,体积和压强了。这种情况下,温度函数应该是OK!那就找来某种无毒、安全和廉价的纯净气体,放入体积可变的容器中,再配上测压仪器。咱们来仔细研究下:处于热平衡的气体,其参量是否具有某种特定的关系,且这个关系式的值总等于一个常数呢?
这正是17世纪英国的科学家,现代化学的开山祖师玻意耳(Robert Boyle)要干的事。
在他的著作《关于空气弹性及其物理力学的新实验》中,他明确地提出
在密闭容器中的定量气体,在恒温下,气体的压强和体积成反比关系。
这就是玻意耳定律。需要指出:在气体越稀薄,即所谓理想气体时,实验数据越接近此规律。
设有摩尔气体,压强、体积分别为,使之经历等温变化,根据玻意耳定律有设有1摩尔相同条件气体的体积为,根据阿伏伽德罗定律:
压强、温度和摩尔数相同的任何气体的体积相同
故有
则根据玻意耳定律,也为常数,故有好了!变化的参量真的构造出一个常数了!这正好满足温度的需要。因此,前面的温度函数现在可写成
按前面所讲,这里不同的函数法则对应不同的温标。本着极简主义者的偷懒哲学,人们就选择了线性关系作为的法则,即其中,为待定常数。
你可能会说,干嘛搞这么复杂呢?既然想偷懒,就直接取作不香吗?
的确可以这么做!实际上你可以给参数取任意值,取决于你懒的程度。但就在这时,有一个更懒的人提出了一个大问题:摄氏温标都用了那么久了,难道不考虑向下兼容一下?省得还要取修改那么多的东西。
的确是这样,懒人想法往往能避免很多麻烦。
哦,不对,得首先检查一下,有兼容的可能性吗?前面提到过,摄氏温标假设水银的体积随温度线性变化。上述温度函数是否也是如此呢?
我们来看,根据上述状态方程,当固定时,是的一次函数;当固定时,是的一次函数。好家伙,完美的符合摄氏温标的假设!其实,这两种情况分别是理想气体的另外两条实验规律:查理定律和盖·吕萨克定律。
08
理想气体温标
下面来看,如果要与摄氏温标兼容,上述理想气体状态方程中的常数和应该怎么取最好呢?
很简单,按照摄氏温度计找出两个不同温度的状态,测量出体积和压强,代入上式中求出和不就完事了吗?
不对!
如果真这样做,那不过是又得到了一种经验温标罢了!由于该温标与所用气体有关,故也需要对照摄氏温标进行校正。否则,据此制作的温度计,除了上述两个用来确定常数的温度值是准确的,其他的温度都是不准确的。
看起来这问题好像无解,因为现在只有两个待定常数,所以只需要两个温度值即可,但这样却又落入了经验温标的陷阱!
该如何是好?
想想,什么情况下可消除与气体的关联?
有了!上面提到的三个实验定律,在气体极稀薄时严格成立的,无论是什么气体。这告诉我们:只要气体的压强趋近于零,所得到的温标应该与具体的气体种类无关。
这意味着,若采用极稀薄的低压气体,通过测定两个温度下的体积(压强),应该能找到一个常规气压下无法获得的体积(压强)与温度的线性关系。
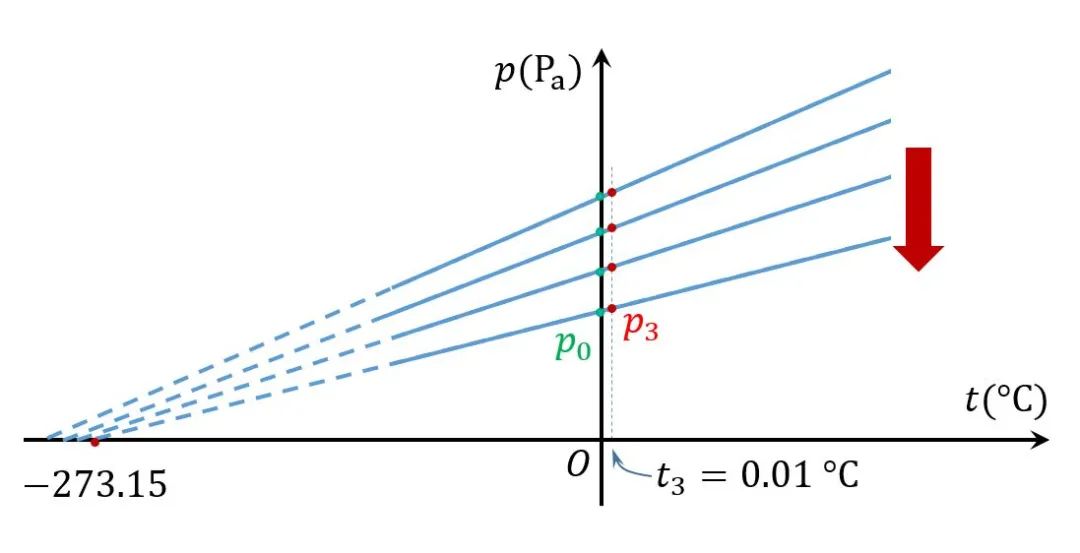
的确如此,通过不断测量更加稀薄气体的压强随摄氏温度的变化,人们发现,这些直线的延长线与温度坐标轴的交点无限趋近于一个固定点。经反复试验确定,这个点的对应的温度是-273.15 。若用表示气体在0的压强,则对应的直线的斜率是。即
同样,如果测量体积与温度的关系,也会得到类似的关系其中表示气体在0下的体积。
定义新的温标,即理想气体温标,用表示,单位为开尔文(K),令得理想气体温度为和现在一般采用气体在水的三相点处的体积和压强作为基准。由于水的三相点温度为0.01 ,在横轴上这个温度到极限温度之间的距离是273.16。故上面两式可分别写成
注意,这并不改变与的关系,二者还是相差273.15。
你可能觉得奇怪,为什么不选择273.15℃为基准温度?毕竟摄氏度和开之间的换算用的就是273.15这个数字,采用冰点温度作为基准不挺好嘛!
原因是,冰点、沸点这些点的温度没有三相点稳定。
需要说明的是,这里的所有的式子,都只在气体密度趋于零时才严格成立,也即是满足理想气体的条件才成立。
根据上述关系可知,任何气体在温度等于-273.15时,压强和体积都为零,显然这是不可能的。因此-273.15 实际上是无法达到的,这就是热力学第三定律。
至此,基于理想气体模型的温度标度——理想气体温标,确立了!
但是,真正的普适的温标——热力学温标(也称开氏温标),还未现身!
热力学温标需根据卡诺定理引入(后面再讲),但在理想气体温标范围(即气体温度计工作范围)内,热力学温标与理想气体温标完全一致。故现在可以提前使用诸如开尔文(温度的单位)、绝对温度(物理量T)、绝对零度(-273.15)这些名词了。
09
温标的矫正
由上可知,气体的压强(体积)与温度的关系并不是一条固定斜率直线关系,而是随着气体密度变化,斜率发生变化。
当气体的密度趋近于零时,得到一条反映理想气体温标的直线,其截距为273.15,斜率为气体在水的三相点处的压强(体积)除以273.16。
而摄氏温标,是在理想气体温标建立之前,人们依据一个假设存在的测温物质的属性与温度的线性关系建立的,但实际上这种线性关系并不严格成立,因此与理想气体温标之间是有差别的。必须予以矫正。
那应该迁就谁呢?
理想气体温标虽然受限于理想气体,但与气体种类无关,在普适性上前进了一大步。因此,它比摄氏温标更接近科学温标,故摄氏温标需根据理想气体温标进行校正。
那么问题就来了,既然摄氏温标所基于的线性假设实际上并不严格存在,也就是说,摄氏温标上有无数个点都与理想气体温标对不上,那该怎么矫正呢?
矫正方法是:先规定一些温度固定点,连同复现这些固定点的方法,组成所谓国际温标(ITS),然后按此温标进行矫正。基于任何温标的正常的温度计应能准确测出处于它的量程内的温度固定点。
最新的国际温标版本是ITS90,共含17个标准温度值。水的三相点温度273.16K就是其中一个标准值,因为它稳定且方便测量。而水的冰点温度就不是一个标准值,也就是说,水的冰点温度可以允许有一定偏差。
对其他的经验温标,也需要一样矫正。
10
理想气体状态方程
现在再看怎么得到温度关于和的函数,也就是将前面提到的状态方程完全确定。
将前面的温度函数按改写为设有摩尔气体,压强、体积和温度分别为,分别考虑等温、等容和等压过程,有
此3式相乘后开平方得
现考虑1摩尔相同温度和压强的气体,其体积为,据阿伏伽德罗定律,,则有由于是常数,计算得其值为。故得此即为著名的克拉珀龙方程,也称理想气体状态方程。引入玻尔兹曼常数和分子数密度,得此方程的变形形式为根据克拉珀龙方程得
此即理想气体的温度函数的最终形式。
到此,对温度的探讨暂时告一段落,但不要以为这就完了。以上只是基于宏观的层面,从热平衡概念引入温度的定义——热平衡的标志,并通过热力学第零定律引出了温度函数,在此基础上,借助理想气体这种特殊的物质,为温度建立了一种标度策略——温标。
但是,温度到底是什么?单个或几个微观粒子有温度吗?温度是否是大量分子集体所体现的一种效应?
另一方面,直觉告诉我们,温度应该是一种独立的物理量,因此它的定义和标度应该与物质种类和性质无关!否则的,温度凭什么适用于其他液体和固体?
所以接下来,一方面,我们应深入探讨温度的微观本质,这涉及统计力学。另一方面,我们应进一步探求一种普适的温标,它就是绝对温标。
11
热的本质
温差导致彼此间传热,那么到底什么是热?
第一种关于热的本质论的观点叫热动说。它认为,热是组成物质的微观粒子的运动的表现,可以通过机械运动转化而来。
这种观点在17世纪初被提出,例如英国的培根认为:
热本身,其本质和实质是运动,而不是其他什么。
眼光咋能这么毒!要知道,培根1626年就去世了,那时牛顿还活在他的上辈子中。
再例如,牛顿的宿敌胡克说:
热除了平动或转动,没有什么,热不是别的什么,而是物体各部分非常强烈的运动......
认识可谓相当深刻到位。
想象一下,你在墙上钉钉子,因为不停的敲打,钉子各个部分跟着振动起来,所以它变热了,玻意耳就是这样理解热的。
该学说的支持者有牛顿、莱布尼兹、笛卡尔、卡文迪许和托马斯·杨等人,阵容相当豪华。但奇怪的是,该学说竟然被另一个后来居上的学说给按在地上摩擦了两百多年,几代宗师们完全丧失了话语权!这究竟是怎么回事?
我们知道,温度不同的物体接触,原来低温和高温的物体分别升温和降温,达到热平衡,两物体具有统一的温度。那么,这过程中发生了什么呢?
一个容器隔成两半,左右分别装有压强不同的气体。当隔板上的阀门打开后,阀门处的气体受到的压力差指向压强小的一侧,于是压强大的一侧的气体流向压强小的一侧,直到两边的压强一致。
据此人们认为,温度不同的物体接触时,也发生了类似的物质流动——从温度高的一侧流向温度低的一侧。英国的布莱克认为,这种流质就是所谓“热质”,类似于当时被认为存在的电磁波的媒质——“以太”一样,它也是看不见的,没有重量的。
这就是历史上人们曾经对热的本质的主流观点——热质说。按此观点,温差驱动热质流动,热质到哪里,哪里就升温。热质本身不会创造,也不会消亡。
单位质量的物体含有多少热质,就会具有多高的温度,具体由物质的比热决定:若单位质量含有相同热质,比热大的温度低,比热小的温度高。
然而,摩擦生热给此观点当头一棒!来自美国的拉姆福德做了一个令人震撼的实验。他用一个钝钻头不停的切削一个大炮筒,2.5小时后,装在炮筒里的水竟然真的沸腾了。那问题就是,既然热质无法被创造,那温度怎么会升高呢?
为了解释这个问题,人们提出是因为摩擦使物体的热容量降低,因此温度就升高了。但1799年,戴维的冰块摩擦实验使热质说陷入真正的危机,因为摩擦得到的水的比热比冰还大,所以热质学说的基础——热质守恒是不可能的。
但即使如此,由于热质学说的影响深远,在这之后,傅里叶和卡诺以热质论为基础,分别建立了传热理论和卡诺定理。
直到四十多年后,一位毅力非凡物理学家投入了这场实验的长久战,他就是英国的焦耳。凭借他那异常精密的温度测量威廉希尔官方网站 ,他不断升级他的叶轮实验。直到1878年,他最终确认:做功与传热一样能导致物体升温。换句话说,热并不是什么流质,它与机械功一样,都是能量传输的途径。
12
热力学第一定律
根据热动说,热的本质是一种能量传递的方式,做功也一样。既然做功和传热都能等效的改变体系的能量,那很自然就会想到,体系的能量前后之间的差额不就是做功和传热之和吗?
这个问题在现在看来非常自然,这不就是能量守恒的思想吗?是的。但是,在历史上,这来得非常不容易。
很多人学完力学中的机械能守恒定律后就产生了一种想当然的错觉,以为在牛顿的时代,人们就认识到能量守恒了。实际上并非如此,直到18世纪,机械能守恒定律才被认可,而能量一词甚至到19世纪才由英国天才托马斯·杨提出。
19世纪,在焦耳正在做叶轮实验的那30年间,还有另外两位来自德国物理学家也在关注与热相关的能量问题,他们是迈耶和亥姆霍兹。最终,能量守恒定律被提出:自然界的一切物体都具有能量,能量有多种形式,可以从一种形式变成另一种形式,可从一个物体转移到另一个物体,但总量保持不变。
对于涉及传热和做功的系统,能量守恒定律可以表示为这里的本来要包含物体的动能,势能和与热有关的能量三部分,相应的也应该包含所有的外力做的功。但在热学范围,我们忽略物体整体运动,只考虑热运动的能量,因此只局限于热相关的能量,我们称之为内能,用表示,即其中是传热的量,正值表示吸热,负值表示放热。表示系统受外力做功,正值表示外力做正功,负值表示外力做负功。
顺便说一句,可能有人忘了,正功表示力在位移方向的投影的积累为正,负功则相反。如果外力是压力(例如大气压),当系统的体积增大时,是负的,而当系统的体积减小时,是正的。
这里面的和与过程有关,应该只取决于体系当前的状态。对微小的过程来说,这种关系依旧成立,此时三个量都变成无穷小量,表示如下其中功和热的微小量之所以用đ表示,因为这些量与内能不同,它们不是态函数的微分,只是微小量而已。
讲到这里,稍微再啰嗦几句。 我们知道,传热和做功与具体过程进行的每一步都有关,它们不是体系的状态决定的,而是由过程的每一步所决定的,因此决定这些量的因素有无穷多个。就像你从广场的东南角走到西北角,你所走的路径总长取决于你迈出的每一步。这类量就像含有无穷多个自变量的函数,我们称之为泛函,它的微小量叫做变分,数学上一般用表示,热学中也用表示。 因此,当你泛泛的说某个任意的热力学过程时,你必须清楚,做功和传热是一个泛函,而非函数,所以它们的微小量也不是微分。但当你特指某个具体的热力学过程时,由于你的过程的每一步是确定的,这些过程量就从泛函退化成函数,因此可以用微分来表示它们的微小量。
当过程进行得无限缓慢时,系统所经历的每一步都是平衡态,这称之为准静态过程。对这样的过程,系统的状态参量每时刻都有确定的值。
下面,我们以一个气缸为例来分析一下做功。
假设忽略摩擦力,它的活塞非常缓慢的移动,那么显然,来自外界的力时刻与气缸内的压力平衡,即
设面积为的气缸活塞向外发生位移,外力做功为
设气缸内的压强为 ,则注意:这里功的微小量之所以写成微分,因为这个过程是确定的,功虽然不是态函数,但却是一个普通的可微函数。
因此,对无摩擦的准静态过程,在过程完全确定时,每一步做功的大小是压强乘以体积的增量。若考虑到负号,即每一步做功是压强乘以体积的减小量。
既然这个确定的过程是准静态的,它的每一步都是一个平衡态,所以画在图上就是无数个点连成的一条线,沿着这条线积分,就得到过程的总功
然而,对于热来说,除了凭借经验测量,我们对它知之甚少。只有摸清了内能的由来,并建立热容量的概念,我们才能有办法从理论上对付它。
就热力学第一定律来说,它主要是表达一种能量收支平衡的关系,我们确信这一点。然而,这里面的究竟如何得到?也就是说,它如何被物体内的分子所持有呢?
是的,按照胡克的说法,它表现为微观粒子的运动,这正是热动说的落脚点。但问题是,只有动能吗?如果只考虑动能,又该如何分配?
要回答上述问题,必须先回答第一个问题是:物体内部的微观粒子真的在运动吗?有什么证据呢?
13
理想气体的微观模型
1827年,英国的植物学家布朗用显微镜观察到水中的花粉颗粒不停的游动。这种被称为“布朗运动”的现象起初被认为是生命力的体现,但随后人们观察到金属粉末也是如此。
随着研究的深入,人们推测:构成物质的微观粒子总在无时不刻的做无规则运动,这就是分子运动论。布朗运动正是因为这种微观粒子的碰撞在不均匀时所导致的,如下图所示,黄色小球就是一个正受到微观粒子碰撞的布朗粒子。

如果说这算是分子做永不停歇的无规则运动的证据的话,那么对这样的系统我们该如何研究呢?
我们不可能对微观粒子的个体进行追踪研究,而只能建立一种统计方法,对微观粒子的整体进行统计分析,这就是所谓统计力学。而布朗运动乃统计涨落的必然结果。
前面讲过,在利用宏观参量描述的热力学中,最简单的热力学体系是理想气体,即密度无限小的气体。现在用微观的统计方法,理想气体的微观模型自然也是最简单的系统。
理想气体微观模型是指:一、分子无限小;二、除碰撞的瞬间,分子之间无作用;三、所有的碰撞都是完全弹性的。
对解释热运动的统计理论来说,它最简单的版本就是以理想气体模型为基础建立的气体动理论。
14
随机事件与概率
为了建立气体动理论,必须先对随机事件、随机变量和概率及分布函数有所了解,所以这一节就专门列一下这方面的预备知识。
经典物理学有一条基本假设:粒子的未来的运动是可预知的。也就是说,只要知道受力情况,由当前的位置和速度能确定粒子以后的运动状态。这就是经典的决定论。
但在面对多个粒子组成的系统时,会出现三种非常规的情况。
一是,粒子之间的作用过于复杂,即使粒子为数不多,但作用导致粒子的运动对初始条件高度敏感,导致混沌现象。虽然此时决定论并未失效,但是已经没有实用性。
二是,当系统的粒子是彼此独立的,但粒子数达到天文数字级别,比如,虽然严格的讲,只要粒子不是微观粒子,决定论并未失效,但是由于粒子数太多,跟踪每个粒子已没有意义,粒子的运动可看作是随机的。
三是,当粒子是微观粒子时,即使是单个粒子,这种决定论也失效了,因为粒子是用量子力学的波函数描述的,根本不再遵循决定论。
经典的统计力学研究的就是第二种情况,基本数学工具就是概率论,利用随机变量的分布函数可以得到各种统计量。这里就简单的总结一下相关知识,具体自行查看相关资料。
a.做一件事,做了次,其中次发生了,当时,事件发生的概率为b.随机变量的取值在内的概率为,则定义附近单位间隔内的概率定义为的概率分布密度函数
c.若随机变量和是独立的,分布分别为和,则和的联合概率分布函数为
d.概率分布密度函数对随机变量的全空间上的积分为1,即归一化条件e.随机变量的函数的平均值为
15
温度的统计解释
现在先推导气体的压强公式,并据此推导出温度的公式。
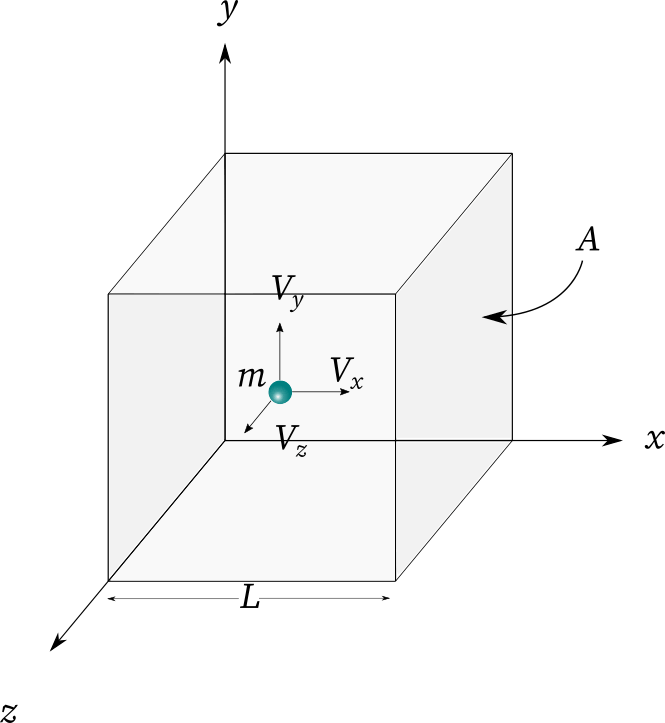
一个装有理想气体的容器,其垂直于轴的壁受到一个分子的撞击,分子反弹,其沿方向的分速度反向,其他的分速度不变,该分子给容器壁的冲量为。
设分子沿轴的速度分布函数为设单位体积内的气体分子数为,则那么,沿轴的分速度在内的分子数量为这些分子沿轴分速度可看作。
因此,单位体积内,沿轴分速度可看作的分子数为。则长为,底面积为的体积内,沿轴分速度取值为的分子数为这些分子将在的时间内都给容器壁施加冲量,则总的冲量为考虑不同的速度的粒子,将上式积分得总冲量,注意到只有的粒子才有机会与壁碰,故积分区间为,积分得在此冲量作用下,容器壁面元上受到的力为故上受到的压强为由于气体分子朝轴正反方向运动的概率相同,故
故得
理想气体分子处于各向同性的空间中,因此其各分速速的平方均值满足
故得其中是气体分子的平均动能(实际上,这只是分子动能的一部分——平动动能的平均值,此乃后话,暂且不提),至此,得到了理想气体压强公式。
联合理想气体的状态方程,得从此式,我们看到了温度的另一面,它的微观意义体现为大量微观粒子平动动能的平均值。粒子的热运动越剧烈,平均平动动能越大,温度越高!
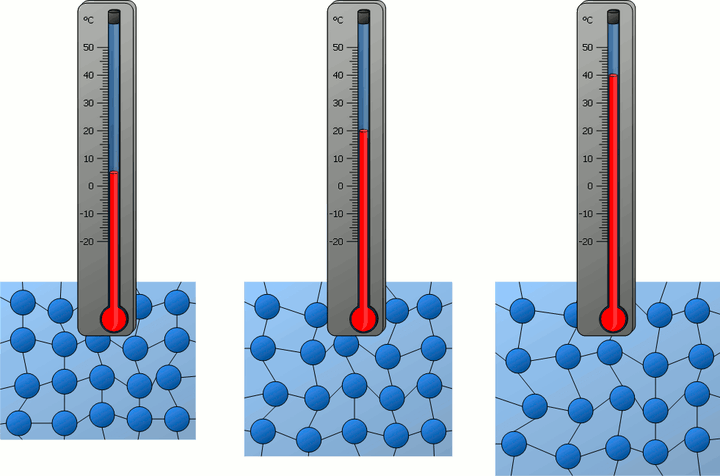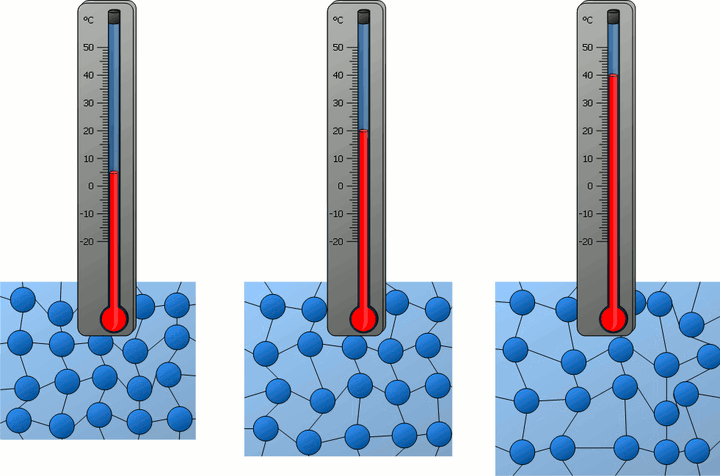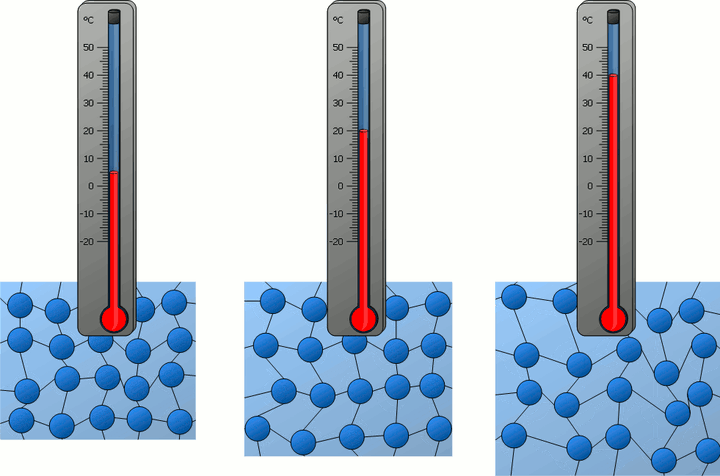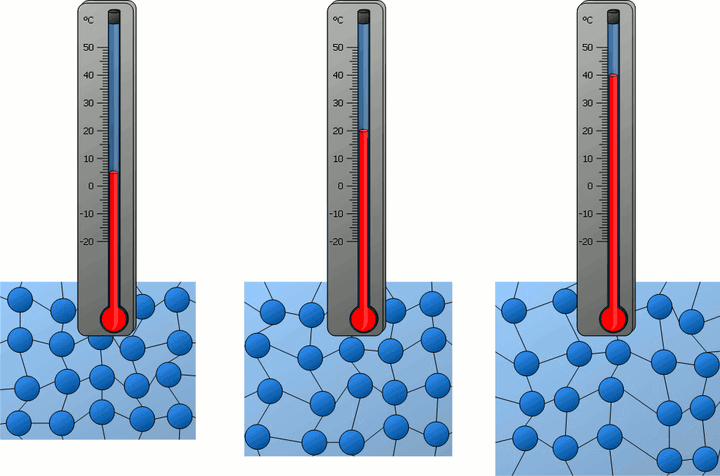
同时我们也看到,温度是一个统计量,它必须满足大数定律的要求,也就是说,要有大量的微观粒子参与,若只是几个粒子、几百个粒子的系统,温度是没有意义的。
我们还可以借此理解前面提到的热力学第三定律:绝对零度无法达到。因为用于求平均值的对象是动能,动能总是大于或等于零的,若要求平均值为零,则所有的微观粒子都必须静止,这是不可能的,因为统计力学假设粒子在永不停歇的做无规则运动。
行文至此,我们从热力学角度,阐述了温度的概念,并且从微观上解释了温度。但这种解释只是基于理想气体模型。然而,正如前面所说,我们应相信,温度既然是一种独立于物质种类的物理量,它应该具有更一般的物理意义,它的标度也应该独立于物质的种类。
所以接下来的目标是,如何确立一种普适的温标——绝对温标,并获得对温度的更一般的解释,从而得到温度的统计力学定义。达成这些目标,离不开热力学第二定律和熵的概念,而这又需要先了解循环过程及可逆过程的问题,下面一步步来讨论。
16
理想气体的内能
现在终于可以回答本文“热力学第一定律”部分所问的问题了,内能应该怎样被体系所含的分子们所持有呢?
对于理想气体来说,它的分子除了碰撞的瞬间,彼此之间是没有相互作用的,因此不需要考虑像各种吸引和排斥力造成的势能,每个分子只有动能。我们设想,内能就体现为全体分子的动能之和。
那么,分子可以怎么运动呢?
按照理想气体模型,分子是质点,质点是转不起来的——即使转了你也看不到。就像下面这个纯红色的球,若我说它正在转动,你看得出吗?转不转都不会有任何不同嘛,所以不存在转动。
因此,分子的动能就是质心运动的动能,即那么全体分子的动能之和就是内能了。根据速率分布函数,速率处于内的分子个数为故全体分子的动能之和,即内能为根据速率分布函数的意义,上式即为这时,想起之前关于温度的统计公式联立得若有摩尔气体,则分子个数为,则内能为此即理想气体的内能,可见它是温度的函数,当然也是一个统计量。
好了,现在热力学第一定律中的知道怎么对付了!它就是若此时回到热力学第一定律,我们有办法计算各种过程的传热了!于是我们可以从理论上得到摩尔的气体在任一个过程的传热,若体系温度变化为,可以定义此过程的摩尔热容量为例如,等温过程,由于 ,故
等容过程,,故
等压过程,,故然而,当人们将同一个放热过程得到的热供给不同的气体时,他们发现,对于像惰性气体,符合的较好,对多原子分子气体则相差较大!
数据偏差的规律一经研究,症结马上查明:相同温度下,多原子分子比单原子分子的平均动能更大!
很显然,多原子分子有形状,所以不能当作质点,因此,除了质心运动之外,它必然还有其他的运动!
首先是转动。学过刚体力学的人知道,与质点不同,刚体还有转动的动能。前面讨论分子的运动时,我们完全忽略了这一点。其实这也难怪,因为我们是在理想气体模型的框架下讨论问题的,气体分子被当作弹性小球,也就是质点了!
其次是振动,它是指分子内的原子相对分子的质心的运动。不过,一般来情况下,分子的振动很弱,可忽略,我们称之为刚性分子。理想气体分子就是刚性分子。
一般情况下,我们只考虑刚性分子,所以只需要考虑分子的平动和转动即可。
三维空间中,质点只能平动,确定它的位置需要三个坐标,因此单原子分子的运动需要3个参数来描述。而对多原子分子来说,即使你固定它的质心位置,它还可以转动。如果你想将其完全固定下来,还需要多的参数。
对双原子分子来说,描述转动还需2个参数。而对多于2个原子的分子,一般还需3个参数——除非是直线形分子,例如二氧化碳分子,如下图所示,它的转动只需要2个参数描述。
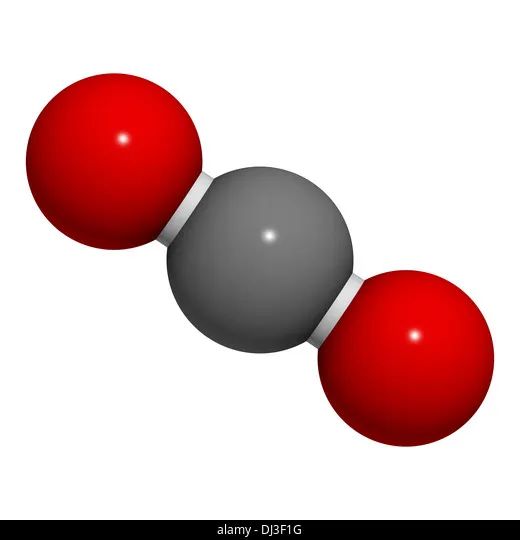
每个参数代表一个独立的运动,参数越多,表示分子受限越少,反之则表示分子受限越多。因此我们称这每个参数为一个自由度。
根据以上分析,对刚性分子来说,单原子分子、双原子分子和多原子分子的自由度个数分别为3、5和6(线形分子为5)。
对单原子分子气体来说,由于空间的各向同性,x,y和z三个方向上的方均速度相等,所以每个自由度占有一样的动能,因此其中是分子的平均动能。根据前面讲的温度的统计解释,所以单原子分子的每个自由度分摊的平均动能为。
但问题是,对于多原子分子气体,自由度不止3个,每个自由度平摊的能量是多少呢?
麦克斯韦和玻尔兹曼等人研究指出,能量被系统中各独立分量所等分。这就是所谓的能量均分定理。因此,气体分子的每个自由度都拥有一样多的平均能量,也就是。
据此,只要知道分子的自由度个数,则分子的平均动能为那么,摩尔的气体的总能量为根据前面所讲,等容过程的摩尔热容量为而等压过程的摩尔热容量为例如,对氧气,因为,故
17
理性气体的热力学过程
热力学第一定律源于能量守恒这一普遍的物理规律,因此它对任何物质所经历的任何过程都是成立的,例如炸弹爆炸这种非常剧烈的过程。
现在,我们再把对象范围缩小一点,让问题更加具体一些。
一方面,我们只考虑准静态过程,这样的话,过程中经历的每个时刻,体系都具有确定的状态,可对过程进行理论计算。例如外力做功总是可以写成(具体如何得到,见本文“热力学第一定律”部分)另一方面,我们只考虑理想气体,它的内能只是温度的函数,即所以,热力学第一定律(见本文“热力学第一定律”部分)现在可以写成大家看到,现在就剩下热量这个东西比较麻烦了。如果把它看做一个未知数的话,习惯上把它放在一边比较合适,所以把做功与内能放在同一边,得到注意,这里的做功的积分颠倒了,现在做功项表示气体克服外力所做功,它与外力所做功相差一个负号!上式现在可以理解为:理想气体从外界所吸收的热分成两部分,一部分用以增加气体内能,另一部分用以对外做功。
相比前面讲到的热力学第一定律,这个表示并没有实质变化,它依旧体现了能量的呃收支平衡。只不过,现在这里做功变成了气体克服外力做功,而前面做功是指外力克服气体压力做功。
在实际中(比如各种热机),我们要利用热力学过程做功,气体系统输出的功为我们所得,而气体系统获得的功为我们所付出,这样变一下,刚好将其分别表示为一正一负,看起来更直观合理。
因此,大多数热学教材上,热力学第一定律习惯被写成它给我们描绘了这样一幅图景:从燃烧的能源物质中获得热量,其中一部分拿来对外做功。
理想气体的典型的准静态过程主要有四个:等容、等压、等温和绝热。只要结合理想气体状态方程,我们能得到这些不同的过程中的传热、做功和内能的变化规律。
例如,等温过程的图如下。
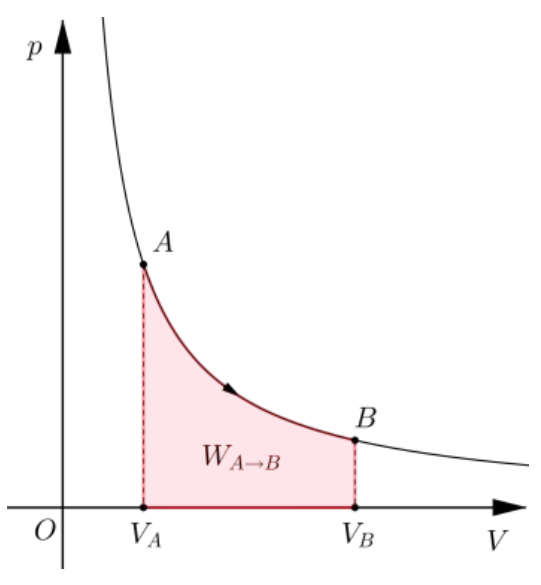
当理想气体从A沿着等温线走向B时,气体对外做功,但由于温度不变,所以气体内能不变因此,气体吸热时刻与对外做功的量保持一致这里的下标表示等温过程。顺便说一句,虽然一般的无限小做功和传热不是微分,但对于一个确定的准静态过程来说,无限小的做功和传热是微分。
根据理想气体状态方程可得计算得可见,在等温过程中,传热和做功一样,都是曲线下方的面积。
类似的,等容、等压和绝热过程的传热和做功也都可以得到,这里就不一一细说了。
18
理性气体的循环过程
如果基于热力学过程来提供机械功,单纯的某个热力学过程肯定不可持续。例如若仅靠等温过程做功,那么随着体积膨胀,气体的体积越来越大,你的热机将占据巨大的空间。
如果让气体经历循环过程,那么就可以避免这个问题。如下图,让气体从状态1出发,依次经历等温,等压和等容过程,回到初态。这个过程中,系统对外做功的值就是这个封闭路径围成的面积。
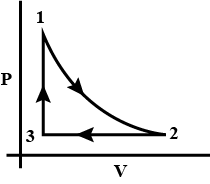
对一个完整的循环前后,系统状态相同,故内能不变,所以对外做功的值刚好等于从外界吸热的量。
值得注意的是,上述循环的三个过程有的吸热(例如1→2和3→1),有的放热(例如2→3);做功也是一样,例如1→2是对外做正功,但2→3是对外做负功。总体吸热多于放热,这才使系统能对外做功。
以上这种沿着顺时针方向行进的循环,叫正循环,它总的效果是吸热而对外做功。如果沿着反方向循环,那么总的效果就是接受外界做功并放热,称之为负循环。
对正循环来说,它对应热机,其吸热代表能量付出——例如燃油消耗量,做功代表获得的回报——例如所做的机械功。为了反映这种价值回报的比率,定义热机效率对负循环来说,它对应制冷机,其做功代表付出——例如用电,而吸热代表回报——例如冰箱中被吸走的热,定义制冷系数
一个小问题:为什么叫制冷系数而不叫制冷效率? 因为一般来讲,效率是指那种用百分数描述的东西,其最大也就100%,但制冷系数显然不受此约束,所以有还是换个名字比较合适。
你可能会问,有没有一种循环,它只有吸热过程,没有放热过程呢?如果真的有这种循环的话,那么上述热机的效率将是100%。
热力学理论和实践告诉我们,这是不可能的,因为这意味着,全部的热能都变成了功,这违反了热力学第二定律(即将讲到)。
卡诺提出一种最简单的循环,它只与两个不同温度的热源发生热交换,因此,除了两个等温过程之外,它只包含绝热过程。这种循环叫卡诺循环。
对理想气体来说,如果考虑准静态循环,那么卡诺循环就由两条等温线和两条绝热线构成。其中,正的卡诺循环如下所示
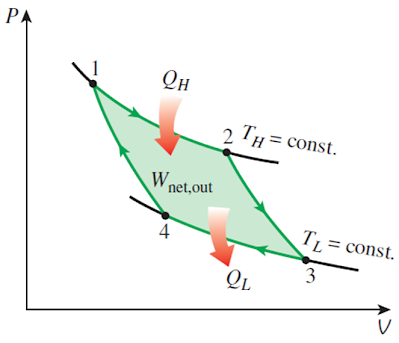
它的效率为而负的卡诺循环(依旧考虑理性气体的准静态过程)则表示为
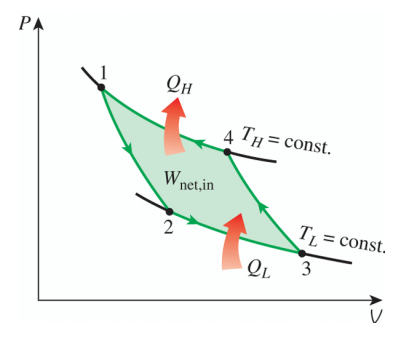
基于它工作的制冷机的制冷系数为除卡诺循环之外,还有很多其他的循环,例如奥拓循环,斯特林循环等等,它们的热源个数都不止两个,具体细节在此不再赘述。
19
热力学第二定律
大家都知道,破镜不能重圆,覆水难收。李白曾写道:“长江之水天上来奔流到海不复回”。生活经验告诉我们,自然的过程一旦发生,无法恢复。换句话说,自然界的宏观过程都是不可逆的。
例如,铁球从高处落下最后停在地面,它的机械能通过碰撞变成热,即使你保留这些热,你也无法重新让球获得它原有的机械能而飞起。
杯中的热水将热传给它周围的空气而冷却,但你永远都不会看到空气中的热又重新聚集到杯中,水自动又热起来。
是的,自然界的宏观过程的不可逆性是显而易见的!但一开始并没有一个物理规律能解释这种不可逆性,因此人们需要一条新的物理定律对此予以确认。这个规律就是著名的热力学第二定律。
基于热传导的不可逆性,德国的物理学家克劳修斯在1850年给出的热力学第二定律的表述为:
热不可能自动从低温物体传到高温物体。
英国物理学家开尔文于1851年提出的另一种版本的表述为:
不可能从单一热源吸热并100%变成有用功而不产生其他影响。
可用反证法证明,这两种表述本质上是等价的。具体方法是,证明命题的逆否命题相互等价,那么原命题就等价。此处不表,可参看相关资料。
其实,任何两种热力学过程的不可逆性之间都是等价的,因此,热力学第二定律可以基于任何一种宏观过程来表述。
关于宏观过程的不可逆性以及热力学第二定律,另一篇文章“可逆与不可逆:我们为什么回不到从前?”有较详细的解读,可参考。
20
卡诺定理
1824年法国青年科学家卡诺提出,工作在两个温度和之间的一切卡诺热机中,可逆热机具有最高的效率,此即卡诺定理。
由卡诺定理可知,任何可逆的卡诺热机的效率都相等,而以理想气体为工作物质的可逆卡诺热机的效率为因此卡诺定理的数学表示为
左边代表一般卡诺热机的效率,右边代表可逆的卡诺热机的效率。
你可能会问,如何证明卡诺定理呢?
其实,有了热力学第二定律,我们就可以推出卡诺定理——虽然历史上,它并不是这样得到的,因为那时还没有热力学第二定律。
基于热力学第二定律,借助反证法,可以很容易证明卡诺定理,具体过程此处从略,有兴趣可参看文章“从卡诺定理到熵增加原理”的第1~3节。
21
热力学温标
以上从讲完“温度的统计解释”之后,就几乎与温度关系不大了。但现在,我们又要回到温度这条主线了!是的,前面这好几节的内容都是为了引出本节这个至关重要的内容。
前面讲到了两种温标,第一个是经验温标(摄氏温标),以某种物质的特定属性为基础建立起来的温标体系;第二个是理想气体温标,它是基于理想气体建立的。理想气体并不是一种具体的物质,但终归是气体嘛,所以这两种温标都与物质的种类有关系。
但我们始终相信,温度度作为热平衡的标志,应该是一种普遍的属性,因此应该建立一种与物质本身无关的温标体系。
现在机会来了,它就是卡诺定理。
根据卡诺定理,任何工作在具有确定温度的两个热源之间的可逆卡诺热机的效率都相等。如果卡诺热机的效率是一个函数的话,那么这个函数只可能是两个热源的温度的函数,与热源的物质类型无关。
英国物理学家威廉·汤姆森(后称开尔文勋爵)意识到,根据可逆卡诺热机的效率,可以建立一种独立于物质性质的温标。
假设在某个任意的温标下,两个热源的温度值分别为和,既然可逆卡诺热机的效率
是和的函数,那么放热与吸热的比应该也是和的函数,即如果再引入一个新的热源,假设它的温度为,现在有两台热机串联,第一台热机放热作为第二台热机的吸热,第二台热机放热,同时这两台热机合成一台总热机,它吸热,放热。
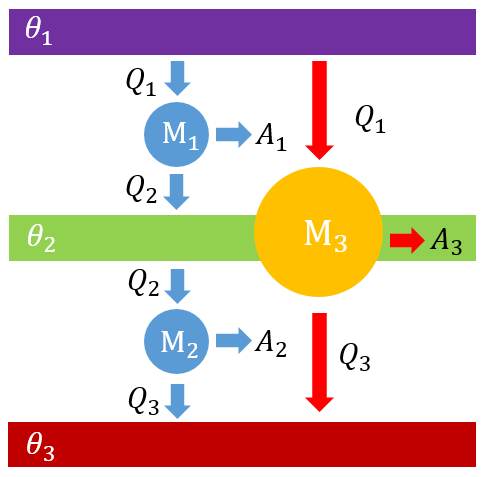
类似于热机,对热机和分别有联立以上三式可知上式右边的没有出现在左边,说明它应该是被消掉了,所以函数应该具有以下形式其中是一元函数,因此到此可知,这种建立在温度上的函数就能给出一种新的温标,即选取不同的函数作为温度值,就会得到不同的温标。只要它们给出的温度值的比等于相应的热源的热交换的比即可。由于热与物质性质无关,所以这种温标给出的温度值不依赖于物质的性质。
换句话说,我们终于第一次跳出了物质的圈套,找到了一种普适的东东,用以标度温度,它就是热量!
不过,正如在讲质量问题时提出的,标度并不一定具有实际可操作性,由于热量的测量离不开温度,所以这种标度本身只具有理论意义。
但到底如何选择?除了要满足之外,并无要求。换句话说,这种普适温标有无数种!
由于这种普适温标只给出温度值的比,没有给出温度的实际值,要给出温度的实际值,需要一个参考点。
那么,该如何选择这个参考点呢?
这时候应该尊重历史!就像理想气体温标兼容摄氏温标一样,现在这个好不容易发现的普适温标如果能兼容理想气体温标就好了!
这个能否做到呢?
能!
根据理想气体的可逆卡诺循环,有
注意,这里的温度和是理想气体温标下给出的温度值,之前讲理想气体温标没带撇,现在带撇是为了与新的温标下的温度值区分开来。 所以得到
太好了,普适温标下温度值的比竟然刚好与理想气体温标下的温度的比相同!
诸君再想想,二者比例一致,如何让二者的值也一致呢?
答曰:只要让它俩针对同一个特征状态点(温度非常稳定的状态)所给出的温度一致即可!
那么再回想一下,理想气体温标选择了哪个基准温度值?
没错,水的三相点温度——0.01摄氏度!也就是于是,1954年,国际计量大会决定,普适温标给出的温度用开(K)作单位,并规定水的三相点的温度值规定为273.16K,新的标度下的温度值确定了!
这就是开氏温标,也叫热力学温标。由于它采用的温度标度独立于物质性质,所以也称绝对温标。
由于热力学温标与理想气体温标选择的基准温度一致,并且比例又一样,那么自然就有这说明,在理想气体温标能用的范围内,热力学温标与之一致!正因为如此,在很多时候,我们不再区分理想气体温标和热力学温标,它们所表示的温度都统一用表示,单位都是开。
绝对温标不仅仅给出了一种独立性的温标体系,它还有助于加深对温度含义的理解,在这里也简单的说几句。
从绝对温标下温度值满足的关系可知,两个热源的温度比反映了卡诺热机与两个热源交换能量的比例。换句话说,热力学温度是决定可逆热机效率的唯一因素。
当时,,此时热机做功,热机效率为100%,这违反了热力学第二定律的开尔文表述,可见温度不可能达到绝对零度,只能无限接近,这说明热力学第二定律与热力学第三定律是一致的。
当时,,热机做功,热机效率为零;反过来,效率为零的可逆热机,其连接的两个热源的温度相等,这说明,温度相同不仅是热平衡的标志,还是可逆热机效率为零的标志。
至此,我们完成了本文的第二个重要任务——建立了普适的热力学温标。然而,温度从微观层面上到底如何理解?
别忘了,前面得到的“温度反映分子热运动的平均动能”这个结论是基于理想气体模型!现在既然建立了绝对温标,温度不再局限于理想气体了,那该如何更好的理解温度的本质呢?
为了回答这个问题,我们换一种角度来定义温度,而这个定义离不开另一个可能比温度更重要的物理量——熵!
22
克劳修斯熵
法国天才卡诺的发现不仅让开尔文猛然醒悟,更是令德国物理学家克劳修斯茅塞顿开。实际上,克劳修斯比开尔文更早意识到卡诺的发现的伟大价值。他发现,热力学第一定律作为热力学的基本定律是不够的,必须再来一条,它就是热力学第二定律,这样才能在抛弃“热质说”后仍保证卡诺定理成立。
基于卡诺定理,克劳修斯发现,任何一个循环,热温比的积分满足
这就是因他而得名的克劳修斯不等式。等号在循环是可逆的时候成立,而小于号对应于循环不可逆的情形。关于它的证明,在文章“从卡诺定理到熵增加原理”中给出了详细的过程。
根据克劳修斯不等式,对连接两个确定态的任意可逆过程,热温比的积分值是确定的,这说明必然存在一个只与状态有关的函数,它在两个态的取值之差等于热温比沿任意可逆过程的积分,即
可逆đ
这个状态函数就是熵(Entropy),也叫克劳修斯熵或热力学熵。上式即为热力学熵的定义式。对一个微小的可逆过程来说,熵的微分就是热温比,即
对经历的任意过程1→2来说,基于克劳修斯不等式可以发现,热温比的积分不会比熵的增量大,即关于该式的证明过程,读者可参看文章“从卡诺定理到熵增加原理”的第6节。据此式可知,当某一个过程绝热时,系统的熵增量不会为负。
由于孤立系统是绝热的,因此上式也就意味着,对实际的不可逆过程,熵一定会增加,即这就是熵增加原理。
虽然熵的值本来只与状态有关,但现在没法知道它到底如何由状态决定,所以只能通过计算热温比的积分来获得它在不同态之间的差值。
根据热力学第一定律,再结合熵的微分关系可知此式将热力学第一、第二定律结合起来了,只包含状态量,称之为热力学基本方程。根据此方程,可以通过构造合适的可逆过程来计算不同态之间的熵差。
举个例子说明一下。
一个用绝热材料制成的容器被隔板分成两半,当隔板去掉后,左半部的1mol的气体就会扩散到右半部,计算前后状态之间的熵变。
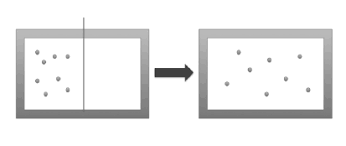
设这1mol气体的初态为,根据热力学第一定律可知,前后两个态内能相同,故温度相同,由玻马定律得末态为,可以构造一个等温过程来连接这两个态,故熵增为计算得,结果为正,熵增加了!
然而,计算归计算,大概也没什么好说的。但问题是,仅从上面的定义,似乎看不出熵代表什么意义!那么熵到底是什么呢?
23
玻尔兹曼熵
你可能意识到,熵增加原理意味着一种不可逆性,那么,它本质上是否就是热力学第二定律?
没错!自然界中的宏观过程都会朝着熵增加的方向进行的,正因为如此,所有宏观现象都是不可逆的,所以熵增加原理本身就是热力学第二定律换一种角度的说法罢了。
例如,上节的例子,气体从容器的一半扩散到全部空间中并趋于均匀,这个过程不可逆,熵增加了。再例如,密度不同的气体混合后,成为密度均匀的气体,这个过程也是不可逆的,熵必然增加。
想想,这些过程有什么共同特点?
没错!系统都是朝着气体分子更加趋向均匀的方向演化!
什么叫更加均匀?就是大量分子趋向于分布在更大的空间。如果统计任意时刻所有分子的坐标,你会发现,它们的分布趋向于均匀分布,换句话说,气体分子更加混沌,更无组织,更加无序。
这说明,熵增加与更高的无序度对应,也就是说,熵代表一种无序度。
那么,具体如何将这种无序度量化,并且与熵联系上呢?
我们先来看两个概念:宏观态和微观态。
将4个小球放在分为两半的容器中,每个小球有2种放法,所以共种放法,我们称每种放法为一个微观态,所以共有16种微观态。我们把左右球数记为有序数对,不同的数对代表不同的宏观态,因此共有5种宏观态,如下图所示。
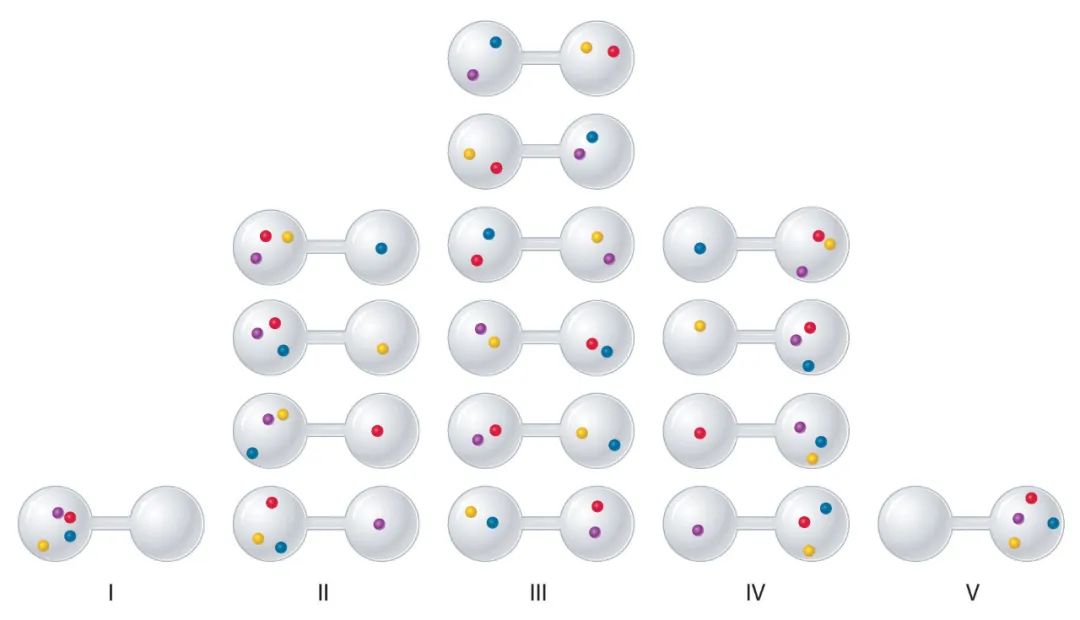
很显然,对于宏观态(4,0)和(0,4)来说,都各只包含一种微观态。但对(2,2)来说,它包含了6种微观态。
总地来说,微观态是指一种具体的安排,即让个体各就各位,在统计物理中这叫配容。而宏观态是指一种分类,它只管各类分别有多少,而不管到底谁属于哪个类,在统计物理中这叫分布。
假设每个小球完全随机的选择容器的左右半部,换句话说,这16种微观态以同样的概率出现——统计力学中的“等概率假设”,那么自然的,那些拥有较多微观态的宏观态出现的概率大一些,例如(2,2)的概率是6/16,而(4,0)或(0,4)的概率都只有1/16。
如果小球有10个,则微观态数有1024种,宏观态数有11种,其中(5,5)出现的概率为252/1024,(6,4)出现的概率是210/1024,但(10,0)或(0,10)的概率只有1/1024。
根据组合知识,从个小球选择个放入左侧的方法数是这就是左右边分别放和个小球的总方法数。很显然,当 等于(如果为奇数,二者相差1)时,上式分母取最小值。即分布均匀的宏观态,取最大值。
温馨提示:这里涉及高中数学两个知识,一个是计算组合,另一个是,考虑若干个和为常数的整数,当它们相等或最接近时,它们的乘积最大。
而既然总的微观态数是确定的(),每个微观态数的概率也都是确定的(),那么取值最大的那个宏观态的概率()当然是最大的。
如果容器被分成个间隔,设第个间隔里放入个球,则个球全部放入这些间隔的总的微观态数当然就是,而任一个宏观态的所i包含的微观态数就是同样,当所有的都相等或尽可能接近时,取最大值。
所以,分布越均匀的宏观态,出现的概率越大。对大量气体分子来说,它们之所以从容器一侧扩散到整个容器,也是因为越均匀的宏观态,包含的微观态数更大,所以出现的概率越大,因此,这种分布叫最概然分布。
为什么气体分子不会自动聚集?因为概率太小了!
可根据容器被分成两半的情形来验证一下。假设有1mol气体,它有阿伏伽德罗常数个分子,全部分子回到容器一半的概率为
这么小,完全可忽略!
你可能会认为,如果让左半部比右半部只多几个分子,这种宏观态出现的概率应该不会太小吧?例如前面的4个球的例子中,左边3个右边1个,概率也有高达1/4哦!
实际上,若计算就会知道,只要分子数目达到阿伏伽德罗常数的级别,那种情况的概率几乎为零。至于4个球的例子之所以会导致比较大的概率,是因为球的总数太少。
按照克劳修斯的熵增原理,气体扩散之所以不可逆,是因为熵增加;而现在又知道,这是因为系统的微观态数增加了,也就是变得更混乱了。任何孤立系统,只会变得更混乱,而不会变得更有序,这是符合我们的经验的。
如果这两种理解是一致的,那么意味着,熵与混乱度是正相关的。如果微观态数是混乱度的量化表示,那么熵必然与微观态数之间有一种对应关系。这就是奥地利物理学家玻尔兹曼所意识到的。
然而,熵与微观态数之间究竟有怎样的关系呢?
熵与内能一样,属于广延量。例如,当你把两个系统看成一个系统时,总系统的熵理应是两个系统的熵之和。即但这两个系统合并之后,微观态数是按照组合的乘法原理来计算的,即玻尔兹曼利用对数的性质提出一种熵,即这就是玻尔兹曼熵,它与微观态数的对数成正比。那么这个比例系数是什么呢?
这个问题不太难。再次回到上节所讲的那个气体扩散的例题,现在用玻尔兹曼熵来计算熵增,设比例系数为,则气体扩散前后的熵分别为根据斯特林近似得熵增为
既然玻尔兹曼熵与克劳修斯熵一致,则
得故得最终的玻尔兹曼熵的定义式为可以证明,它的确与克劳修斯熵是一致的,有兴趣可参看北大刘玉鑫教授的《热学》的第5章的5.5.2节,这里就不涉及了。
与克劳修斯熵不同的是 ,玻尔兹曼熵给出了熵的绝对值。并且,玻尔兹曼熵更能清晰的反映熵的本质。因为玻尔兹曼熵与体系的微观态数的对数成正比,所以体系包含的微观态种类越多,也就是越混乱,熵就越大。
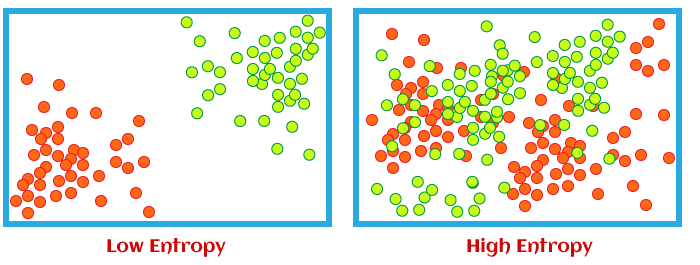
所以,玻尔兹曼熵更清晰地体现了系统地无序程度,或者说混乱度。
有了玻尔兹曼熵,对于熵增加原理的理解就更直观了,孤立系统总是朝着包含微观态数更多的宏观态演化,因为那些宏观态出现的概率大。
自然界的一切过程,都会导致熵增加。地球上的人和生物之所以能维持低熵,盖因不断向周围排熵所致也!总的来说,一个生物和它的周围环境的总熵一定是在增加的。
熵的意义太深奥了,为了避免延申过多造成不适,这里就先打住吧。
24
温度的统计定义
本文到目前为止,热学中最重要的三个物理量都已经讲的差不多了。它们分别分别是温度、内能和熵。
温度是热平衡的标志,所以一般说来,没有热平衡就不要谈温度了。温度的定义中“冷热程度”四个字不是嘴上说说而已,它必以热平衡为前提。否则,你肯定会问:难道一个没有达到热平衡的体系没有冷热程度?
不过说到内能,虽然对理想气体来说,内能与温度同进退,但根据普适的热力学第一定律,热能不应该取决于体系是否是热平衡,毕竟能量又不会消亡也不会被创造,它是那么实在!
再说,熵呢?熵既然源于体系的微观态数,没有达到热平衡也有微观态数,所以任意宏观态都有熵。实际上,普朗克当年给出的玻尔兹曼熵的表达式中的就适用于任何情形的。
讲到这里,似乎有一种感觉,那就是,温度这个物理量有点怪啊!它必须依赖于热平衡。只是在热平衡时,温度才存在,这让人感觉不那么实在。没有内能和熵那样实在。
那么,比起内能和熵,温度是不是没有那么基本呢?
这个当然是个容易引起争议的话题,这里就当抛砖引玉吧。不过,这的确让温度看起来越发神秘,是啊,温度到底是什么呢?
我们不妨换一个角度来重看温度,这就是本节的任务——温度的统计定义!
前面讲完克劳修斯熵之后,给出了一个可逆的微观过程所满足的公式稍作变形就是由于内能是态函数,如果取熵和体积作为它的自变量,则内能的全微分为将上两式对比可知这,就是温度的另一种定义:温度是内能随熵变化率!
它告诉我们,系统在等容变化——也就是只有热交换时,体系的内能之所以增加,是因为体系内部的混乱度提高。而温度就是表示这种混乱度对内能的贡献。
当内能随体系的混乱度变化越快时,温度就越高,反之温度就越低。另一方面,温度越高的体系,体系的混乱度稍微改变一点,可造成能量的大幅改变。
打个比方,故事已经达到最高潮了,这时候若某个步骤稍微被打乱,结局就完全不同了。另外,在最紧要关头,人越容易犯错,当然也容易突破。
遍布于体系中的熵,也就是混乱度,就好似是一种容纳能量的容器,它单位容量能容纳多少能量,取决于体系的温度,温度越高,这些容器中装的能量就越多。
换句话说,温度就是无序化的能量!
物体具有各种形式的能量,例如电磁能和机械能,动能和静能等,现在还可以根据无序化的程度来区分。
一个发热的红外理疗灯,它的无序化能量——热能占比太多,所以它的温度就高。我们需要冷光源来照明,以保证更多能量以更有序的光能的形式发出。
两个运动的小球,它们的无序化能量占比不高,所以温度不高,但它们碰撞之后,温度升高了,因为无序化的能量占比大幅升高!
呃,现在你对温度是不是有了不一样的认识?
不过,讲了这么多,温度似乎还是很局限,难道温度只能对普通的物质分子构成的宏观体系才可以定义?
不是的,任何系统都有温度,例如光子、电子、甚至夸克等构成的体系。因为温度是一种普适的物理量。
要认识到温度的普适性,需要介绍相应的统计理论,我们先来看看最简单的那个统计理论——麦克斯韦-玻尔兹曼统计吧。
下面先来讲一讲麦克斯韦速度分布率。
25
麦克斯韦速度分布律
在前面推导压强公式时,用到了沿的速度的分布函数的概念,但并未给出具体形式——当然那时并不需要。实际上,平衡态的理想气体的分子的速率应该服从某种特定的分布,否则无法满足压强和温度的公式。
那么,这个分布应该是什么样呢?
最容易想到的是均匀分布,也即是速度从零到某个极限值,都以一样的概率出现,其实,简单的想想我们自然界的一条普遍规律:能量越低越稳定,反之亦反。因此,气体分子的速度不可能是均匀分布的。
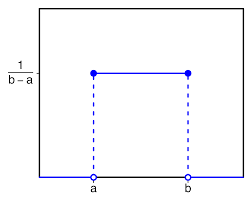
还有一种猜想是:所有分子的速率围绕某个值取值,也即是正态分布,因为生活中这种分布太常见了,例如某个国家成年人的身高就是如此。
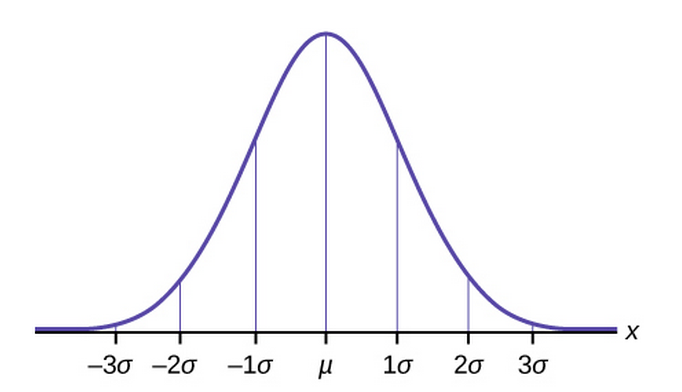
第二种猜想与结果相符,气体分子的速度分布——麦克斯韦速度分布的确就是一种三维正态分布。
麦克斯韦的直觉强大,据说他直接猜出气体分子的三个分速度的大小是高斯分布(正态分布),如果直接接受这一点,那当然可根据平均动能的结果得到最终的分布函数。
关于麦克斯韦分布的推导,很多书上给出的过程都过于跳跃。若这里讲推导过程,那本文的数学重口味指数瞬间飙升太高,还是忍了吧。如果你有兴趣可以参考B站北大欧阳颀院士的热学课,北大赵凯华教授的新概念物理学教程《热学》中也有详细推导。
从这些推导可以看出,只要承认速度分布满足各向同性,就必然得到速度分布函数具有如下形式而根据分布函数的归一化条件,以及前面推得的理想气体分子的平均平动动能为这一结果,可以推出上式中的待定常数和的值,从而得到分布函数的表达式。
这里直接给出该分布函数读者一眼看出,速度分布正好是三个独立的分速度的分布函数的乘积,即其中三个分速度的分布函数为这是独立的随机变量的联合分布所满足的乘法关系决定的。可以看出每个分速度的分布函数是一样的,都是正态分布——不要说你不知道什么是正态分布哦。
根据上述分布函数,处于速度空间的体积元内的分子的概率为
将此式换为球坐标系,得
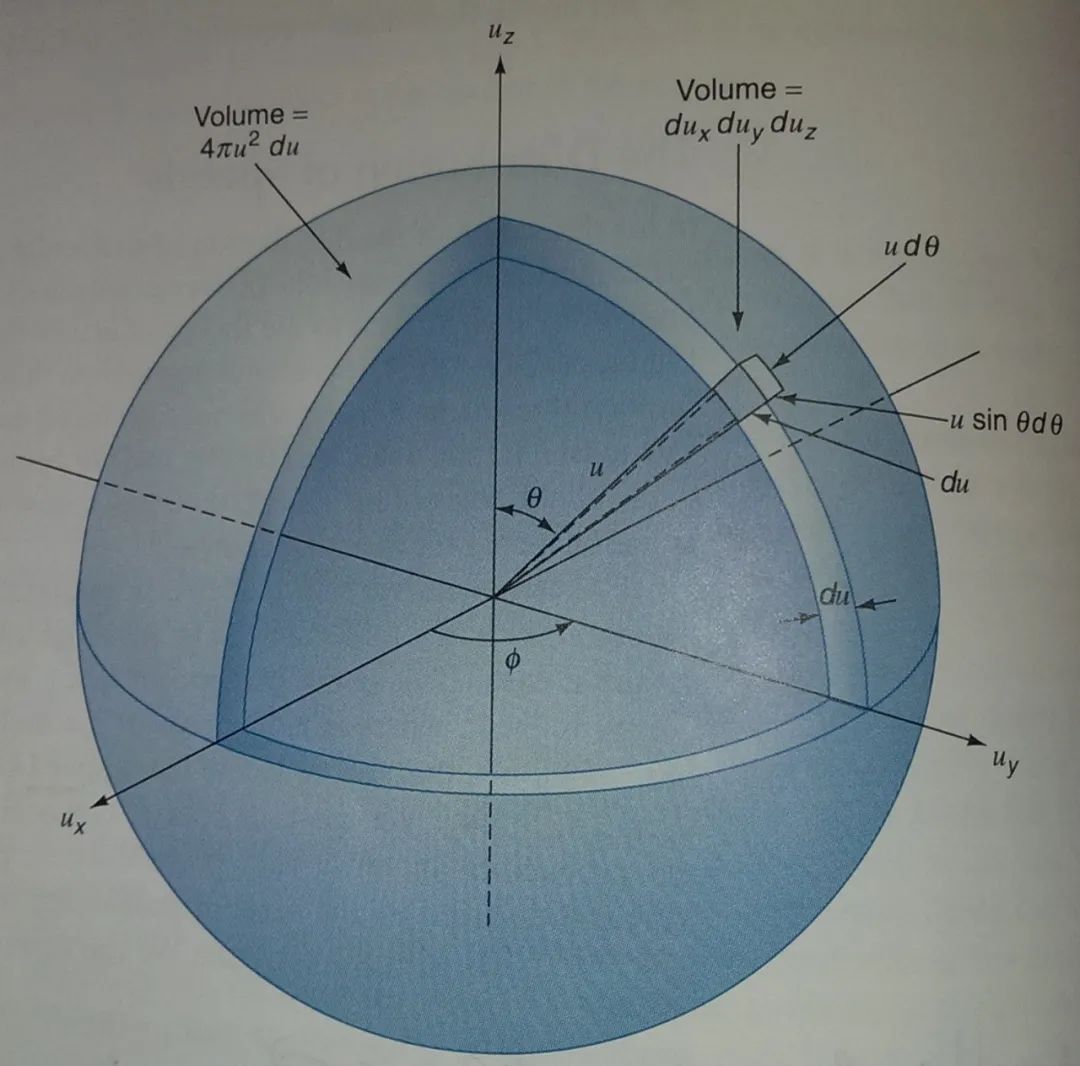
据此式,将和积分掉,则得到速度处于一个薄球壳内的概率,即故得气体分子速率分布函数为
注意:为了简便,本节中的符号依变量不同而表示不同的分布函数。
从麦克斯韦速率分布,可得到最概然速率,平均速率和方均根速率分别如下下图展示了它们的大小顺序。
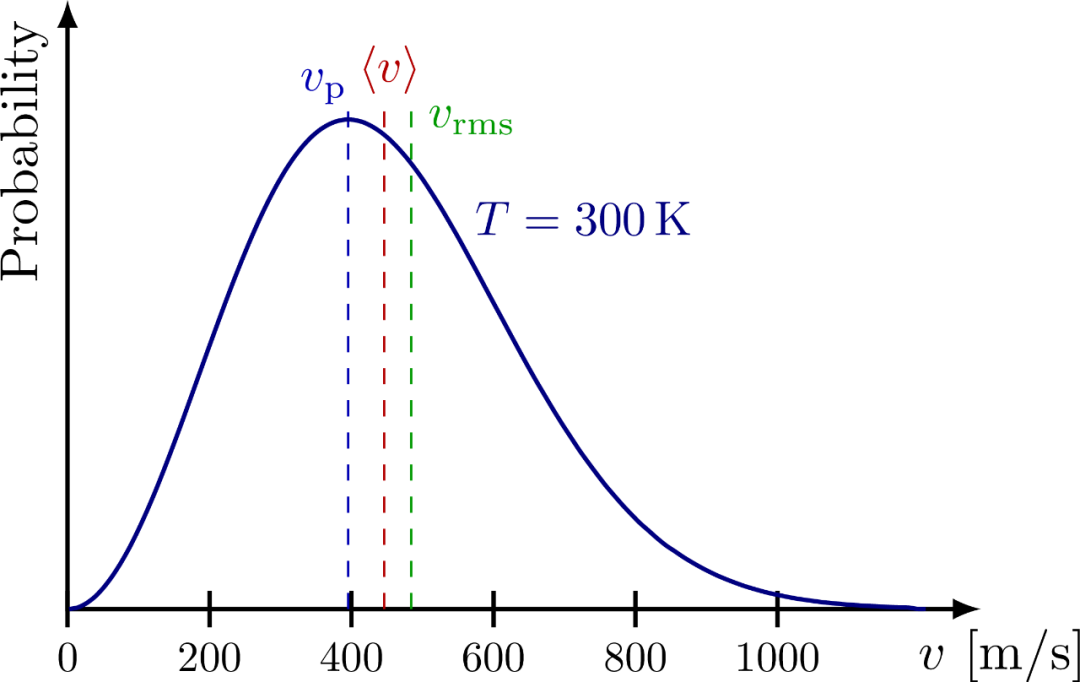
如下图是某种气体在三种不同温度下的分子速率分布曲线。
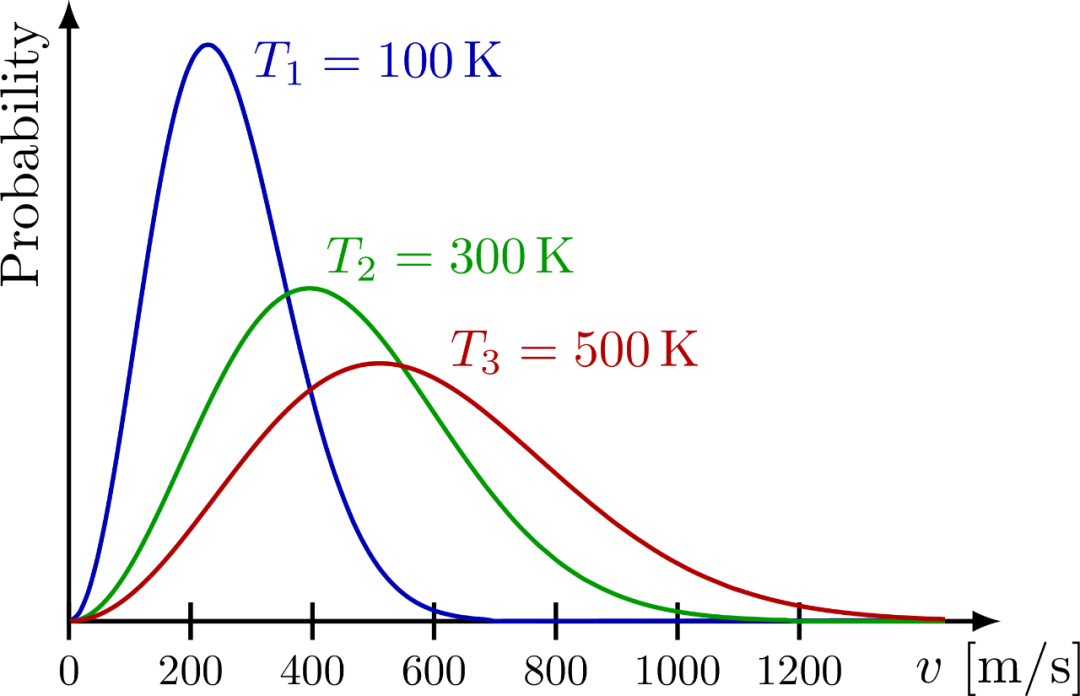
上节提到,温度是统计量,而麦克斯韦分布就是统计的结果,所以它必然体现温度的影响。正如上图所示,分布函数中的的指数中的越大,气体分子的最概然速率越大!
其实,这是一种普遍的规律。对不同的热平衡系统,例如光子气、电子气甚至夸克胶子等离子体(QGP),我们总可以根据某个量的分布来确定该系统的温度。
是的,温度不依赖于物质粒子,只要有光,真空也是有温度的!
为了让你对此有所了解,有必要说说统计力学的基本问题。
26
一般的分布和统计方法
麦克斯韦给出了理想气体分子的速度分布律,但它只是一种更一般的分布的特例,这个分布叫麦克斯韦-玻尔兹曼分布,简称M-B分布。
说到这里,有人可能会倒吸一口凉气,一篇文章而已,真的要讲这么多这么硬核吗?
真的要讲统计物理?那是不可能的!但完全不讲,那也是不可能的!!
考虑到很多人可能也没学过统计物理,本文就尽量用比较通俗易懂的语言说说统计物理的主要思想、目的和方法。理解不到位之处,请轻砸。
说明:在前面的一些节中,也涉及了一些统计相关的知识,例如在“随机事件与概率”部分介绍的数学知识,在“玻尔兹曼熵”部分介绍的有关“微观态”、“宏观态”以及“等概率假设”等知识,本节不再重复。
我们知道,热力学理论是基于实验事实归纳总结出来的,它的核心是热力学第零、第一和第二定律。三条定律分别给出了温度、内能和熵这三个态函数,并且得到了描述可逆过程的热力学基本方程。
然而,理论物理学家对此并不满足,他们希望这些规律能从某种基本假设经过推理和演绎得到。就像牛顿力学,人们通过最小作用量原理、对称性和相对性这些基本假设,建立了更加系统化的经典力学的理论体系。
你可能认为,既然热力学系统是由微观粒子组成的,那么从微观粒子所服从的力学规律出发,应该能得到宏观的热力学规律。
但实际情况并非如此,由大量粒子构成的热力学体系,除了受到单个粒子所服从的力学规律的影响,还具有许多新的性质,它们源于大量粒子构成的整体所具有的统计规律。
所以,微观粒子构成的体系有两方面的性质,个体的性质和整体的规律。
个体的规律,就是力学规律。至于什么类型的力学规律,准确来说当然是量子力学啦,因为它就是专门处理微观粒子的理论,但有时,牛顿力学也可以用。
整体的规律,就是统计规律。它是由个体多到一定程度时集体体现的,所谓量变引起的质变,而体系的宏观性质更多由它决定。
那么具体来讲,到底什么是统计规律呢?简单的说,就是采用统计平均的手段所得到的规律。
例如前面关于理想气体的压强、温度和内能的微观解释的数学表达式,还有气体分子的平均速率这些,都是统计规律。
不过,这些都不是最一般的统计规律。统计力学的最一般规律,就是指微观粒子的分布的规律。
什么是分布规律?前面讲玻尔兹曼熵时说过,这里再详细说说。
我们将粒子(比如个)的所有可能的状态看作某种空间中的点,如果该空间被分割称很多格子(比如个),那么这些格子分别落入了几个粒子?如果用表示第个格子里的粒子数,所谓分布就是如下的数组
一般这个数组可用一个函数表示。达到这一步,分布就算到位了。
当然,这个空间是什么空间(空间还是空间),格子又是什么格子(相空间体积元还是能级),就要看具体情况了。
这里的空间是一种状态空间。在经典力学中,粒子的每一个自由度对应一个坐标和动量,分别用和表示。以它们为轴张开一个空间,叫相空间或空间。粒子每时刻的状态对应此空间的一个点。若粒子的自由度为,则空间为维。而在系统理论中,我们用全部个粒子的坐标和动量张开一个维的空间,叫空间。整个系统每时刻的状态都在空间中对应一个点。
对于经典的情形,由于空间的动量和坐标是连续的,所以微观态数是不可数的。为了计算微观态数,习惯把相空间划分成格子,每个自由度对应的两个相格边长和的乘积规定为一个常数。当足够小时,代表一个状态所占体积。换句话说,一个相格就是一个微观态,某体积元内有多少个相格,就代表有多少个微观态。
对于量子体系,由于能级本身是分立的,一个能级能容纳的微观态数就是相应的简并度。
只要找到了粒子在相应空间中的分布,那么后面的任务就是寻找它的宏观热力学规律了。所以分布规律的获得是统计物理的核心任务。
那么,我们有哪些方法来获得这个分布呢?
大量粒子构成的系统各有不同,有的体系内,粒子相互之间的作用很弱,而有的比较强;有的系统是孤立的,有的是封闭的,还有的是完全开放的。
研究发现,对那些力学规律相同,且相互作用很弱的粒子组成的系统,主要采用一类叫做最概然统计的方法。根据其粒子所满足的力学规律的类型,这类方法又分为三种具体方法,分别是麦克斯韦-玻尔兹曼(M-B)统计、玻色-爱因斯坦(B-E)统计和费米-狄拉克(F-D)统计,分别适用于经典粒子、玻色子和费米子构成的体系。
对于经典粒子,它们遵循牛顿力学,所以每个粒子的运动是有确定的轨道,因此是可分辨的。而非经典当然就是量子粒子,它们是用波函数描述的,没有轨道,所以它们是不可分辨的。量子粒子又按照自旋是整数或半整数分别叫玻色子和费米子。与玻色子不同,费米子受泡利不相容原理的约束。
需要指出的是,对于某些定域的量子粒子构成的体系,粒子的波函数几乎不会发生交叠,粒子也可分辨,也可采用M-B统计来研究。所以M-B统计既可以是经典统计,也可以是量子统计,取决于粒子的种类。
不过,最概然统计法只适用于近独立的粒子系统。对那些粒子之间存在不同作用的一般系统,可采用吉布斯发明的系综统计法来处理,根据系统分属孤立,封闭和开放三种情况,有微正则,正则和巨正则三种系综统计法。
下面以M-B分布为例,说说最概然分布。
M-B分布适合可分辨的近独立粒子系统,这里以量子体系为例说明。
粒子处在一系列能级上,设第个能级的简并度为,即该能级上有个量子态,设落在第个能级上的粒子有个,那么的表达式就代表分布了。
前面讲玻尔兹曼熵的时候,给出了将全部粒子放入若干个间隔的方法数,即现在相比而言,多了一步,因为第个能级有个量子态可供选择,个粒子放进去,有的次方种方法。而考虑全部能级,共有方法数为根据乘法原理,总的方法数为根据最概然分布的要求,微观态数达到最大,必然有。根据,借助斯特林近似,同时考虑到两个约束条件
利用拉格朗日乘子法计算得最终分布为对于经典的M-B分布,相空间体积元对应此处的能级,所以只要把能级简并度替换为体积元容纳的状态数即可。设粒子自由度为,一个状态所占体积——相格体积为,则
对于B-E分布和F-D分布,经过类似的套路,可得到它们的分布分别为这里面的和就是拉格朗日乘子,分别满足其中为玻尔兹曼常数,为化学势。玻尔兹曼常数没什么好说的,至于什么是化学势,读者自己去了解下吧。
得到分布之后,我们就可据此来获取各种不同体系的热力学量和它们的方程。其中的一个重要的量是(巨)配分函数,例如,对经典M-B统计,它被定义为
通过它可求得内能和熵,进而可得到其他的量和关系式。在此不再赘述。
总之,你会发现,统计物理不仅与已有的热力学体系完美契合,而且能带来更多的新认识。
27
从理想气体到光子气体
前面提到,麦克斯韦速度分布律只是M-B分布的一个特例,下面来看看,具体是怎么回事。
理想气体分子之间除了碰撞的瞬间之外,没有相互作用,并且理想气体分子是可分辨的,所以理想气体显然是服从经典的M-B统计的。
理想气体的分子平动动能为考察空间中体积内,并且动量在内的状态数为根据M-B分布,相空间体积元内拥有的分子数为气体总分子数为,则把代入积分得将此式再代入得将动量换成速度得将积分则得上式两边同时除以,用表示分子数密度,则得单位体积内,速度位于~内的分子数为按照随机变量的概率密度函数的定义(见“随机事件与概率”部分第2式),定义归一化的速度分布函数因此,速度分布函数为如果按照统计物理的习惯,分布函数应表示粒子个数,所以习惯将上式再乘以后再定义为分子按速度的分布,那么它就不是归一化的。
看到了吧,麦克斯韦速度分布的确就是M-B分布的特例。
正如前面提到的,不同的温度对应的曲线不同,根据速度的某个统计量(例如最概然速率)可得到温度。
除了气体之外,还有很多其他粒子系统,例如光子气和金属内的电子气,它们都是全同粒子体系,分别服从B-E分布和F-D分布。
下面就来简单的聊聊光子气吧。
光子气,简单的说,就是平衡态辐射场的量子化,典型的就是黑体辐射。1900年10月19日,德国物理学家马克斯·普朗克(Max Planck,1858—1947)提交了他发现的黑体辐射公式,它的形式如下其中表示温度为的黑体在角频率附近单位角频率间隔内的辐射出射度。

马克斯·普朗克
为了解释这个公式,普朗克在1900年12月14日正式提出了量子论,开启了人类研究量子力学的奇妙之旅。
普朗克当年是利用内插法,在维恩和瑞利发现的公式的基础上得到普朗克公式的。
现在有了量子统计方法,只要按照B-E分布,考虑三维自由粒子的驻波条件,便可推得普朗克公式。
根据B-E分布,由于光子数不守恒,故,所以光子在确定的能级上的光子数为其中为简并度,也就是能级包含的量子态数目,这个可按如下方法得到。
根据量子力学,空间三个维度上的长度都应与自由粒子的波长满足倍数关系,根据光子波长与动量的关系,就有将三式微分并相乘(想想,为什么是相乘?)得考虑到光子的两个自旋方向,最终的量子态这就是上式的两倍。所以光场空间内,动量在~内的量子态数为
其实这个结果可以换一个角度来得到。根据前面空间的知识,与经典粒子类似,在相空间体积元内能容纳多少个量子态?
提示:不是容纳多少个光子,是容纳多少个量子态!因为相空间是状态空间,不是粒子的坐标空间。量子态数其实就是方法数,当然按乘法原理来求嘛,这就是上面那个问题的答案。
根据不确定关系,动量和坐标的不确定度的乘积约为,也就是说,相空间的相格的边长为。而光子是三维粒子,因此相格的体积为,同样考虑到自旋,故得该体积元所容纳的量子态数即为上式。
所以,能量为的光子数为采用球坐标表示即将角度积分,并根据和得每个光子的能量为,故得总能量为这就是普朗克公式。
若用波长为变量,则普朗克公式变为下图是按波长为自变量画出的能谱曲线。
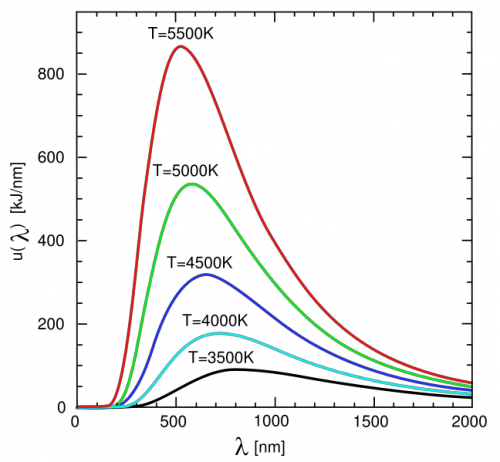
由图可知,随着温度升高时,黑体辐射能量最集中那个部分的光的波长越小,那么温度与峰值波长之间仅仅是负相关还是成反比呢?
英国物理学家维恩发现了这个关系是反比关系,即其中为常数,约等于2.897×10-3m·K。此即维恩位移定律,据此规律,只要知道某个黑体辐射的峰值波长,就可以知道它的温度。
例如,太阳表面的温度就可据此得到,因为地球上测得的太阳光峰值波长为510nm,据此计算太阳表面的温度为宇宙微波背景辐射是宇宙爆炸留下的“余音”,它是一种遍布在宇宙中的各向同性的微弱的电磁辐射,经过测量发现其峰值波长为1.063mm,计算得其温度约为2.73K 。
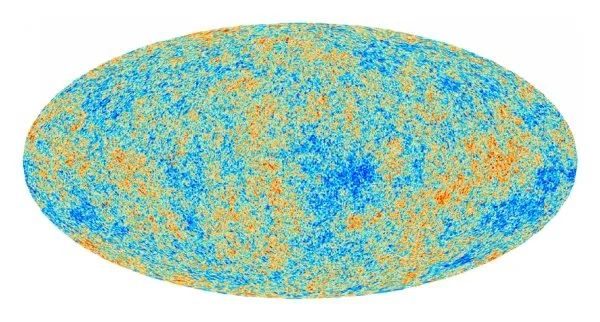
现在明白了,虽然宇宙广袤的空间中物质如此稀薄,甚至光子走100亿年都没机会碰到别的粒子,但就是这样空空如也的近乎完美真空,依然存在温度。
其实,广袤的宇宙中中除了光子之外,还有大量的中微子,它是一种费米子,利用F-D统计方法分析会发现,中微子也会产生一个约为1.95K的背景温度,具体细节在此不再赘述。
对大多数人来说,温度的微观或统计意义是指:大量粒子作无规则热运动的平均动能。然而此刻,在不经意间,温度的含义来了一个华丽转身——温度不再是粒子热运动的动能,因为很显然,光子的速度都是光速嘛!
对于光子等非物质分子的粒子来说,温度只是作为熵的微分定义式中的分母,也就是上述关于温度的统计定义中所说的——温度是等容过程中内能对熵的变化率!
所以,温度是一种纯粹的统计量,它不一定与粒子的运动直接关联。
那么问题就来了,你可能就会怀疑:这种温度与原来我们熟悉的那种热运动的温度是统一的吗?
想想,热力学的温度是如何引入的?
不错,是通过热力学第零定律以“热平衡的标志”的标志的名义引入的。
不管温度可以换成什么方式定义和理解,都会与这个最初的定义一致。换句话说,温度永远都是热平衡的标志。
是不是感觉微波背景辐射的温度无法体现为热平衡的标志?
你错了!一样的!当你在那遥远的宇宙的某个空旷的地方放上一支温度计时,它最终也会给出大约2.73K的度数。无论你把什么东西放在那里,包括你自己,最后都会达到大约2.73K的温度。
那么,这一切是如何发生的呢?简单的说,是因为电磁波与物质之间的电磁相互作用所导致的。你完全可以想象很多小球——它们就是光子,不断地与物质中地分子发生碰撞,最后一起达到了平衡——拥有同样地温度。
不过,若某种粒子几乎不与其他粒子发生作用,例如中微子,它不与光子作用,换句话说,它们之间本来就没有热接触!自然也无法达到热平衡。因此,中微子背景辐射会造成另一个独立的温度。
所以,万变不离其宗,温度还是那个温度!
那么问题又来了,既然如此,把温度定义为等容过程中内能对熵的变化率到底有何必要性呢?难道就为了换一个角度理解一下?
非也非也!这会带来更大的惊喜!它就是负温度。
28
什么是负温度?
众所周知,摄氏温标下有负数温度,一般称零下温度。但此处“负温度”是另有所指,它是指绝对温度下的负数温度值。
呃?奇怪了,根据热力学第三定律,绝对零度都不可能达到,那怎么还会有负温度呢?
让我们把目光再次聚焦到温度的统计表达式由该式可知,温度之所以总是正数,盖因内能相对熵是正相关的,即当体系的微观态数增加时,能量总是增加的。
但是,这个难道是必须的吗?有没有随着混乱度增加,能量反而下降的系统呢?如果有的话,那温度不就得用负数表示吗?
先来看一个例子。
设想有一栋高楼,一群人依次从1楼开始往上参观,每个人的进度不同,但最后大家必须到顶层集合。
如果只考虑这些人的重力势能,他们一开始出发时势能是最小的,此后势能一直增加到最大。
但在这个过程中,人的混乱度并不是递增的。一开始他们都在1楼时,混乱度最小;中间过程他们的位置比较乱,混乱度就比较大;到最后,他们又集中在顶层时混乱度又回到最小。
很显然,势能随混乱度的变化不是单调的。
这个例子中有一个不合理的条件——只考虑了势能,实际中的系统的能量应该考虑总能。但通过这个例子可以发现,要使能量随熵的变化不是单调的,体系的能级数必须有限,正如这里的楼层数有限。
所以类似的,若某个粒子系统的能级数有限,且最高能级有上界,则其能量和熵会在不同时刻取最大值,那么它们之间的关系就不是单调的。
一开始时,所有的粒子都在基态,能量最低,状态数为,熵为0。此后粒子开始从外界吸收能量。
随着粒子不断被激发到更高能级,系统开始变得混乱。当所有的能级上都拥有相同(或近似)数目的粒子时,粒子的混乱度达到最大,熵取最大值,此时温度达到无限大——为什么?后面马上就来!
随着系统继续不断从外界吸收能量,开始有粒子不断被激发到更高的能级,但混乱度必然减小,直到所有的粒子都被激发到最高能级,系统的混乱度与基态时相同,熵也为零,但能量达到最大。
下图为能量与熵的关系示例,只有两个能级,能级间隔为,粒子总数为。由于玻尔兹曼常数很小,图中熵的表达式取为。
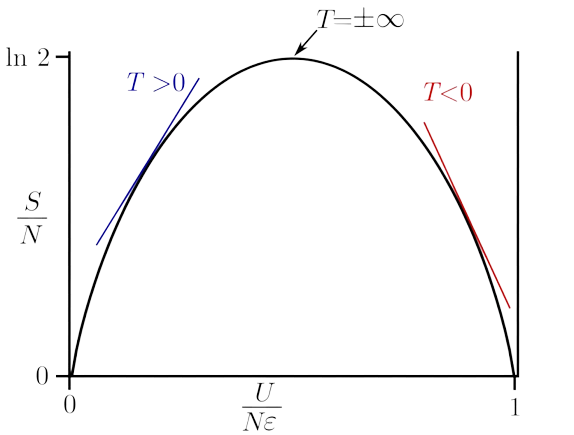
由图可见,内能随熵增加的过程中,切线斜率为正,体系具有正温度;而当熵达到最大值之后,内能再增加时熵必然减小,切线斜率为负,体系具有负温度。
前面提到,当所有的粒子都均匀的分布在各个能级上时,体系温度为无穷大,可能你觉得有点不可思议吧?
根据M-B分布,两个能级和上面的粒子数之比为若粒子按能级均匀分布,则上式等于1,而只有当指数为0时才能使非零数的幂为1,所以要想粒子按能级均匀分布,必须但由于,要想上式趋于零,只有让趋于正无穷或负无穷。
既然正无穷和负无穷温度下,粒子按能级的分布完全相同,那说明它们所导致的那个统计量——温度,是一样的。换句话说,正温度中的正无穷和负温度中的负无穷是相同的温度。
由此还可看出,负温度比任何正温度——包括正无穷大温度还要高!
为什么呢?
一种最偷懒的解释是:既然负温度是负数,那么绝对值越小,温度当然越高嘛!所以任意负温度数值都比负无穷大温度要高,那么自然也就比任何正温度都要高!
但若按此道理,正无穷大温度与负无穷大温度不可能相等啊!
真正可靠的依据是热力学第二定律。
在系统从正温度状态变到负温度状态的过程中,能量不断增加,所以一个负温度状态比正温度状态能量高。当正负温度系统相互接触时,热必然从负温度系统传到正温度系统。
而根据热力学第二定律的克劳修饰表述,热只会自动的从高温物体传到低温物体。
所以负温度比任何正温度,包括正无穷大温度都要高!
如果把温度的数值排个顺序的话,那就是正无穷和负无穷是相同的温度,假设有两个结构完全相同的系统分别处于+0K和-0K,那么它们接触后将达到共同的热平衡温度K。
那么,负温度的-0与正温度的+0是相同的吗?
非也!它们代表不同的状态,+0代表能量最低的状态,而-0代表能量最高的状态。加热负温度系统与降温正温度系统同样困难,所以这两个温度都是不可能达到的,此即考虑负温度后的热力学第三定律。
讲了这么多,你可能会问:实际中存在负温度吗?如果没有,那上面这些岂不是纸上谈兵嘛?
实际情况是,负温度已经从实验上实现了!早在1951年,科学家就发现核自旋体系可以处于绝对温度为负的态上。
讲到这里,有人会感到很困惑:比无穷大温度高的负温度都能达到,那传说中的温度极限——普朗克温度又是个什么东东?
是啊,难道普朗克温度比-0温度还要高不成,要不然怎么称之为极限温度?
非也非也!
提出这个问题的人,完全忘了前面提到的负温度存在的前提!
负温度是针对某个具有能量上限的系统来说的,这个能量上限值本身可以很小,所以负温度并不意味着巨大的能量,它本质上只代表一种粒子数分布的反转——能量高的能级粒子数反而多。
而普朗克温度只是量子力学给出的一个温度的理论上限,是一个很大但有限的值,凡是超出这个值的温度在现有的物理理论中是没有意义的。
所以,负温度虽然数值上比普朗克温度大,但实际所代表的能量完全没有可比性。
最后,来说说温度的数值问题。
诸位是不是觉得绝对温度的数值关系有点怪怪的?数值的大小与温度的高低竟然不是一致的,这不符合一般的数学习惯啊!
并且,诸君发现没有,既然负温度可以达到,那么正负无穷也可以达到,但正的零和负的零K反而不能达到,这也让人感觉不自然。
有没有办法改变这种情况呢?
当然有办法!有人曾提出一种温度,其定义如下按照此式,绝对温度的对应温度的,而绝对温度的+0和-0分别对应温度的和。
这样一来,对应于绝对温度的奇葩顺序+0→±∞→-0,这种温度给出的顺序为:-∞→±0→+∞。
根据这种温度,正温度比负温度高,而且正无穷和负无穷温度都无法达到,这样就完全符合数学习惯了!更重要的是,采用这种温度,原来的物理规律并没有任何变化。
29
写在最后
行文至此,温度一事大概也聊得差不多了,再不控制一下的话,都要成书了。
先总结一下温度概念吧。
温度,一般人理解为表示物体冷热程度的物理量。热力学第零定律将其定义为系统达到热平衡的标志。
温标主要有经验温标、理想气体温标和绝对温标,它们是一致的,但只有绝对温标才是完全独立于物质性质的。
在理想气体模型下,温度反映大量分子作无规则热运动的剧烈程度。在学习了熵的概念之后,温度被定义为等容过程中内能对熵的变化率,描述系统能量的无序化的程度。
温度不限于物质分子体系,对任何粒子系统,由于粒子按能量分布,必然导致温度这个统计量。
能级数有限且最高能级有上界的系统会导致负温度,负温度是比正无穷大温度都要高的温度。
不知你理解得如何呢?
本文主要是为那些初学大学物理或对大学物理感兴趣的中学生而写的。如果你对热力学和统计力学比较熟悉,阅读这篇文章可能不会有什么新收获。因为文章所讲的内容都是非常常规的基础物理知识,并未涉及什么高深的难题。
其实这篇文章很早就开始写,一开始只是想写写对温度的理解,但后来发现牵扯的东西越来越多,于是就干脆以温度为主线,把整个热学串起来讲了一遍。
当然,还有很多内容没有涉及,这是没有办法的事,毕竟热学还有统计力学的内容岂是用一篇文章就能讲得了的!
一直觉得热力学与统计物理的逻辑和理论体系非常美妙,但又感觉理解不到位。这次基于自己的理解,用较为通俗的大白话将其中与温度有关的部分连贯的写出来,也算是践行费曼学习法,巩固和加深一下对热学的理解。
必须承认的是,为了把一些问题讲清楚,自己不得不反复学习和深入思考,在这个过程中发现自己以往理解上的欠缺,收获也挺大的。
编辑:黄飞
-
热力学
+关注
关注
0文章
43浏览量
9313 -
麦克斯韦
+关注
关注
0文章
19浏览量
5732
原文标题:什么是温度?什么是负温度?
文章出处:【微信号:bdtdsj,微信公众号:中科院半导体所】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
晶圆表面各部分的名称
数控铣床由哪些部分组成的?各部分有什么关系
并联电路总功率与各部分功率的关系
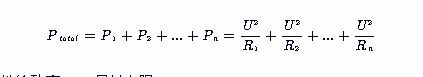




 浅谈热学背后的逻辑结构和各部分的关系
浅谈热学背后的逻辑结构和各部分的关系













评论