神经网络在ADC误差校正中的应用

“使用由 MATLAB 和 Deep Learning Toolbox 设计和训练的神经网络来对 ADC 误差进行后校正后，在 ASIC 上实现时，恩智浦设计的神经网络所需的面积只有 ADC 的 15%，正常工况下的功耗是 ADC 的大约 1/16。”

以集成电路 (IC) 形式实现的模数转换器 (ADC) 容易因 IC 制造缺陷而产生误差。

晶体管、电阻和电容等interwetten与威廉的赔率体系 元件失配会导致信号失真，如导致严重的总谐波失真 (THD)。

减少 ADC 误差的一种方法是使用更大的模拟元件来增强设计。

这种方法通过提高匹配来降低失真系数，但需要更多面积和功耗。

第二种方法是增加校准电路，但这也需要额外的芯片面积，增加了成本和功耗，而且，这通常还要求了解待校准误差的确切成因。

在恩智浦半导体埃因霍温总部，我和同事使用由 MATLAB 和 Deep Learning Toolbox 设计和训练的神经网络来对 ADC 误差进行后校正。

在 ASIC 上实现时，该网络所需的面积只有 ADC 的 15%，正常工况下的功耗是 ADC 的大约 1/16。

设计和训练神经网络

我们在实验室中向 30 个 ADC 样本(裸片)输入参考信号并捕获数字输出，从而生成训练数据。我们另外留出 10 个样本用于验证网络。

由于 ADC 误差同时受温度和电压的影响，我们在九种不同的电压与温度组合下测试每个样本，总共获得 360 个测量值。

我们使用信号处理方法对数据进行预处理，然后使用测得的 ADC 数字输出值作为神经网络的输入。我们将校正后的输出信号与原始参考信号进行比较，据此更新网络系数(图 1)。

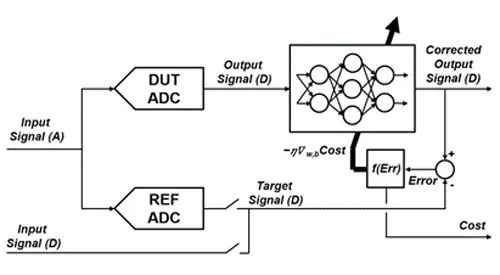
图 1.神经网络训练设置。

项目刚开始的时候，我没怎么用过神经网络，因此不确定网络该有多复杂。

最初，我在 MATLAB 中创建了基本的两层和三层网络，并在各层尝试不同的神经元数量。第一层和第二层的神经元使用 sigmoid 激活函数，输出层激活函数则是线性的。使用的代价函数是最小均方 (LMS) 代价函数。

我们基于手头的数据集和上述早期配置训练网络，发现可以加入电压和温度测量值作为预测变量来提高网络性能。经过这一更改，网络在各种温度和电压条件下的性能都有显著提升。

计算 IC 面积和功耗

现在，这个神经网络能够有效地后校正 ADC 误差，那下一步就是计算它需要多少芯片面积和功耗。

为此，我从 MATLAB 生成了经过训练的神经网络的 Simulink 模型。

接下来，我使用 Fixed-Point Designer 量化所有网络系数，然后使用 HDL Coder 从网络生成 VHDL 代码。

我的同事通过 HDL Verifier 协同仿真在 Simulink 中验证生成的 VHDL，然后使用 Cadence Genus 来综合设计。

他还在 Cadence 平台上使用 28 纳米 CMOS 制程进行物理实现，生成功耗报告，并计算使用的栅极数量和这些栅极所需的面积。

分析结果表明，使用神经网络校正 ADC 误差，面积和功耗成本都相对较低。

要实现一个能将信噪比提高约 17 dB 的网络，只需 4600 多个栅极，占据 0.0084 平方毫米的芯片面积。ADC 的面积是 0.06 平方毫米，是网络的七倍多。当处于活动状态时，网络功耗大约 15 µW，而 ADC 功耗为 233 µW。

作为误差校正电路，这样的面积和功耗估计值可以说是过关了，但我相信，我们还可以通过优化改进这些数字。即便我在机器学习方面经验尚浅，但用 VHDL 实现网络的这个工作流并不复杂。

因此，虽然我是新手，但相比传统方法，我也并没有多花太多时间，就设计和实现了基于神经网络的电路。

提高可重用性和可移植性

近期，我们计划在几个方向进行探索，验证神经网络在 ADC 误差校正中的应用。

首先，我们希望更好地了解经过训练的网络是如何执行误差校正的，以便将生产环境下出现意外行为的风险降至最低。

其次，我们想扩展我们的数据集。我们需要知道，如果使用 100 万个而不是仅仅 40 个样本，之前的结果是否依然成立。

最后，我们想衡量神经网络的可重用性。我们预计，相比传统设计，这一网络能够更有效地补偿各种 ADC 上的不同误差，因为网络能够适应各种各样的传递函数。

不过，我们需要进一步的测试来验证此假设。

原文标题：MATLAB 芯思路 | 用神经网络对 ADC 误差进行后校正

文章出处：【微信公众号：MATLAB】欢迎添加关注!文章转载请注明出处。

审核编辑：汤梓红