简介
支持向量机基本上是最好的有监督学习算法了。最开始接触SVM是去年暑假的时候,老师要求交《统计学习理论》的报告,那时去网上下了一份入门教程,里面讲的很通俗,当时只是大致了解了一些相关概念。
这次斯坦福提供的学习材料,让我重新学习了一些SVM知识。我看很多正统的讲法都是从VC 维理论和结构风险最小原理出发,然后引出SVM什么的,还有些资料上来就讲分类超平面什么的。
这份材料从前几节讲的logistic回归出发,引出了SVM,既揭示了模型间的联系,也让人觉得过渡更自然。
重新审视logistic回归
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。
因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
形式化表示就是
假设函数
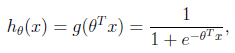
其中x是n维特征向量,函数g就是logistic函数。
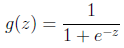 的图像是
的图像是
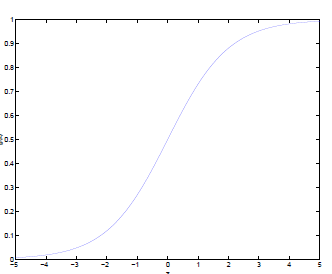
可以看到,将无穷映射到了(0,1)。
而假设函数就是特征属于y=1的概率。
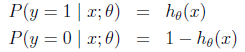
当我们要判别一个新来的特征属于哪个类时,只需求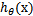 ,若大于0.5就是y=1的类,反之属于y=0类。
,若大于0.5就是y=1的类,反之属于y=0类。
再审视一下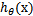 ,发现
,发现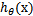 只和
只和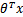 有关,
有关,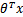 >0,那么
>0,那么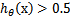 ,g(z)只不过是用来映射,真实的类别决定权还在
,g(z)只不过是用来映射,真实的类别决定权还在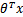 。还有当
。还有当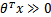 时,
时,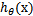 =1,反之
=1,反之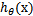 =0。
=0。
如果我们只从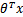 出发,希望模型达到的目标无非就是让训练数据中y=1的特征
出发,希望模型达到的目标无非就是让训练数据中y=1的特征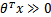 ,而是y=0的特征
,而是y=0的特征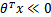 。
。
Logistic回归就是要学习得到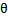 ,使得正例的特征远大于0,负例的特征远小于0,强调在全部训练实例上达到这个目标。
,使得正例的特征远大于0,负例的特征远小于0,强调在全部训练实例上达到这个目标。
图形化表示如下:
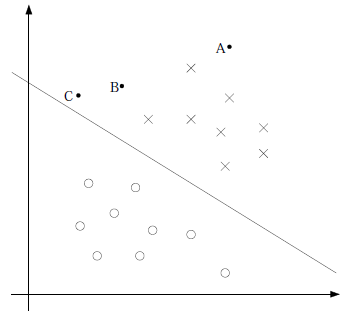
中间那条线是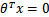 ,logistic回顾强调所有点尽可能地远离中间那条线。学习出的结果也就中间那条线。
,logistic回顾强调所有点尽可能地远离中间那条线。学习出的结果也就中间那条线。
考虑上面3个点A、B和C。从图中我们可以确定A是×类别的,然而C我们是不太确定的,B还算能够确定。这样我们可以得出结论,我们更应该关心靠近中间分割线的点,让他们尽可能地远离中间线,而不是在所有点上达到最优。
因为那样的话,要使得一部分点靠近中间线来换取另外一部分点更加远离中间线。我想这就是支持向量机的思路和logistic回归的不同点,一个考虑局部(不关心已经确定远离的点),一个考虑全局(已经远离的点可能通过调整中间线使其能够更加远离)。这是我的个人直观理解。
形式化表示
我们这次使用的结果标签是y=-1,y=1,替换在logistic回归中使用的y=0和y=1。同时将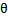 替换成w和b。
替换成w和b。
以前的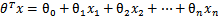 ,其中认为
,其中认为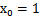 。现在我们替换
。现在我们替换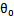 为b,后面替换
为b,后面替换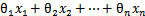 为
为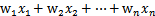 (即
(即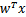 )。这样,我们让
)。这样,我们让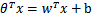 ,进一步
,进一步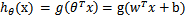 。
。
也就是说除了y由y=0变为y=-1,只是标记不同外,与logistic回归的形式化表示没区别。再明确下假设函数
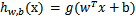
上一节提到过我们只需考虑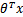 的正负问题,而不用关心g(z),因此我们这里将g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系如下:
的正负问题,而不用关心g(z),因此我们这里将g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系如下:
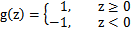
函数间隔(functional margin)和几何间隔(geometric margin)
给定一个训练样本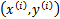 ,x是特征,y是结果标签。i表示第i个样本。我们定义函数间隔如下:
,x是特征,y是结果标签。i表示第i个样本。我们定义函数间隔如下:
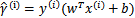
可想而知,当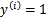 时,在我们的g(z)定义中,
时,在我们的g(z)定义中,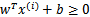 ,
,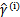 的值实际上就是
的值实际上就是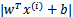 。反之亦然。
。反之亦然。
为了使函数间隔最大(更大的信心确定该例是正例还是反例),当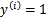 时,
时,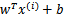 应该是个大正数,反之是个大负数。因此函数间隔代表了我们认为特征是正例还是反例的确信度。
应该是个大正数,反之是个大负数。因此函数间隔代表了我们认为特征是正例还是反例的确信度。
继续考虑w和b,如果同时加大w和b,比如在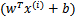 前面乘个系数比如2,那么所有点的函数间隔都会增大二倍,这个对求解问题来说不应该有影响,因为我们要求解的是
前面乘个系数比如2,那么所有点的函数间隔都会增大二倍,这个对求解问题来说不应该有影响,因为我们要求解的是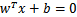 ,同时扩大w和b对结果是无影响的。
,同时扩大w和b对结果是无影响的。
这样,我们为了限制w和b,可能需要加入归一化条件,毕竟求解的目标是确定唯一一个w和b,而不是多组线性相关的向量。这个归一化一会再考虑。
刚刚我们定义的函数间隔是针对某一个样本的,现在我们定义全局样本上的函数间隔
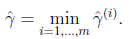
说白了就是在训练样本上分类正例和负例确信度最小那个函数间隔。
接下来定义几何间隔
假设我们有了B点所在的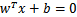 分割面。任何其他一点,比如A到该面的距离以
分割面。任何其他一点,比如A到该面的距离以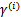 表示,假设B就是A在分割面上的投影。
表示,假设B就是A在分割面上的投影。
我们知道向量BA的方向是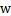 (分割面的梯度),单位向量是
(分割面的梯度),单位向量是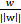 。A点是
。A点是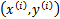 ,所以B点是x=
,所以B点是x=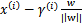 (利用初中的几何知识),带入
(利用初中的几何知识),带入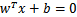 得,
得,
进一步得到
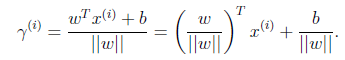
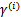 实际上就是点到平面距离。
实际上就是点到平面距离。
再换种更加优雅的写法:
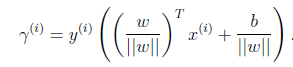
当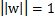 时,不就是函数间隔吗?是的,前面提到的函数间隔归一化结果就是几何间隔。
时,不就是函数间隔吗?是的,前面提到的函数间隔归一化结果就是几何间隔。
他们为什么会一样呢?因为函数间隔是我们定义的,在定义的时候就有几何间隔的色彩。同样,同时扩大w和b,w扩大几倍,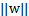 就扩大几倍,结果无影响。同样定义全局的几何间隔
就扩大几倍,结果无影响。同样定义全局的几何间隔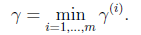
最优间隔分类器(optimal margin classifier)
回想前面我们提到我们的目标是寻找一个超平面,使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面,我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。
形象的说,我们将上面的图看作是一张纸,我们要找一条折线,按照这条折线折叠后,离折线最近的点的间距比其他折线都要大。形式化表示为:
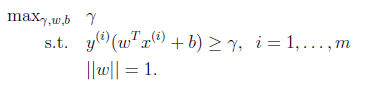
这里用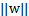 =1规约w,使得
=1规约w,使得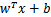 是几何间隔。
是几何间隔。
到此,我们已经将模型定义出来了。如果求得了w和b,那么来一个特征x,我们就能够分类了,称为最优间隔分类器。接下的问题就是如何求解w和b的问题了。
由于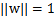 不是凸函数,我们想先处理转化一下,考虑几何间隔和函数间隔的关系,
不是凸函数,我们想先处理转化一下,考虑几何间隔和函数间隔的关系,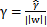 ,我们改写一下上面的式子:
,我们改写一下上面的式子:
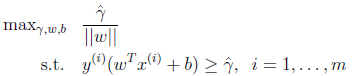
这时候其实我们求的最大值仍然是几何间隔,只不过此时的w不受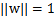 的约束了。然而这个时候目标函数仍然不是凸函数,没法直接代入优化软件里计算。我们还要改写。
的约束了。然而这个时候目标函数仍然不是凸函数,没法直接代入优化软件里计算。我们还要改写。
前面说到同时扩大w和b对结果没有影响,但我们最后要求的仍然是w和b的确定值,不是他们的一组倍数值,因此,我们需要对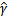 做一些限制,以保证我们解是唯一的。
做一些限制,以保证我们解是唯一的。
这里为了简便我们取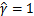 。这样的意义是将全局的函数间隔定义为1,也即是将离超平面最近的点的距离定义为
。这样的意义是将全局的函数间隔定义为1,也即是将离超平面最近的点的距离定义为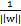 。由于求
。由于求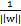 的最大值相当于求
的最大值相当于求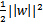 的最小值,因此改写后结果为:
的最小值,因此改写后结果为:
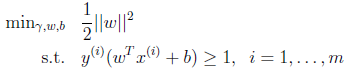
这下好了,只有线性约束了,而且是个典型的二次规划问题(目标函数是自变量的二次函数)。代入优化软件可解。
到这里发现,这个讲义虽然没有像其他讲义一样先画好图,画好分类超平面,在图上标示出间隔那么直观,但每一步推导有理有据,依靠思路的流畅性来推导出目标函数和约束。
—版权声明—
仅用于学术分享,版权属于原作者。
若有侵权,请联系 删除或修改!
转自:JerryLead
http://www.cnblogs.com/jerrylead/archive/2011/03/13/1982639.html
编辑:jq
-
算法
+关注
关注
23文章
4610浏览量
92860 -
向量机
+关注
关注
0文章
166浏览量
20875 -
SVM
+关注
关注
0文章
154浏览量
32454
原文标题:优雅的读懂支持向量机 SVM 算法
文章出处:【微信号:gh_f39db674fbfd,微信公众号:尖刀视】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
计算机视觉威廉希尔官方网站 的AI算法模型
机器学习算法原理详解
一文带你读懂什么是工控机

如何利用一些小技巧实现SVM的增量式训练




 一文带你快速读懂支持向量机 SVM 算法
一文带你快速读懂支持向量机 SVM 算法













评论