简述System Generator的ECC加解密系统的设计

椭圆曲线密码系统（ECC）与其他公钥加密系统相比，因其密钥长度短、安全强度高等诸多优点，被公认为最有前途的公钥密码体系，受到人们的普遍关注和研究［1-4］。

在国内外有关ECC的研究方面，主要集中在 ECC的时间复杂度和空间复杂度上［2-4］。参考文献［2］研究模逆和标乘的快速算法，参考文献［3］针对KP算法将改进的Booth算法嵌入传统算法，极大地降低了迭代次数和有限域运算量。参考文献［4］将所有的模运算全转化为模乘运算和模加运算，并改进了LSD乘法器，利用该单元进行模运算，从而其硬件实现了具有面积小、速度快等优点。

目前国内的密码威廉希尔官方网站 还是落后于国外，特别是在生活应用中，国内的企业基本上是引用国外的密码威廉希尔官方网站 进行二次开发。如果要将实现的椭圆曲线密码系统应用到实际中，则需要通过系统集成芯片设计（SOC），将FPGA上实现的椭圆曲线密码系统集成实用性的加密芯片。一旦设计过程中所需的资源和条件不够完善，将导致加密芯片的制作难以实现。为此，本文借助Xilinx公司提供的强大的系统级硬件仿真工具System Generator［5］，研究并设计ECC加解密系统。

1 椭圆曲线密码体制

由于最终是要在硬件上实现椭圆曲线密码体制［6］，所以本文选择的有限域是特征为2的GF（2n），选择的椭圆曲线方程如式（1）所示。

可见椭圆曲线密码体制涉及到GF（2n）上的模加运算、模乘运算、求逆运算，还有椭圆曲线的KP点乘运算，下面对几个主要算法进行分析。

1.1 GF（2n）域上的模乘运算

模乘模块是整个设计中最关键的模块，模乘的过程包括多项式相乘和取模两个过程。传统的乘法器是将两个m位操作数相乘，然后对其进行f（x）求模。这样的缺点就是需要一个2m位的寄存器来存储中间结果，势必会浪费资源。本文采用全串行移位相加法来实现模乘运算［6］。该算法只有简单的移位和“异或”运算，但是需要大量的移位运算，如果A、B具有m位，则需要进行m-1次移位运算，这是比较耗时的。

但是本文使用的FPGA工作在61.44 MHz时钟下，m一般取值在200左右，因此全串行移位相加法大概需要的是ns级的时间，而且全串行移位算法也是最节省资源的算法。通过Modelsim仿真该模块，得到图1所示结果。其中， clk是系统时钟61.44 MHz；reset是系统复位信号；en是使能端口；din是乘数输入端口，低位在前；dout是输出结果；rdy是输出结果有效指示。

1.2 GF（2n）域上的模逆运算

对于GF（2n）域上的模逆运算，当今最有效的算法就是扩展欧几里德算法和基于费马定理的模逆算法。扩展欧几里德算法用时会比基于费马定理的模逆算法用时短很多，但是相应地是以牺牲硬件资源为代价，在后面的点乘算法和最后的椭圆曲线密码体制的实现耗用资源很大。

扩展欧几里德算法还要去另外设计一个多项式模块，而基于费马定理的模逆算法只需要反复调用先前做好的模乘模块就行，再加上本文用的FPGA时钟频率本身就高，因此本文选择费马定理来做模逆算法。通过Modelsim仿真该模块，得到图2所示结果。其中，clk是系统时钟61.44 MHz；reset是系统复位信号；en是模逆使能；din是输入数据；a_inv是输出结果；rdy是输出结果有效指示。

选取参数：

K=157E51751D89C66CBDF44596BF7F653876A18C4B12

40B85A;

x=36B3DAF8A23206F9C4F299D7B21A9C369137F2C84

AE1AA0D;

y=7658E73433B3F95E332932E70EA245CA2418EA0EF9

8018FB;

b=2E45EF571F00786F67B0081B9495A3D95462F5DE0A

A185EC;

f=800000000000000000000000000000000000000000000

201。

仿真结果：

Cx=34EEC5768673E71B8CDC139FB8EB4ACD9989FAA

E1EC9EF1D;

Cy=779097F490A2DA7A6B09A9518733B4817D5C21947

547D2A1。

2 System Generator搭建ECC加密系统

System Generator是业内领先的高级系统级FPGA开发工具。其作用是借助FPGA设计高性能DSP系统并和Simulink实现无缝链接，快速建模并自动生成代码［5］。System Generator最大的特点就是可利用Simulink建模和仿真环境来实现FPGA设计，无需了解和使用RTL级硬件语言，让DSP设计者能够发挥基于FPGA的DSP的最大性能和灵活性，并缩短整个设计周期。

前文用FPGA实现了ECC的各个关键模块，下面用先前生成的各个模块代码通过System Generator的黑盒子生成各自相应的模块。再将这些模块搭建成完整的ECC模块，以便在Matlab工作空间中输入相应的参数、明文和相应的使能端口就可以实现加密；输入相应的参数、密文和相应的使能端口就可以实现解密。但是本文所涉及的参数较大，输入的过程很耗费时间，因此本文将参数都固定在一个ROM中间，只要控制相应的使能信号，就可以达到一个加解密的interwetten与威廉的赔率体系 过程。

2.1数据输入模块的搭建

本文中的端口有使能端口和参数端口，其中，使能端口是1 bit的，就可以用计数器来实现。对于191个bit位的参数，可先将其分解成6组的32 bit系数， 存在如图4所示的ROM中，只要改变ROM中的值就可以控制输入参数的值，改变3个常数模块就可以控制参数输入的时刻。

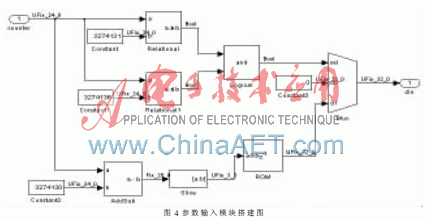
2.2 ECC系统的搭建与仿真结果

利用代码生成的KP模块、求逆模块和乘法模块搭建成ECC加解密系统。由于ECC加解密系统的各个子模块有很多的反馈端口，搭建起来的图显得比较乱，因此可以在ECC系统中的m文件添加 this block.addFile（）。把各个子模块添加到ECC顶层模块中，这样就相当于把各个子模块集成在统一的黑盒子中。

设置运行时间为4 000 000个时钟周期，将加解密指示信号设置为加密，点击运行，进行加密仿真，在工作区间可以看到，明文输入和对应的密文输出。例如，当输入的明文为“4129534493046158328227537522838960054530294419451055575666”时，输出的密文为“3625519732263338515328819742424233936313311718087”。

设置运行时间为4 000 000个时钟周期，将加解密指示信号设置为解密，点击运行，进行解密仿真，在工作区间可以看到密文输入和对应的的明文输出。例如，当输入的密文为“362551973226333851532881974242423393631

3311718087”， 则输出的明文为“4129534493046158328227537522838960054530294419451055575666”。

ECC模块加解密运算输出有效数据的时钟周期是第3274550，使能信号则是在第11个时钟周期输入，因此整个运算过程中数据的输入输出所耗费的时间是3274550-11=3 274 539个时钟周期，所以对于采用时钟频率为61.44 MHz的FPGA来说，只要用3 274 539/61.44 ？滋s就可以完成一次加密算法，或者一次解密算法。总共用的时间为3274539/61.44 ns=53.3 ms，而若单单只用Matlab仿真运行，大概需要时间为20 min。因此采用硬件实现椭圆曲线密码系统的优越性不言而喻。

参考文献

［1］ HANKERSON D，MENEZES A， VANSTONE S． Guide to elliptic curve cryptography［M］． Springer Verlag New York Inc，2004：25-147.

［2］ MA S W， HAO Y L， PAN Z Q． Fast implementation for modular inversion an d scalar multiplication in the elliptic curve cryptography［C］.IITA ’08，Beijing，China，2008:488-492.

［3］ 龚书，刘文江，戎蒙恬。一种椭圆曲线密码加密算法及实现［J］。高威廉希尔官方网站 通讯，2004（3）：25-28.

［4］ 唐薛峰，沈海斌，严晓浪.GF（2^m）上椭圆密码体制的硬件实现［J］。计算机工程与应用，2004，40（11）：96-98.

［5］ 田耕，徐文波，胡彬.Xilinx ISE Design Suite 10.x FPGA开发指南［M］。北京：人民邮电出版社，2008.

［6］ 祝跃飞，张亚娟。椭圆曲线公钥密码导引［M］。 北京：科学出版社，2006.

编辑：jq