一、图像旋转原理
图像旋转是指图像按照某个位置转动一定角度的过程,旋转中图像仍保持这原始尺寸。图像旋转后图像的水平对称轴、垂直对称轴及中心坐标原点都可能会发生变换,因此需要对图像旋转中的坐标进行相应转换。
如图,原图像经过顺时针旋转角度为 θ 后,源图像的坐标为 P0 ( Xo, Yo ) 的点移动到了 P1(X1, Y1)。
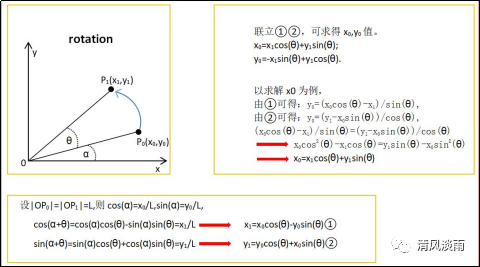
经过推导,可以得到上述的 P0 和P1 的坐标变换关系式。
方案一、【正向预设】从原图映射到目标图像在此方案中,实现代码的方式是正向的思路,将原图中的像素点的坐标进行坐标的旋转,然后直接幅值到输出的图像中,此方案旨在找到输入坐标与输出坐标之间的代数对应关系。
在该方法中,首先将原始坐标以及目标坐标放入了极坐标中,并且通过在极坐标中的关系,找到了同时满足X0,Y0,X1,Y1四个参量的方程组,以此来解出对应的坐标关系,并以此为基础得到了输入与输出之间的矩阵运算关系如下:
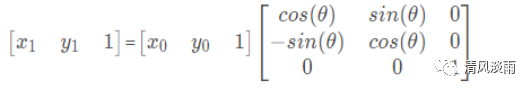
Matlab代码实现如下:
clear allclc
% 读入图片im = imread(‘1.jpg’);figure;imshow(im);
% 求出旋转矩阵a = 40 / 180 * pi;R = [cos(a), -sin(a); sin(a), cos(a)];
% 求出图片大小 ch为通道数 h为高度 w为宽度sz = size(im);h = sz(1);w = sz(2);ch = sz(3);c = [h; w] / 2;
% 初始化结果图像im2 = uint8(zeros(h, w, 3));
for k = 1:ch for i = 1:h for j = 1:w p = [i; j]; % round为四舍五入 pp = round(R*(p-c)+c); if (pp(1) 》= 1 && pp(1) 《= h && pp(2) 》= 1 && pp(2) 《= w) im2(pp(1), pp(2), k) = im(i, j, k); end end endend
% 显示图像figure;imshow(im2);
但在实际的测试中发现,这种方法所旋转得到的图像有着较为严重的失真现象,具体情况如下图所示:
原图
旋转后的图像
很明显可以看到,在旋转之后这两张图片出现了较大的差别,首先是原图像被裁减了,其次是目标图像中有较多的瑕点(杂点)。究其原因在于,从原图旋转后得到的目标图像的像素位置在原图中找不到。另外就是边缘被裁剪的问题,由于在这个方案中约束了显示区域,因此在旋转的过程中,部分像素点就会由于超出边界而被裁剪。针对以上的两个问题,进行了如下改进。
方案二、【逆向预设】从目标图像映射到原图
由于在之前的方案中出现了杂点以及图像边缘裁剪的问题,因此在本方案中,我们采用了逆向思维,用目标图像的坐标去与原图的坐标进行坐标匹配,若在原图像中能找到匹配的图像,就显示该点旋转后的点坐标,若在原图中找不到该点,则不显示该点,通过这样就解决了杂点的问题。 其中,pp为旋转在后的坐标对应矩阵,在if语句中限定了原图的区域,用此区域则可以到原图中的坐标点,以此来排除不在区域中的坐标点,这样就可以解决杂点的问题。
在这种方案下,坐标的对应关系如下:
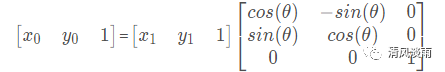
MATLAB仿真代码如下:
clear allclc
% 读入图片im = imread(‘1.jpg’);figure;imshow(im);
% 求出旋转矩阵a = 20 / 180 * pi;R = [cos(a), sin(a); -sin(a), cos(a)];
% 求出图片大小 ch为通道数 h为高度 w为宽度
sz = size(im);h = sz(1);w = sz(2);ch = sz(3);c = [w;h] /2;
% 初始化结果图像im2 = uint8(zeros(h, w, 3));for k = 1:ch %遍历输出图像所有位置的像素 for i = 1:h for j = 1:w p = [j; i]; % p :输出图像的像素坐标 % round为四舍五入 pp = round(R*(p-c)+c); %pp :对应到输入图像的像素坐标 %逆向进行像素的查找 if (pp(1) 》= 1 && pp(1) 《= w && pp(2) 》= 1 && pp(2) 《= h) im2(i, j, k) = im(pp(2), pp(1), k); end end endend
% 显示图像figure;imshow(im2);
这样,该旋转后的图像就有了较好的还原度,达到了相应的题目要求,具体的方案的效果如下图所示:
原图
旋转后的图像
如图所示,相对方案一而言,图像的效果就好了很多,但图像边缘仍然存在边缘被切割的现象。 方案三:考虑到未对旋转后的图像进行显示区域的划分,因此此类旋转只是对单一像素点的旋转,然后在原图像的显示区域上进行坐标点的重新组合,得到显示的图像。在解决的方法的思路上,采用目标显示区域的重新划分来解决该问题。
具体思路是,采用原图像的长宽作为基准,再用坐标转换的关系,将长和宽转换到旋转后的坐标系中,得到目标图像在旋转后坐标系中的显示区域,代码具体如下:
% 读入图片im = imread(‘1.jpg’);
figure;imshow(im);
% 求出旋转矩阵a = 30 / 180 * pi;R = [cos(a), -sin(a); sin(a), cos(a)];R = R‘; % 求出旋转矩阵的逆矩阵进行逆向查找
% 计算原图大小sz = size(im);h = sz(1);w = sz(2);ch = sz(3);c1 = [h; w] / 2;
% 计算显示完整图像需要的画布大小hh = floor(w*sin(a)+h*cos(a))+1;ww = floor(w*cos(a)+h*sin(a))+1;c2 = [hh; ww] / 2;
% 初始化目标画布im2 = uint8(ones(hh, ww, 3)*128);for k = 1:ch for i = 1:hh for j = 1:ww p = [i; j]; pp = (R*(p-c2)+c1); mn = floor(pp); ab = pp - mn; a = ab(1); b = ab(2); m = mn(1); n = mn(2); % 线性插值方法 if (pp(1) 》= 2 && pp(1) 《= h-1 && pp(2) 》= 2 && pp(2) 《= w-1) im2(i, j, k) = (1-a)*(1-b)*im(m, n, k) + a*(1-b)*im(m+1, n, k)。.. + (1-a)*b*im(m, n, k) + a*b*im(m, n, k); end end endend
% 显示图像figure;imshow(im2);
这样,就解决了图像边缘被裁剪的问题,是整个图像得以完整的显示,实际的效果如下:
原图
旋转后的图像
从图示的效果可以看出,边缘区域被裁剪的问题被解决了,但问题是图片加阴影的区域面积比原图大很多。 综合以上三种方案,结合实际需求,由于我们的显示是在一块固定大小的屏幕上进行显示,整个图像的显示范围有限,采用CORDIC算法进行坐标变换产生的延时太大。最终基于处理速度和资源占用的均衡考虑,最终选择方案二作为我们图像旋转的设计方案。
三、旋转坐标计算
在该设计中,要求图像拥有0到360的任意角度的旋转,坐标变换需要角度的正弦和余弦值。 利用matlab生成正余弦表,并将其扩大256倍,打印到文件中。利用得到的正余弦表数值,将其写入verilog代码中,生成正余弦查找表。通过输入角度值来索引其正余弦数值。Matlab生成正余弦列表的代码如下:

该正弦,余弦通过MATLAB计算得到,并预先储存到FPGA的片上储存空间中,在进行坐标变换时,读取对应角度的正弦,余弦值,进行坐标变换。由于计算得到的正弦和余弦值为浮点数,而FPGA擅长于进行整数运算。故要进行浮点数到整数的转换,具体的实现方法是,将计算得到的浮点正弦,余弦值乘上 256 后再取整,计算得到的结果于原结果相比被扩大了256倍,而在数字电路中,除法操作可以用移位来进行。结果右移8位即等效于除于256 。 坐标变换的核心代码如下:

将坐标变换计算模块封装为一个子模块,输入输出图像的坐标和旋转角度后,即可计算出对应的输入图像对应的像素的坐标。然后读取该坐标的像素值,写入到旋转重建的图像对应的坐标位置即可。
四、效果展示(Results show)
0、原图 (正常显示)
1、顺时针旋转22度
2、顺时针旋转90度
3、顺时针旋转270度
4、顺时针旋转341度
五、说明
在公众号对话框回复 FPGA2019 ,即可获得该项目的工程源代码,详细的文档说明,MATLAB仿真代码。
编辑:lyn
-
FPGA
+关注
关注
1629文章
21748浏览量
603964 -
MATLAB仿真
+关注
关注
4文章
176浏览量
19943 -
图像旋转
+关注
关注
0文章
3浏览量
2204
原文标题:基于FPGA的图像旋转系统设计
文章出处:【微信号:HXSLH1010101010,微信公众号:FPGA威廉希尔官方网站 江湖】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
基于FPGA实现图像直方图设计
FPGA 实时信号处理应用 FPGA在图像处理中的优势
FPGA在图像处理领域的优势有哪些?
基于 FPGA 的会议系统设计
基于FPGA的CCD工业相机系统设计
基于FPGA的图像采集与显示系统设计
基于FPGA的实时边缘检测系统设计,Sobel图像边缘检测,FPGA图像处理
旋转花键的使用注意事项!

RFID血液智能流转系统在赤峰市中心血站正式启动




 详解基于FPGA的图像旋转系统的运用
详解基于FPGA的图像旋转系统的运用













评论