1 永磁同步电机在dq坐标系上的数学模型(为什么要解耦)
将三相静止坐标系下的PMSM的数学模型经过CLARK 和 PARK 变换之后,得到以下dq坐标系上的数学模型。

如果将这个数学模型转换为一张图来表示,就会很清楚的看到其中的耦合关系。
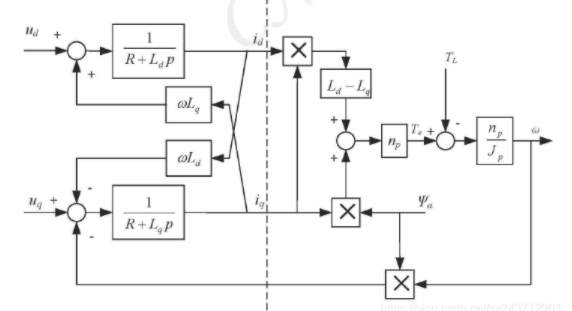
由永磁同步电机的电压方程和数学模型可以看出,d轴电压 Ud 不仅受 d轴电流 id 的影响,还受q轴电流 iq的影响,这说明永磁同步电机 d轴电压 和 q轴电压 存在一种耦合关系。我们可以将公式中的 和 视作耦合项,由于耦合项的影响,我们的Ud 和 Uq 是无法实现独立控制的。我们必须想办法解决这个问题。
另外是实际控制中,这种耦合会对控制器的性能产生比较大的危害,从公式里面可以看出 转速 的值越大这个耦合项就越大,这说明电机的速度越高,这个耦合项对电机的控制器性能的影响就越大,这是非常严重的,我们必须要消除它。
2 解耦的策略 (怎么解耦)
此文章中我只介绍一种简单的解耦策略,
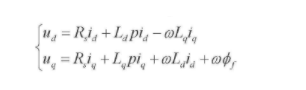
从公式上可以看出,永磁同步电机耦合的影响是可以通过id=0的控制策略和前馈补偿的方式抵消掉的,总而言之,只要消除
ud 表达式后面 iq 的影响 和 uq 表达式后面 id 的影响,就可以达到解耦的目的。
2.1 id=0的控制策略对解耦的贡献
首先我们讨论 id=0 对解耦的作用,矢量控制 id =0 控制的本质是实现 dq轴的电流静态解耦,
d轴的阻尼绕组是会产生磁通的,与永磁体的磁通共同构成电机的磁场。id变化的同时,总的磁通变化,这是一层耦合关系。
id=0 时,磁通完全由永磁体来提供。直轴的电流为0,这就使得电机没有直轴的电枢反应,即直轴是不贡献转矩的。电机的所有的电流全部用来产生电磁转矩,这与一台他励直流电动机就等效,只用控制 iq 的值就可以控制电机的转矩了,这就很自然的实现了电机的静态解耦。
当 id =0 后,电机的电压方程
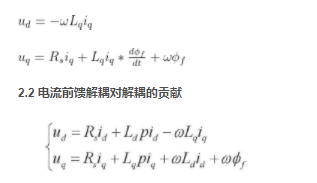
2.2 电流前馈解耦对解耦的贡献
永磁同步电机耦合的影响可以通过前馈补偿的方式抵消掉,在d轴控制器和q轴控制器的输出端,分别引入与永磁同步电机dq轴电压方程中耦合项相等的信号作为耦合补偿,即可实现电流控制器的解耦控制。因此也成为电压前馈解耦。解耦的控制框图如图所示。
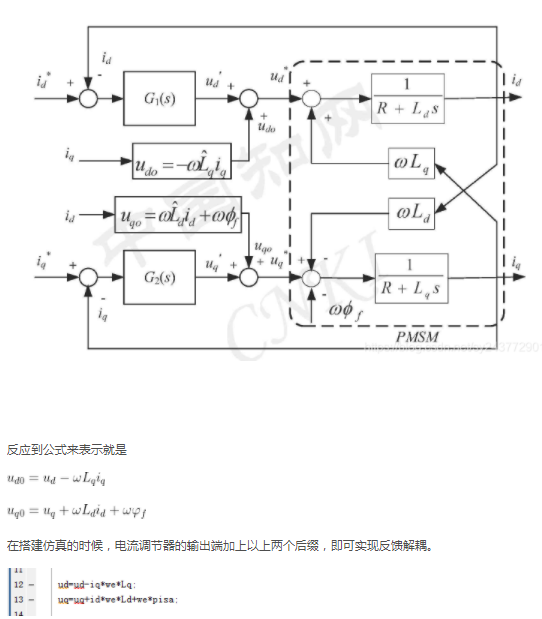
我自己是通过编程来实现的。
3 实验结果对比
3.1 id=0 控制仿真实验结果(下左为转速波形和 iq 的波形,右为 id 的波形)
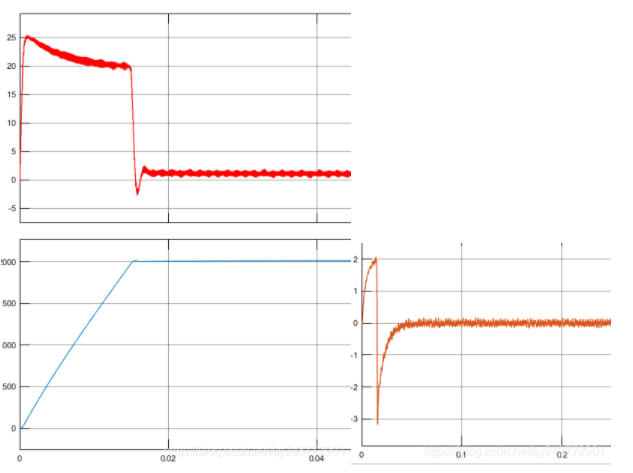
3.2 电流反馈解耦控制仿真结果(下左为转速波形和 iq 的波形,右为 id 的波形)
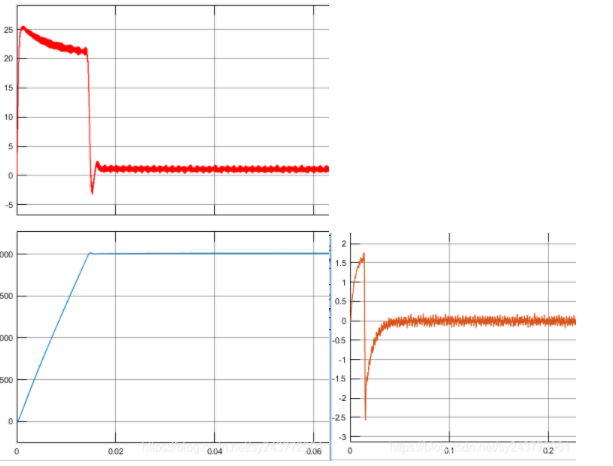
3 波形具体分析
3.1 iq波形解耦前后对比(左为解耦前 iq波形,后解耦后 iq波形)
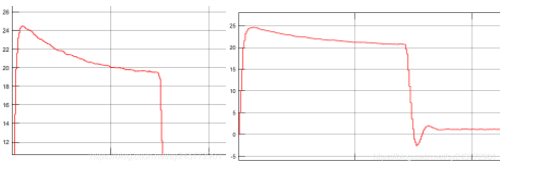
对比前后 iq 的波形,明显解耦后的 iq 比解耦前的相应速度要快,且平稳度要更好,这将意味着电磁转矩也更加稳定,所以电机的阶跃响应的速度提升。此次仿真的电机是一台隐极的电机,如果是凸极的电机效果将更明显。
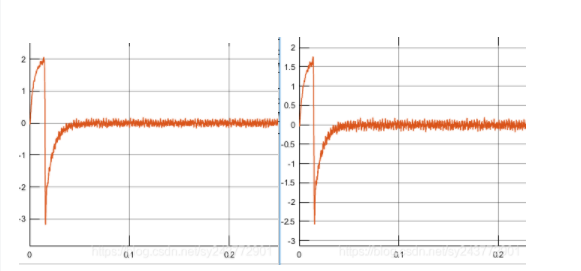
3.1 id波形解耦前后对比(左为解耦前 id波形,后解耦后 id波形)
对比前后 id 的波形可以看出,在电机启动阶段,id 的幅值明显得到了反馈的校正,幅值明显比解耦前要小,解耦后最大值才0.5安,尤其在高速时,这种效果将更加明显。(此处这个尖峰还未弄清楚原因,如有了解的可以在下面留言,感谢感谢)
小结
永磁同步电机在运行过程中,交直轴电压之间存在耦合的现象,即d轴的参数变化会引起q轴的参数变化,这将不利于我们的控制。而电流前馈解耦就是从电机模型出发,使电压在经过PI控制器整定之后的输出,得到一个跟耦合量相同的前馈补偿,补偿可以将耦合项抵消,从而实现了解耦。
从实验的效果来看,解耦后的电机阶跃响应的速度更快,且电流的波形更加稳定,这将有益于整个系统的性能。
编辑:hfy
-
电机控制
+关注
关注
3534文章
1876浏览量
268779 -
永磁同步电机
+关注
关注
28文章
873浏览量
49543 -
解耦
+关注
关注
0文章
40浏览量
11896
发布评论请先 登录
相关推荐




 永磁同步电机控制系列的数学模型(7):怎么解耦
永磁同步电机控制系列的数学模型(7):怎么解耦










评论