logistic回归是一种广义的线性回归,通过构造回归函数,利用机器学习来实现分类或者预测。
原理
上一文简单介绍了线性回归,与逻辑回归的原理是类似的。
预测函数(h)。该函数就是分类函数,用来预测输入数据的判断结果。过程非常关键,需要预测函数的“大概形式”, 比如是线性还是非线性的。 本文参考机器学习实战的相应部分,看一下数据集。
// 两个特征
-0.017612 14.053064 0
-1.395634 4.662541 1
-0.752157 6.538620 0
-1.322371 7.152853 0
0.423363 11.054677 0
0.406704 7.067335 1
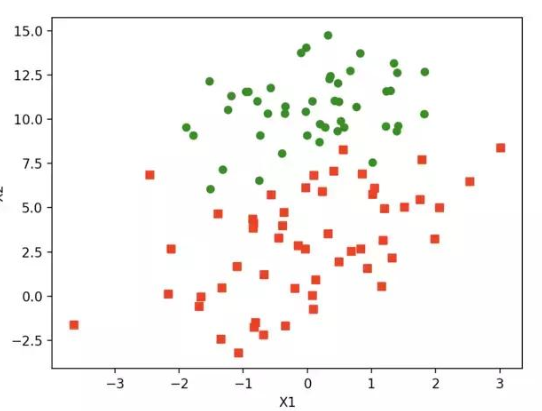
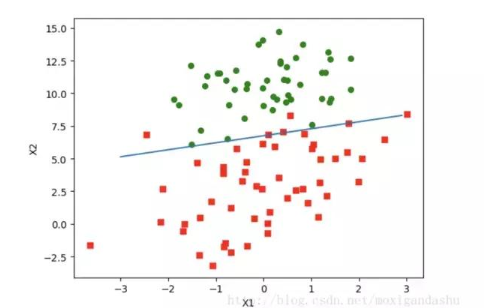
如上图,红绿代表两种不同的分类。可以预测分类函数大概是一条直线。Cost函数(损失函数):该函数预测的输出h和训练数据类别y之间的偏差,(h-y)或者其他形式。综合考虑所有训练数据的cost, 将其求和或者求平均,极为J函数, 表示所有训练数据预测值和实际值的偏差。
显然,J函数的值越小,表示预测的函数越准确(即h函数越准确),因此需要找到J函数的最小值。有时需要用到梯度下降。
具体过程
构造预测函数
逻辑回归名为回归,实际为分类,用于两分类问题。 这里直接给出sigmoid函数。
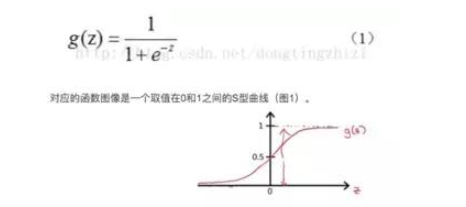
接下来确定分类的边界,上面有提到,该数据集需要一个线性的边界。 不同数据需要不同的边界。
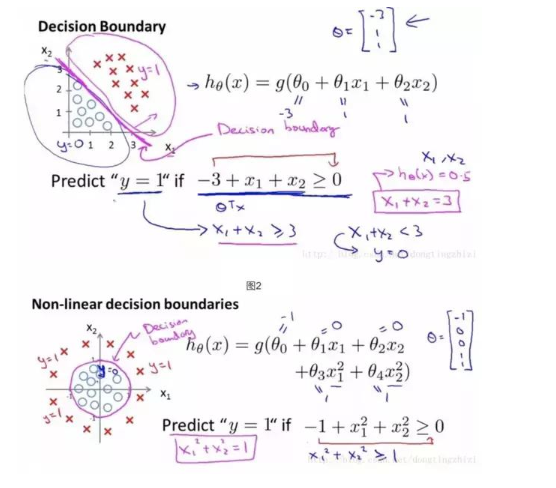
确定了分类函数,将其输入记做z ,那么
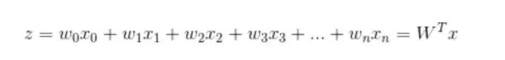
向量x是特征变量, 是输入数据。此数据有两个特征,可以表示为z = w0x0 + w1x1 + w2x2。w0是常数项,需要构造x0等于1(见后面代码)。 向量W是回归系数特征,T表示为列向量。 之后就是确定最佳回归系数w(w0, w1, w2)。cost函数
综合以上,预测函数为:
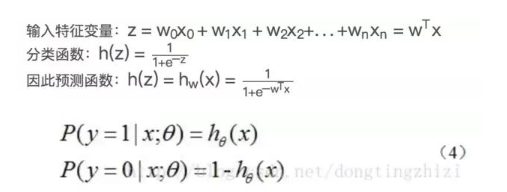
这里不做推导,可以参考文章 Logistic回归总结
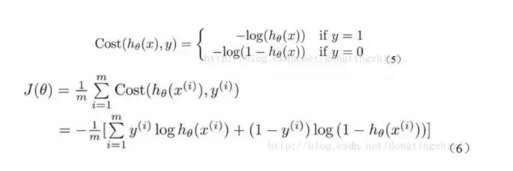
有了上述的cost函数,可以使用梯度上升法求函数J的最小值。推导见上述链接。
综上:梯度更新公式如下:

接下来是python代码实现:
# sigmoid函数和初始化数据
def sigmoid(z):
return 1 / (1 + np.exp(-z))
def init_data():
data = np.loadtxt(‘data.csv’)
dataMatIn = data[:, 0:-1]
classLabels = data[:, -1]
dataMatIn = np.insert(dataMatIn, 0, 1, axis=1) #特征数据集,添加1是构造常数项x0
return dataMatIn, classLabels
复制代码
// 梯度上升
def grad_descent(dataMatIn, classLabels):
dataMatrix = np.mat(dataMatIn) #(m,n)
labelMat = np.mat(classLabels).transpose()
m, n = np.shape(dataMatrix)
weights = np.ones((n, 1)) #初始化回归系数(n, 1)
alpha = 0.001 #步长
maxCycle = 500 #最大循环次数
for i in range(maxCycle):
h = sigmoid(dataMatrix * weights) #sigmoid 函数
weights = weights + alpha * dataMatrix.transpose() * (labelMat - h) #梯度
return weights
// 计算结果
if __name__ == ‘__main__’:
dataMatIn, classLabels = init_data()
r = grad_descent(dataMatIn, classLabels)
print(r)
输入如下:
[[ 4.12414349]
[ 0.48007329]
[-0.6168482 ]]
上述w就是所求的回归系数。w0 = 4.12414349, w1 = 0.4800, w2=-0.6168 之前预测的直线方程0 = w0x0 + w1x1 + w2x2, 带入回归系数,可以确定边界。 x2 = (-w0 - w1*x1) / w2
画出函数图像:
def plotBestFIt(weights):
dataMatIn, classLabels = init_data()
n = np.shape(dataMatIn)[0]
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if classLabels[i] == 1:
xcord1.append(dataMatIn[i][1])
ycord1.append(dataMatIn[i][2])
else:
xcord2.append(dataMatIn[i][1])
ycord2.append(dataMatIn[i][2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1,s=30, c=‘red’, marker=‘s’)
ax.scatter(xcord2, ycord2, s=30, c=‘green’)
x = np.arange(-3, 3, 0.1)
y = (-weights[0, 0] - weights[1, 0] * x) / weights[2, 0] #matix
ax.plot(x, y)
plt.xlabel(‘X1’)
plt.ylabel(‘X2’)
plt.show()
如下:
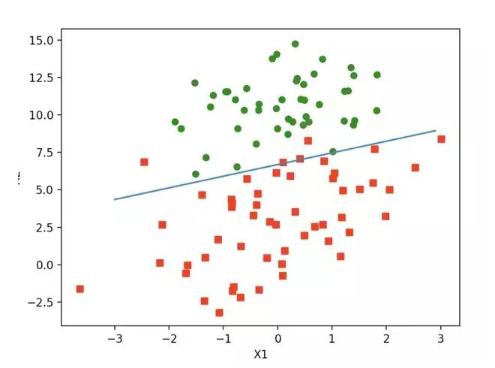
算法改进
随机梯度上升
上述算法中,每次循环矩阵都会进行m * n次乘法计算,时间复杂度是maxCycles* m * n。当数据量很大时, 时间复杂度是很大。 这里尝试使用随机梯度上升法来进行改进。 随机梯度上升法的思想是,每次只使用一个数据样本点来更新回归系数。这样就大大减小计算开销。 算法如下:
def stoc_grad_ascent(dataMatIn, classLabels):
m, n = np.shape(dataMatIn)
alpha = 0.01
weights = np.ones(n)
for i in range(m):
h = sigmoid(sum(dataMatIn[i] * weights)) #数值计算
error = classLabels[i] - h
weights = weights + alpha * error * dataMatIn[i]
return weights
进行测试:
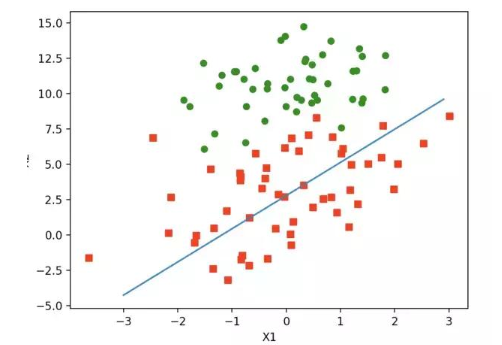
随机梯度上升的改进
def stoc_grad_ascent_one(dataMatIn, classLabels, numIter=150):
m, n = np.shape(dataMatIn)
weights = np.ones(n)
for j in range(numIter):
dataIndex = list(range(m))
for i in range(m):
alpha = 4 / (1 + i + j) + 0.01 #保证多次迭代后新数据仍然有影响力
randIndex = int(np.random.uniform(0, len(dataIndex)))
h = sigmoid(sum(dataMatIn[i] * weights)) # 数值计算
error = classLabels[i] - h
weights = weights + alpha * error * dataMatIn[i]
del(dataIndex[randIndex])
return weights
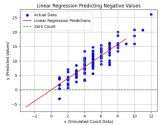
可以对上述三种情况的回归系数做个波动图。 可以发现第三种方法收敛更快。 评价算法优劣势看它是或否收敛,是否达到稳定值,收敛越快,算法越优。
总结
这里用到的梯度上升和梯度下降是一样的,都是求函数的最值, 符号需要变一下。 梯度意味着分别沿着x, y的方向移动一段距离。(cost分别对x, y)的导数。
完整代码请查看: github: logistic regression
参考文章: 机器学习之Logistic回归与Python实现
-
机器学习
+关注
关注
66文章
8408浏览量
132575 -
Logistic
+关注
关注
0文章
11浏览量
8852 -
线性回归
+关注
关注
0文章
41浏览量
4306
发布评论请先 登录
相关推荐
什么是机器学习?通过机器学习方法能解决哪些问题?

NPU与机器学习算法的关系
什么是回归测试_回归测试的测试策略
人工智能、机器学习和深度学习存在什么区别





 机器学习实战之logistic回归
机器学习实战之logistic回归











评论