“傅里叶”这个名字,我相信对很多人来说并不陌生。尤其是理工科的童鞋,对这三个字应该是如雷贯耳。
一直以来,在我们的大学专业课本中,“傅里叶”都保持着极高的出镜率。围绕这三个字的一系列名词,例如傅里叶变换、傅里叶积分、傅里叶级数,傅里叶分析等等,曾经让无数人苦不堪言、生不如死,甚至形成了长期的心理阴影。

然后,作为一位250年前的古人,至今还能在我们的教材中拥有如此重要的地位,也足以说明他的实力。
傅里叶究竟是一个什么样的人?他经历了一个怎样的人生?他的这些成就,究竟是如何取得的?
今天的文章,我们就来找寻一下答案——
傅里叶(也有译作傅立叶),全名是让·巴普蒂斯·约瑟夫·傅里叶(Baron Jean Baptiste Joseph Fourier),法国著名数学家、物理学家。
傅里叶
1768年3月21日,他生于法国中部奥塞尔的一个平民家庭,他的父亲是一个裁缝,母亲是一个普通的家庭妇女。
傅里叶的童年并不算幸福。9岁时,双亲亡故,他变成一个孤儿,被当地的一个主教收养。
1780年,他被教会送入镇上的军校就读,表现出对数学的特殊爱好。他曾经希望参加炮兵或工程兵,但因家庭地位低贫而遭到拒绝。
后来,他希望到巴黎更优越的环境中去从事数学研究。可是,法国大革命爆发,中断了他的计划。无奈之下,他于1789年回到家乡奥塞尔的母校执教。
在大革命期间,傅里叶以热心地方事务而知名,而且是一个非常有正义感的人。他替当时恐怖行为的受害者申辩,结果因此被捕入狱。出狱后,他短暂就读于巴黎师范学校,再次表现出惊人的数学才华。
1795年,当巴黎综合工科学校成立时,傅里叶被任命为助教,协助J.L.Lagrange(也就是拉格朗日,相信大家一定不会陌生)和G.Monge(蒙日,也是超级大牛),从事数学教学工作。这一年,他再次因政治原因被捕,后经同事营救获释。
拉格朗日 蒙日
1798年,蒙日选派他跟随拿破仑远征埃及。
在埃及开罗,他担任埃及研究院的秘书,并从事许多外交活动。这一期间,他仍不断地进行个人的业余研究,即数学物理方面的研究。
1801年,傅里叶回到法国。他希望继续执教于巴黎综合工科学校,但因拿破仑赏识他的行政才能,任命他为伊泽尔地区首府格勒诺布尔的高级官员。
由于政声卓著,1808年,拿破仑授予他男爵称号。
此后,几经宦海浮沉,1815年,傅里叶终于在拿破仑百日王朝的尾期辞去爵位和官职,毅然返回巴黎以图全力投入学术研究。但是,失业、贫困以及政治名声的落潮,使得傅里叶进入了一生中最艰难的时期。
好在昔日同事和学生对他施以援手,为他谋得统计局主管之职,才算维持住了生活。统计局的工作并不繁重,傅里叶得以继续从事研究。
1816年,傅里叶被提名为法国科学院的成员。一开始,路易十八因为怀疑他与拿破仑的关系,拒绝了他的提名。后来,事情得到澄清,傅里叶于1817年就职科学院,其声誉随之迅速上升。
傅里叶的任职得到了当时年事已高的 P.S.M.de Laplace(也就是拉普拉斯)的支持,却不断受到 S.D.Poisson(泊松)的反对。事实上,后来两人之间的恩恩怨怨一直就没停歇过。
拉普拉斯 泊松
1822年,傅里叶被选为科学院的终身秘书,这是极有权力的职位。
1827年,他又被选为法兰西学院院士,还被英国皇家学会选为外国会员。此时,他的个人荣誉达到了巅峰。
傅里叶一生为人正直,他曾对许多年轻的数学家和科学家给予无私的支持和真挚的鼓励,从而得到他们的忠诚爱戴,并成为他们的至交好友。
在他帮助过的科学家中,有知名的 H.C.奥斯特(Oersted)、P.G.狄利克雷(Dirichlet)、N.H.阿贝尔(Abel)和 J.C.F.斯图姆(Sturm)等人。
有一件令人遗憾的事,就是傅里叶收到伽罗瓦(Galois)的关于群论的论文时,他已病情严重而未阅,以致论文手稿失去下落。
傅里叶极度痴迷热学,他甚至认为热能包治百病。于是,在一个夏天,他关上了家中的门窗,穿上厚厚的衣服,坐在火炉边,结果,他被活活热死了。。。死了。。。了。。。
1830年5月16日,傅里叶卒于法国巴黎。
我们回顾一下傅里叶的科学成就。
他的成就主要在于他对热传导问题的研究,以及他为推进这一方面的研究所引入的数学方法。
早在远征埃及时,他就对热传导问题产生了浓厚的兴趣。后来在格勒诺布尔任职期间,他进行了大量的科学研究。
1807年,他向科学院呈交了一篇很长的论文,题为“热的传播”(Mémoire sur la propagation de la chaleur),内容是关于不连结的物质和特殊形状的连续体(矩形的、环状的、球状的、柱状的、棱柱形的)中的热扩散(即热传导)问题。在论文的审阅人中,拉普拉斯、蒙日和 S.F.拉克鲁瓦(Lacroix)都是赞成接受这篇论文的,但是拉格朗日提出了强烈的反对。
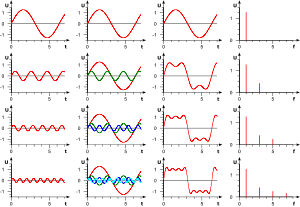
傅里叶在论文中运用正弦曲线来描述温度分布,并提出一个很有争议性的结论:任何连续周期信号可以由一组适当的正弦曲线组合而成。(这句话是不是很耳熟?高数课听过,信号与系统课听过,数字信号处理课也听过。)
但是拉格朗日坚持认为傅里叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。(不懂?放心,我也不懂 )
最终,法国科学学会屈服于拉格朗日的威望,拒绝了傅里叶的工作。不过,在审查委员会给傅里叶的回信中,还是鼓励他继续钻研,并将研究结果严密化。
究竟两位大牛谁对谁错呢?
正弦曲线无法组合成一个带有棱角的信号,这句话拉格朗日是对的。但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法不存在能量差别。基于此,傅里叶是对的。(某老师解释的,我表示继续不懂)
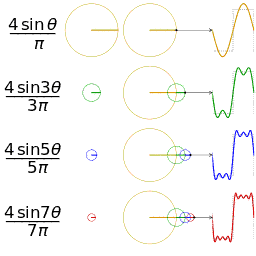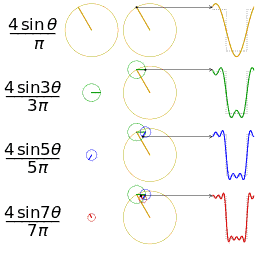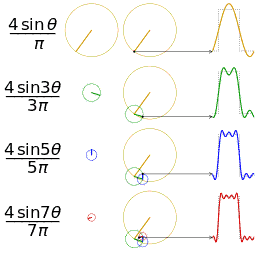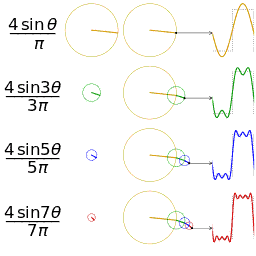
为了推动对热扩散问题的研究,科学院于1810年悬赏征求论文。傅里叶对其1807年的文章加以修改,并再次提交,题目是“热在固体中的运动理论”(Theorie du mouvement de chaleur clansles corps solides)。
这篇论文在竞争中获胜,傅里叶获得科学院颁发的奖金。但是评委——可能是由于拉格朗日的坚持——仍从文章的严格性和普遍性上给予了批评,以致这篇论文又未能正式发表。
这下子傅里叶彻底炸了。他认为这是一种无理的非难,他决心将这篇论文的数学部分扩充成为一本书(他本来还打算把物理部分出书,可惜后来没有完成)。
1822年,傅立叶终于出版了专著《热的解析理论》。
这部经典著作将欧拉、伯努利等人在一些特殊情形下应用的三角级数方法发展成内容丰富的一般理论,三角级数后来就以傅里叶的名字命名(傅里叶级数)。后来为了处理无穷区域的热传导问题又导出了“傅里叶积分”,这一切都极大地推动了偏微分方程边值问题的研究。
然而傅里叶的工作意义远不止此,它迫使人们对函数概念作修正、推广,特别是引起了对不连续函数的探讨;三角级数收敛性问题更刺激了集合论的诞生。
《热的解析理论》影响了整个19世纪分析严格化的进程,在数学史,乃至科学史上公认是一部划时代的经典性著作。
实际上,傅里叶变换远不止数学和物理学上的价值,它几乎存在于生活和科学的各个领域——研究不同的潜水器结构与水流的相互作用,试图预测即将到来的地震,识别距离遥远的星系的组成部分,寻找热量大爆炸残余物中的新物理成分,从x射线衍射模式揭示蛋白质的结构,为NASA分析数字信号,研究乐器的声学原理,改进水循环的模型,寻找脉冲星(自转的中子星),用核磁共振研究分子结构。甚至,傅里叶变换已经被用于通过破译油画中的化学物质,来识别假冒的杰克逊·波洛克绘画。
-
傅里叶
+关注
关注
0文章
59浏览量
20465
原文标题:傅里叶的坎坷人生
文章出处:【微信号:mwrfnet,微信公众号:微波射频网】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
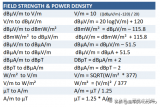
EMC常见公式大全




 傅里叶公式的由来
傅里叶公式的由来










评论