一、概述
背包问题是一类比较特殊的动态规划问题,这篇文章的侧重点会在答案的推导过程上,我们还是会使用之前提到的解动态规划问题的四个步骤来思考这类问题。
在讲述背包问题之前,首先提及一下,背包类动态规划问题和其他的动态规划问题的不同之处在于,背包类动态规划问题会选用值来作为动态规划的状态,你可以回顾下之前我们讨论过的动态规划问题,基本上都是利用数组或者是字符串的下标来表示动态规划的状态。
针对背包类问题,我们依然可以画表格来辅助我们思考问题,但是背包类问题有基本的雏形,题目特征特别明显,当你理解了这类问题的解法后,遇到类似问题基本上不需要额外的辅助就可以给出大致的解法,这也就是说,学习背包类问题是一个性价比很高的事情,理解了一个特定问题的解法,基本上一类问题都可以直接套这个解法。
二、问题雏形
首先我们来看看这样一个问题:
有 N 件物品和一个容量为 V 的背包。第 i 件物品的体积是 C[i],价值是 W[i]。求解将哪些物品装入背包可使价值总和最大。求出最大总价值
话不多说,我们还是按之前的分析四步骤来看看这个问题:
问题拆解
我们要求解的问题是 “背包能装入物品的最大价值”,这个问题的结果受到两个因素的影响,就是背包的大小,以及物品的属性(包括大小和价值)。对于物品来说,只有两种结果,放入背包以及不放入背包,这里我们用一个例子来画画表格:
假设背包的大小是 10,有 4 个物品,体积分别是 [2,3,5,7],价值分别是 [2,5,2,5]。
1、如果我们仅考虑将前一个物品放入背包,只要背包体积大于 2,此时都可以获得价值为 2 的最大价值:
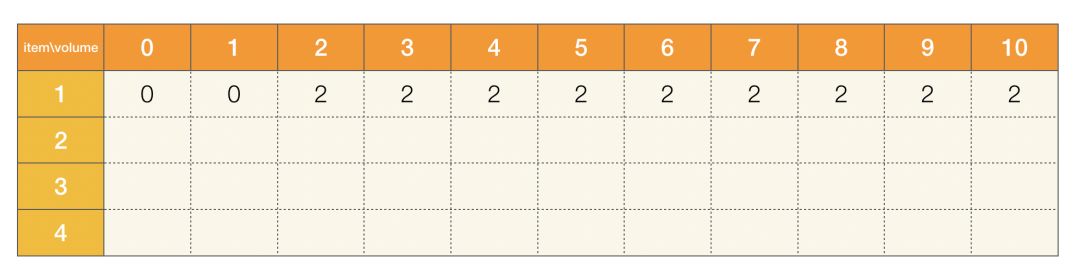
图一
2、如果我们仅考虑将前两个物品放入背包,如果背包体积大于或等于 5,表示两个物体都可放入,此时都可以获得价值为 2+5=7 的最大价值,如果不能全都放入,那就要选择体积不超,价值最大的那个:
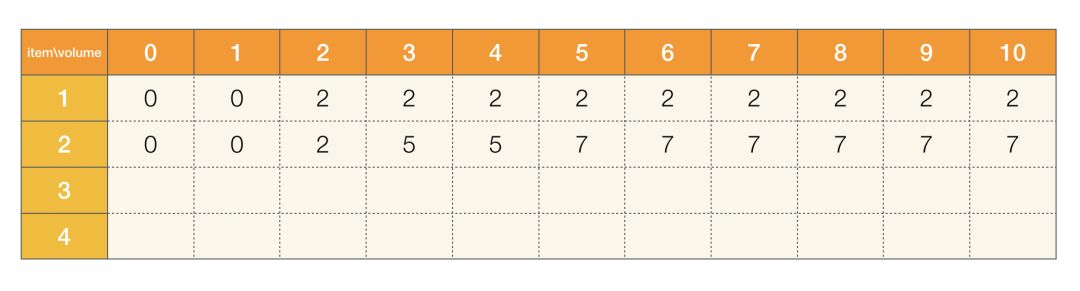
图二
3、如果我们仅考虑将前三个物品放入背包,如果背包体积大于或等于 10,表示三个物体都可放入,此时都可以获得价值为 2+5+2=9 的最大价值,如果不能全都放入,那就要选择体积不超,价值最大的那个方案:
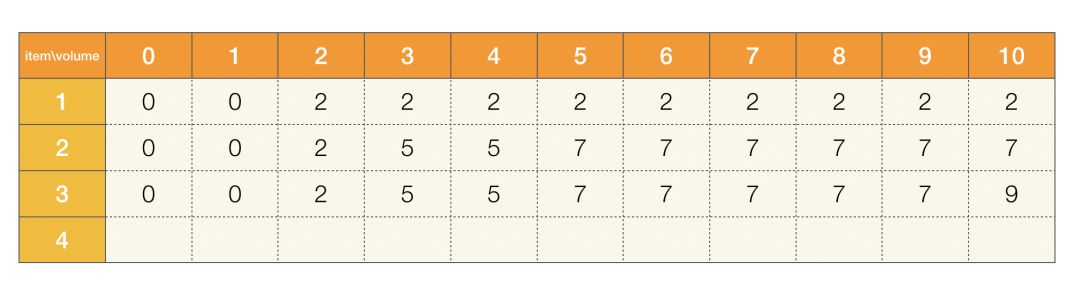
图三
4、如果我们考虑将所有物品放入背包,我们可以依据前三个物品放入的结果来制定方案:
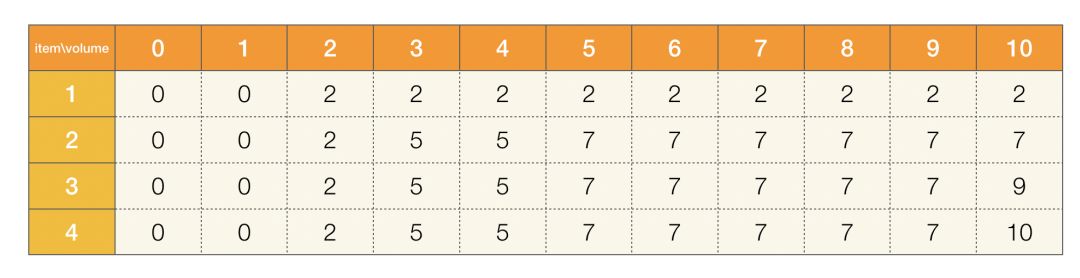
图四
这样,我们就根据物品和体积将问题拆分成子问题,也就是 “前 n 个物品在体积 V 处的最大价值” 可以由 “前 n - 1 个物品的情况” 推导得到。
状态定义
在问题拆解中,我们得知问题其实和背包的体积还有当前考虑的物品有关,因此我们可以定义dp[i][j]表示 “考虑将前 i 个物品放入体积为 j 的背包里所获得的最大价值”
递推方程
当我们考虑是否将第 i 个物品放入背包的时候,这里有两种情况
不放入,也就是不考虑第 i 个物品,那么问题就直接变成了上一个子问题,也就是考虑将 i - 1 个物品放入背包中,这样当前问题的解就是之前问题的解:
dp[i][j]=dp[i-1][j]
如果背包体积大于第 i 个物品的体积,我们可以考虑将第 i 个物品放入,这个时候我们要和之前的状态做一个比较,选取最大的方案:
dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-C[i]]+W[i])
实现
实现这一环节还是主要考虑状态数组如何初始化,你可以看到,我们每次都要考虑 i - 1,另外还要考虑背包体积为 0 的情况,因此初始化数组时多开一格可以省去不必要的麻烦
publicintzeroOnePack(intV,int[]C,int[]W){ //防止无效输入 if((V<= 0) || (C.length != W.length)) { return 0; } int n = C.length; // dp[i][j]: 对于下标为 0~i 的物品,背包容量为 j 时的最大价值 int[][] dp = new int[n + 1][V + 1]; // 背包空的情况下,价值为 0 dp[0][0] = 0; for (int i = 1; i <= n; ++i) { for (int j = 1; j <= V; ++j) { // 不选物品 i 的话,当前价值就是取到前一个物品的最大价值,也就是 dp[i - 1][j] dp[i][j] = dp[i - 1][j]; // 如果选择物品 i 使得当前价值相对不选更大,那就选取 i,更新当前最大价值 if ((j >=C[i-1])&&(dp[i][j]< dp[i - 1][j - C[i - 1]] + W[i - 1])) { dp[i][j] = dp[i - 1][j - C[i - 1]] + W[i - 1]; } } } // 返回,对于所有物品(0~N),背包容量为 V 时的最大价值 return dp[n][V]; }
这里还有一个空间上面的优化,如果你回到我们之前画的表格,考虑前 i 个问题的状态只会依赖于前 i - 1 个问题的状态,也就是dp[i][...]只会依赖于dp[i - 1][...],另外一点就是当前考虑的背包体积只会用到比其小的体积。
基于这些信息,我们状态数组的维度可以少开一维,但是遍历的方向上需要从后往前遍历,从而保证子问题需要用到的数据不被覆盖,优化版本如下:
publicintzeroOnePackOpt(intV,int[]C,int[]W){ //防止无效输入 if((V<= 0) || (C.length != W.length)) { return 0; } int n = C.length; int[] dp = new int[V + 1]; // 背包空的情况下,价值为 0 dp[0] = 0; for (int i = 0; i < n; ++i) { for (int j = V; j >=C[i];--j){ dp[j]=Math.max(dp[j],dp[j-C[i]]+W[i]); } } returndp[V]; }
这里,因为物品只能被选中 1 次,或者被选中 0 次,因此我们称这种背包问题为01 背包问题。
还有一类背包问题,物品可以被选多次或者 0 次,这类问题我们称为完全背包问题,这类背包问题和 01 背包问题很类似,略微的不同在于,在完全背包问题中,状态dp[i][j]依赖的是dp[i - 1][j]以及dp[i][k] k < j,你可以看看下面的实现代码:
publicintcompletePack(intV,int[]C,int[]W){ //防止无效输入 if(V==0||C.length!=W.length){ return0; } intn=C.length; //dp[i][j]:对于下标为0~i的物品,背包容量为j时的最大价值 int[][]dp=newint[n+1][V+1]; //背包空的情况下,价值为0 dp[0][0]=0; for(inti=1;i<= n; ++i) { for (int j = 1; j <= V; ++j) { // 不取该物品 dp[i][j] = dp[i - 1][j]; // 取该物品,但是是在考虑过或者取过该物品的基础之上(dp[i][...])取 // 0-1背包则是在还没有考虑过该物品的基础之上(dp[i - 1][...])取 if ((j >=C[i-1])&&(dp[i][j-C[i-1]]+W[i-1]>dp[i][j])){ dp[i][j]=dp[i][j-C[i-1]]+W[i-1]; } } } //返回,对于所有物品(0~N),背包容量为V时的最大价值 returndp[n][V]; }
类似的,我们还是可以对状态数组进行空间优化,依据我们之前讨论的状态之间的依赖关系,完全背包的空间优化我们直接把状态数组少开一维即可,遍历方式都不需要改变:
publicintcompletePackOpt(intV,int[]C,int[]W){ if(V==0||C.length!=W.length){ return0; } intn=C.length; int[]dp=newint[V+1]; for(inti=0;i< n; ++i) { for (int j = C[i]; j <= V; ++j) { dp[j] = Math.max(dp[j], dp[j - C[i]] + W[i]); } } return dp[V]; }
下面,我们就根据这两类背包问题,看看遇到类似的问题我们是否可以套用上面我们介绍的解法。
三、相关题目实战
LeetCode 第 416 号问题:分割等和子集。
题目来源:https://leetcode-cn.com/problems/partition-equal-subset-sum/
题目描述
给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
注意:
每个数组中的元素不会超过 100
数组的大小不会超过 200
示例 1:
输入:[1,5,11,5] 输出:true 解释:数组可以分割成[1,5,5]和[11].
示例 2:
输入:[1,2,3,5] 输出:false 解释:数组不能分割成两个元素和相等的子集.
题目分析
题目给定一个数组,问是否可以将数组拆分成两份,并且两份的值相等,这里并不是说分成两个子数组,而是分成两个子集。
直观的想法是直接遍历一遍数组,这样我们可以得到数组中所有元素的和,这个和必须是偶数,不然没法分,其实很自然地就可以想到,我们要从数组中挑出一些元素,使这些元素的和等于原数组中元素总和的一半,“从数组中找出一些元素让它们的和等于一个固定的值”,这么一个信息能否让你想到背包类动态规划呢?
如果你能想到这个地方,再配上我们之前讲的01 背包问题的解法,那么这道题目就可以直接套解法了,这里我就不具体分析了。
参考代码
publicbooleancanPartition(int[]nums){ if(nums==null||nums.length==0){ returnfalse; } intsum=0; intn=nums.length; for(inti=0;i< n; ++i) { sum += nums[i]; } if (sum % 2 != 0) { return false; } int target = sum / 2; boolean[] dp = new boolean[target + 1]; dp[0] = true; for (int i = 0; i < n; ++i) { for (int j = target; j >=nums[i];--j){ dp[j]|=dp[j-nums[i]]; } } returndp[target]; }
LeetCode 第 322 号问题:零钱兑换。
题目来源:https://leetcode-cn.com/problems/coin-change
题目描述
给定不同面额的硬币coins和一个总金额amount。编写一个函数来计算可以凑成总金额所需的最少的硬币个数。如果没有任何一种硬币组合能组成总金额,返回-1。
示例 1:
输入:coins=[1,2,5],amount=11 输出:3 解释:11=5+5+1
示例 2:
输入:coins=[2],amount=3 输出:-1
说明:
你可以认为每种硬币的数量是无限的。
题目分析
题目给定一个数组和一个整数,数组里面的值表示的是每个硬币的价值,整数表示的是一个价值,问最少选择多少个硬币能够组成这个价值,硬币可以重复选择。
虽然这里只有一个输入数组,但是我们还是可以看到背包的影子,这里的整数就可以看作是背包的体积,然后数组里面的值可以看作是物品的体积,那物品的价值呢?
在这里,你可以形象地认为每个物品的价值是 1,最后我们要求的是填满背包的最小价值,因为这里物品是可以重复选择多次的,因此可以归类于完全背包问题,套用之前的解法就可以解题,唯一要注意的一点是,这里我们不在求最大价值,而求的是最小价值,因此我们需要先将状态数组初始化成无穷大。
参考代码
publicintcoinChange(int[]coins,intamount){ int[]dp=newint[amount+1]; Arrays.fill(dp,Integer.MAX_VALUE); dp[0]=0; for(inti=0;i< coins.length; ++i) { for (int j = coins[i]; j <= amount; ++j) { if (dp[j - coins[i]] != Integer.MAX_VALUE) { dp[j] = Math.min(dp[j - coins[i]] + 1, dp[j]); } } } return dp[amount] == Integer.MAX_VALUE ? -1 : dp[amount]; }
辅助动画
LeetCode 第 518 号问题:零钱兑换II。
题目来源:https://leetcode-cn.com/problems/coin-change-2/
题目描述
给定不同面额的硬币和一个总金额。写出函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。
示例 1:
输入:amount=5,coins=[1,2,5] 输出:4 解释:有四种方式可以凑成总金额: 5=5 5=2+2+1 5=2+1+1+1 5=1+1+1+1+1
示例 2:
输入:amount=3,coins=[2] 输出:0 解释:只用面额2的硬币不能凑成总金额3。
示例 3:
输入:amount=10,coins=[10] 输出:1
注意:
你可以假设:
0 <= amount (总金额) <= 5000
1 <= coin (硬币面额) <= 5000
硬币种类不超过 500 种
结果符合 32 位符号整数
题目分析
这道题目是上一道题目的变形,题目的输入参数还是不变,变的是最后的问题,这里需要求的是 “有多少种组合方式能够填满背包”,我们还是可以套用完全背包的解法,只是最后求解的东西变了,那我们动态规划状态数组中记录的东西相应的改变即可,在这道题中,状态数组中记录组合成该价值的方案的个数即可。
参考代码
publicintchange(intamount,int[]coins){ int[]dp=newint[amount+1]; dp[0]=1; for(inti=0;i< coins.length; ++i) { for (int j = coins[i]; j <= amount; ++j) { dp[j] += dp[j - coins[i]]; } } return dp[amount]; }
K Sum。
题目描述
给定一个输入数组 array,还有两个整数 k 和 target,在数组 array 中找出 k 个元素,使得这 k 个元素相加等于 target,问有多少种组合方式,输出组合方式的个数。
注:在一种组合方式中,一个元素不能够被重复选择
题目分析
我们之前讲过 Two Sum,也提到过 3 Sum,还有 4 Sum,那这道题是否可以套用之前的解法呢?
这里有一个细节不知道你是否发现,就是这道题目仅仅是让你输出所有组合方式的个数,并没有让你输出所有的组合方式,这是决定是否使用动态规划很重要的一点。
如果没有这个 k,我相信你会很直接地想到使用01 背包问题的解法,那我们可以思考一下,基于原来的解法,如果增加了 k 这个限制,我们需要额外做些什么事情呢?
因为 k 会决定问题的状态,因此我们的状态数组中也要考虑 k,在考虑将第 k 个元素放入背包中,我们需要看的是背包中存放 k - 1 个元素的情况,这么看来,其实相比普通的01 背包问题,这道题目仅仅是增加了一维状态,没有其他的变化。
参考代码
publicintkSum(int[]array,intk,inttarget){ int[][]dp=newint[target+1][k+1]; dp[0][0]=1; for(inti=0;i< array.length; ++i) { for (int j = target; j >=array[i];--j){ //和普通01背包问题相比,仅仅是多了一层状态需要考虑 //这层状态记录的是背包里面元素的个数 //我们放入第r个元素的时候,必须确保背包里面已经有r-1个元素 for(intr=1;r<= k; ++r) { dp[j][r] += dp[j - array[i]][r - 1]; } } } return dp[target][k]; }
四、总结
背包类的动态规划问题我们就先讲到这里,我们介绍了两类比较基础的背包问题,01 背包问题和完全背包问题,解这类问题有既定的模版和思路可以参照,理解了模版问题,也就理解了一类问题,算是学习性价比很高的一类动态规划问题。
往往背包类问题可以很好地根据题目的描述判断出来,这类问题状态的定义也比较特殊,就是用值来作为动态规划的状态,我们也用了一些习题来练习了一番,相信你对背包问题有了大致的了解,也对动态规划有了更广的认识。
-
数组
+关注
关注
1文章
417浏览量
25945
原文标题:额,没想到,背包问题解题也有套路。。。
文章出处:【微信号:TheAlgorithm,微信公众号:算法与数据结构】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
使用LM75BIMX作为温度传感器检测环境温度,得到的数据持续为不符合现实的错误数据,怎么解决?
PCM2704的ROM编程好了,竟然是乱码,为什么?
欧姆定律我是很熟,只是没想到电流不按套路出牌!
Raspberry Pi CM5 还要几周才能上市吗?

评测活动第一名李工:我用Jupiter画了个原理图,然后成了段子手…

拆了某宝39.9的蓝牙音响,没想到内部电路如此丰富!

哪个STM8的开发工具最好用,最便捷?
盘点使用agv叉车的7大行业,第1个很正常,第5个是真没想到

圣同智能激光背包式激光清洗机产品介绍






 没想到,背包问题解题也有套路
没想到,背包问题解题也有套路










评论