您需要的东西
您要放入电路的东西:
一个电阻为R(在Ω中)。
输入信号(我们来自函数发生器)。
示波器(用于测试)。
从电路中得到的结果:
经过滤波的输出信号。
如何构建电路

零件在哪里?
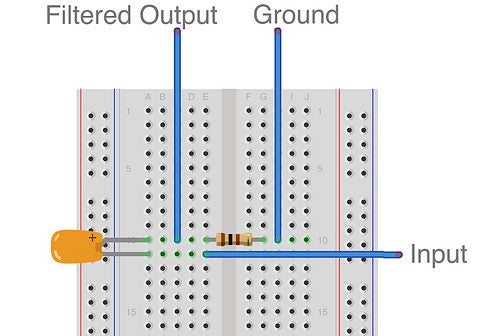
您的输入信号首先被馈入电容器,该电容器的另一端连接到电阻器,该电阻器的另一端连接到地。您的输出信号应在电容器和电阻器之间读取。
进行测试以确保其正常工作。
如果您无法使用函数发生器或示波器,则可以必须相信我们为您正确测试了电路。我们构建了如下所示的电路:
红色的鳄鱼夹夹住了来自函数发生器的输入信号,黑色的鳄鱼夹夹住了地,绿线承载我们的输出信号,然后将其发送到示波器进行测试。当我们从低频信号变为高频信号时,我们在示波器上读取的结果看起来像这样:
黄色曲线是我们的输入信号,蓝色曲线是我们的输出信号(请注意,尽管黄色曲线看起来保持不变,这是因为我们正在改变示波器显示屏上的频率缩放比例)。在低频下,您可以看到整个信号都被滤除,几乎没有输出信号。随着频率的增加,输出信号会变大,直到达到与输入信号几乎相同的点为止。这称为截止频率,稍后我们将向您展示如何找到它。您还应该注意,输出信号可以与原始输入信号相移,这意味着尽管信号具有相同的频率,但不一定一定是“同步”。
另外,请注意,虽然我们有意一次输入了一个均匀频率的信号,但该电路将对复合信号起作用。
截止频率
计算截止频率。
截止频率通常被认为是信号衰减(或滤波)的频率。这意味着频率低于截止频率的任何信号都被视为已滤波,而频率高于截止频率的任何信号均被视为“左撇子”或未滤波。那么截止频率是多少?

其中, R 是电阻的电阻,单位为Ω, C 是电容器的电容,单位是 F 。
信号的截止频率是什么意思?
如果您看一下在很宽的频率范围内输出信号的幅度与输入信号的幅度之比,您将得到如下效果

请注意,两个轴都是对数缩放的。这实际上意味着,如果您从一条浅灰色线向上移动到下一条灰色线,则您的值实际上会增加10倍。这意味着,如果您在没有对数刻度轴的情况下查看此图,则实际上会看到截止频率几乎垂直下降。但是,频率高于截止频率的任何信号或信号成分都未经滤波,可以很好地近似。
输出信号与输入信号相移。
前面我们说过,输入和输出信号不是“同步”的,而是实际发生了移位。这对于某些应用程序可能很好,但是在其他一些应用程序中这可能很重要。随着输入信号频率的变化,相移也随增益的变化而变化,并且这种变化的曲线看起来像这样。

频率时,输出信号相移π/2,而在高频时,相移几乎为零。截止频率对于相移很重要,因为它是输出信号相移恰好是π/2或π/4的一半的频率。
您如何获得这些结果? !?!
如果您真的想知道,请查看理论部分,以获取有关电路工作原理以及我们如何计算增益和相移的更多信息。
TL; DR
高通滤波器可以按以下方式制造:
输入-电容器-(输出)-电阻-接地
高通滤波器滤除频率低于截止频率(1/2πRC)的信号。
由于截止频率由R和C严格确定,因此请选择适当的电阻器和电容器来截止您想要的频率
输出信号与输入信号相移。
步骤2:低通滤波器

此部分的内容与“高通滤波器,因此,如果您已经读过它,那么在那里发现的许多信息也将适用于低通滤波器,除了几乎所有的东西都翻转了。
您需要的东西
要放入电路中的东西:
一个电容为C(在 F 中的电容器)。
一个电阻为R(在Ω中)。
输入信号(我们来自函数发生器)。
示波器(用于测试)。
您将从电路中获得的收益:
经过滤波的输出信号。
如何构建电路

零件在哪里?您的输入信号首先被馈入电阻器,该电阻器的另一端连接到电容器,而电容器的另一端则连接到地。您的输出信号应该在电阻和电容之间读取。
进行测试以确保其正常工作。
如果您无法使用函数发生器或示波器,则可以必须相信我们为您正确测试了电路。我们构建了如下所示的电路:
红色的鳄鱼夹夹住了输入信号(来自函数发生器),黑色的鳄鱼夹夹住了地,绿线承载我们的输出信号,然后将其发送到示波器进行测试。当我们从低频信号变为高频信号时,在示波器上读取的结果如下所示:
黄色曲线是我们的输入信号,蓝色曲线是我们的输出信号(请注意,尽管黄色曲线看起来保持不变,这是因为我们正在改变示波器显示屏上的频率缩放比例)。在低频下,您会看到几乎没有信号被滤波,并且我们的输出几乎与我们的输入相同。当频率达到截止频率时,输出信号开始明显小于输入信号。从这里开始,随着频率的增加,输出信号变得越来越小,直到几乎没有信号剩下为止。您还应该注意,输出信号可以与原始输入信号相移,这意味着尽管信号具有相同的频率,但不一定一定是“同步”。
另外,请注意,虽然我们有意一次输入了一个均匀频率的信号,但该电路将对复合信号起作用。
截止频率
计算截止频率。
截止频率通常被认为是信号衰减(或滤波)的频率。这意味着,频率高于截止频率的任何信号都被视为已滤波,而频率低于截止频率的任何信号均被视为“独立”或未滤波。那么截止频率是多少?

其中, R 是电阻的电阻,单位为Ω, C 是电容器的电容,单位是 F 。
信号的截止频率是什么意思?
如果您看一下在很宽的频率范围内,输出信号的幅度与输入信号的幅度之比,您会得到如下效果

请注意,两个轴都是对数缩放的。这实际上意味着,如果您从一条浅灰色线向上移动到下一条灰色线,则您的值实际上会增加10倍。这意味着,如果您在没有对数刻度轴的情况下查看此图,则实际上会看到截止频率几乎垂直下降。但是,频率低于截止频率的任何信号或信号成分都未经滤波,可以很好地近似。
输出信号与输入信号相移。
前面我们说过,输入和输出信号不是“同步”的,而是实际发生了移位。这对于某些应用程序可能很好,但是在其他一些应用程序中这可能很重要。随着输入信号频率的变化,相移也随增益的变化而变化,并且这种变化的图看起来像这样。

在高频率下,输出信号相移为零,而在高频下,相移几乎为π/2。截止频率对于相移很重要,因为它是输出信号相移恰好是π/2或π/4的一半的频率。
您如何获得这些结果? !?!
如果您真的想知道,请查看理论部分,以获取有关电路工作原理以及我们如何计算增益和相移的更多信息。
TL; DR
低通滤波器可按以下方法制造:
输入-电阻-(输出)-电容器-接地
低通滤波器滤除频率超过截止频率(1/2πRC)的信号。
由于截止频率由R和C严格确定,因此请选择适当的电阻器和电容器截止频率。
输出信号从输入端移相。
步骤3:带阻和带通滤波器

我们将仅简要讨论陷波滤波器和带通滤波器在这里。这些只是此类过滤器的最基本版本,因此只能满足最基本的需求。
陷波/陷波/挡带过滤器
这是什么?
带阻滤波器是一种电路,可以理想地滤除频率在一定范围内的信号。该范围可能很大,具体取决于电路的固有特性。电路滤波的频率范围越小,据说它的 Q 系数就越高。具有高 Q 因子的带阻滤波器也称为陷波滤波器。
构建一个简单的陷波滤波器。
使用电阻器,电容器和电感器,您可以构建一个简单的陷波滤波器,如下所示:
它可以滤除哪些频率?
中心频率,也称为可以在该电路周围进行滤波的谐振频率可以找到

,其中L是 H ,C是 F 中电容器的电容。
带通滤波器
是什么
带通滤波器是理想地滤除除特定范围内的所有频率之外的所有信号的电路。该范围可能很大,具体取决于电路的固有特性。电路允许通过的频率范围越小,据说它具有的 Q 因子就越高。
构建一个简单的带通滤波器。
使用电阻,电容器和电感器,您可以按如下所示构建一个简单的带通滤波器:
它允许通过哪些频率?
可以使电路通过的中心频率或谐振频率类似于

,其中L是电感的 H 中的电感,C是 F 中电容器的电容。
步骤4:滤波电路背后的原理
来自xkcd.com的图像。
此处的此步骤仅是为了沉迷您的科学好奇心和
分压器
什么是分压器?
顾名思义,分压器是吸收电流的电路输入电压并输出等于输入电压一部分的输出电压。电路本身就是一个电压源,它与两个电阻串联,两个电阻之间的输出如下所示。

了解分压器工作原理的关键是知道电流 I 在整个如果在输出端没有汲取电流,则两个电阻器都将输出。使用欧姆定律( V = IR ,电压=电流x电阻),我们看到两个电阻中每个电阻的压降与电阻成正比。例如,如果电阻具有相同的电阻,则输入电压将在两个电阻之间平均分配。换句话说(实际上得到输出电压的公式),让我们使用欧姆定律根据输入电压和总电阻来计算电路的电流。

现在再次使用欧姆定律根据输出电压计算电路的电流。

第二个电阻上的压降为等于输出电压。请注意,正如我们之前所说,这两个电流相等,因此我们可以将两个方程式设置为相等,并求解输出电压。

这表明输出电压取决于第二个电阻器的电阻与两个电阻器的总电阻之比。
一个简单的例子

电容器的阻抗
您可能已经注意到,我们的高通和低通滤波器只是分压器,其中一个电阻替换为电容器。因此,我们可以在理论上进行与上述相同的分析,以了解滤波器的工作原理,但是首先我们需要了解阻抗。
您可以将阻抗视为广义电阻。例如,众所周知,电阻器的阻抗称为电阻。电阻器的阻抗仅为R,即电阻值,但是电容器的阻抗是多少?阱电容器的阻抗用复数值1/(jωC)表示,其中C是电容器的电容,ω是通过电容器的信号频率,以弧度表示(ω=2π f ,其中 f 是频率(以赫兹为单位),而j只是虚数 i =√-1,(我们使用j代替i,所以我们不会混淆它
注意电容器的阻抗与频率有关。对于接近零的频率,电容器的阻抗变为无穷大,但是,对于非常高的频率,其阻抗变为零。换句话说,电容器的阻抗在低频下看起来像是一个大电阻,在高频下就像一条没有电阻的简单导线。
了解高通和低通电路
您还记得确定分压器输出的方程式

如果将其推广用于阻抗,我们将得到类似

其中 Z 只是我们电路元件的阻抗,而波浪线或波浪线仅表示我们正在处理复杂的信号数字。对于低通滤波器,我们在顶部有一个电阻,在底部有一个电容,所以

这看起来有点讨厌,但是如果我们简化一下,我们得到

还不错吧?
最后一个公式是理解为什么低通滤波器仅对高频进行滤波的关键。注意,对于低频,jωRC近似为零,因此输出电压近似等于输入电压。现在对于高频,jωRC近似为无限,因此我们得到输出电压几乎为零。看看这是如何工作的?当我们的复数电压(由不同频率的各种波组成)用作滤波器的输入电压时,电压的高频部分产生的输出电压等于零,而低频部分产生的输出电压等于输入电压(即我们只获得信号的低频部分)。
应用于低通滤波器的相同论点可以用于高通滤波器,只需切换电阻器和电容器的位置。我们仍然使用相同的公式

但是,这次

如果我们简化,我们应该再次得到

对于高频,我们基本上得到jωRC≈jωRC+ 1,所以我们应该得到一个等于输入的输出电压电压。对于低频,我们得到jωRC≈0,因此输出电压几乎为零。如您所见,正如我们所承诺的那样,我们跳过了高频,只滤出了低频。
截止频率
如前所述,截止频率对于高通或低通滤波器电路,要知道一个非常重要的值。我们实际上如何找到它呢?截止频率定义为输出电压精确等于输入电压的1/√2的频率。这是滤波器开始衰减输入信号的点。如果使用上面的方程式求解该频率,则会发现

,其中ω=2π f 。如您所见,截止频率严格取决于我们为电阻和电容选择的值,因此我们可以准确选择希望电路开始过滤信号的位置。
责任编辑:wv
-
滤波器电路
+关注
关注
2文章
75浏览量
24477
发布评论请先 登录
相关推荐
无源滤波器的影响因素
LC滤波器和RC滤波器有哪些差异
高通滤波器电路属于直流电路吗
emi滤波器是什么滤波器
高通滤波器和低通滤波器判别方法
有源滤波器和无源滤波器的原理及区别是什么
低通滤波器电路图分享
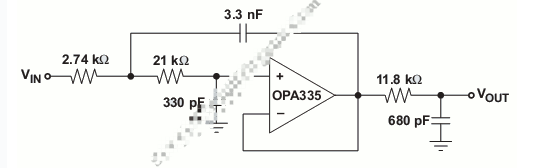




 如何制作多种不同的滤波器电路
如何制作多种不同的滤波器电路











评论