Σ-Δ模数转换器(ADC)威廉希尔官方网站 一览

摘要

Σ-Δ模数转换器是从脉宽调制器类积分型ADC演变而来的，其interwetten与威廉的赔率体系 部分相对容易实现、数字部分则比较灵活。随着威廉希尔官方网站 的发展，Σ-ΔADC基本原理已结合不同量化器形成了有意义的变种。本应用札记回顾了与Σ-ΔADC相关的重要概念与拓展：过采样、（量化）噪声整形、（量化）噪声调制、数值化、滤波抽取，以及残量累积和局部精细量化（Zoom）等变种。

目录

1 Σ-Δ ADC概述... 2

2 过采样量化噪声整形和量化噪声调制... 4

2.1 量化噪声与ADC的分辨率... 4

2.2 过采样量化噪声整形与ADC的分辨率... 5

2.3 量化噪声调制... 6

2.4 改善量化噪声抑制收敛速度以及阶数的概念... 8

3 抽取和滤波... 9

4 改进和变种... 10

4.1 局部放大（Zoom）Σ-Δ型ADC. 10

4.2 残量继承电容DAC SAR预量化Σ-Δ型ADC[4][5][6] 11

参考资料... 11

以1作为量化门限时，0.7被量化为0；无论多少次采样0.7保持被量化为0。只有1这一个量化台阶的Σ-Δ型ADC经过反复量化可以得到0.7；Σ-Δ量化的基本原理是从多次量化中抽取其统计分布中心，结合其它量化方案可以加快误差收敛速度和提高量化分辨率。关于Σ-Δ型ADC的文献最早出现于1962年[1]，早期的原理讨论淹没在了深化研究之下。本札记试图钩沉这些早期原理讨论，为理解Σ-Δ型ADC做入门铺垫。

1 Σ-Δ ADC概述

图 1是介绍Σ-Δ型ADC工作原理时常见的顶层框图，图中将Σ-Δ型ADC表达为Σ-Δ调制器和数值抽取滤波器两个环节。该图表达了Σ-Δ型ADC的两个关键特征，其一是有一个调制过程在一个时间段内使调制量与模拟输入相互作用，其二是以k×fs的过采样速率获取速率为fs量化输出。采样孔径[1]指量化输出反映的模拟输入片段的整体效果。就Σ-Δ型ADC而言，对调制状态流采样需要持续时间、滤波器需要状态建立时间，表现为采样孔径大、输出延迟大。采样孔径的大小和输出延迟表现为量化过程的幅频特性和瞬态响应特性。

图 1 Σ-Δ型ADC顶层框图

图 1是概念性框图，图 2则是具体以脉宽调制器为Σ-Δ调制器的Σ-Δ型ADC的功能框图，方便更具体地说明其各个局部的功能。该电路中调制器的状态流为脉宽调制器的占空比信号，调制量流是受占空比信号控制的、相对于中间值电压VCOM的±VREF偏移电压。VX的范围限制在VCOM±VREF范围内。

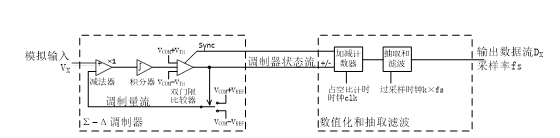
图 2 具体基于脉宽调制器的Σ-Δ型ADC的功能框图

当调制量流为VCOM-VREF时，减法器输出为正，积分器输出逐渐增大。直到积分器的输出超过上阈值VCOM+VTH，双门限比较器输出翻转、将调制量流输出切换为VCOM+VREF。由于VX幅度在VCOM±VREF范围内，上述切换后积分器输出逐渐变低。积分器输出变低最后会超出下阈值VCOM-VTH，双门限比较器输出翻转、将调制量流输出切换为VCOM-VREF方波幅度流。当VX=VCOM时，调制器状态流输出占空比D=1:1；当VX与VCOM不同时，占空比D反映VX偏离VCOM的程度，即D=0.5 + (VX-VCOM)/(2×VREF)。或者，在中心值为0时，VX=2×(D-0.5)×VREF，即VX决定了占空比偏离1:1的程度。调制器的状态流是对积分器输出的量化结果，该结果影响调制量流，但不是对VX的量化。VX通过调制器反映为调制器状态流的占空比，这个占空比由图中加减计数器读取，计数器的值为VX的量化值。在一个周期内占空比计数器的量化误差反映为调制器状态翻转时间与计时时钟clk对齐的偏差，即可能存在一个时钟周期的偏差。重复多个周期，总计数时间不断增大，这一个周期的量化误差占比不断减小。这种通过多个周期不断累积获得精确占空比的过程即抽取[2]过程。由于VX是变化的，过长的累积过程会掩盖掉VX的变化，上述累积需要利用具备一定时间常数的数值滤波器实现，即抽取和滤波是同时由滤波单元实现的。

上述原理介绍中没有提及图 2中Sync信号的功能，该功能与Σ-Δ型ADC设计方案的演化相关。图 2电路是典型的早期雏形积分型ADC；如果Δ代表差值、Σ代表积分，则此雏形电路应为Δ-Σ型ADC（部分文献[1]仍采用Δ-Σ的命名）。Sync信号的引入取代了早期Σ-Δ型ADC方案中的加扰电路（dither），利用它在积分环节引入了一个残差，亦可用Δ表达。引入Sync信号后，该类型的ADC则名副其实地称为Σ-Δ型ADC了。上述残差与加扰电路的功能一致，用来保证量化误差能在一定范围的量化台阶内均匀分布。这个保证量化误差均匀分布的功能即（量化）误差调制，将在下文2.3中进行详细讨论。

Σ-Δ型ADC本质上或者底层原理是利用多次采样取平均将量化误差对消。无论是图 1还是图 2，用来分析量化噪声的调制如何改善信噪比都太过具象，通常利用图 3所示的一般模型做理论分析。该模型中，带有量化噪声的量化结果被送回到输入与输入模拟量相减合并到下次量化中；如果每次量化作为一个迭代周期，则每次迭代量化误差的极性是翻转的。如果量化误差是完全随机的，即出现正随机误差和负随机误差的几率一致，则经过充分迭代后，量化误差反复加减后会趋于零。图 3中输入到ADC的是VH，但ADC的输出并不是VH，而是根据一段时间内VH的变化得到的VX量化值DX；对VX的量化过程是从对VH量化提取得到的。直观的解释是重复对VX做多次采样取其平均值，有正有负的量化误差被平均过程减小了。

图 3 分析Σ-Δ型ADC中量化噪声改善影响的一般结构框图

Σ-Δ型ADC的三个关键特征分别是，过采样过程将量化噪声推到高频、在大量数据中抽取出量化值及滤波、以及保证量化噪声的平稳和均匀分布。

2 过采样量化噪声整形和量化噪声调制

借助于奈奎斯特采样的分析方法从信息提取角度可以导出过采样过程如何提高量化精度的一般性解释。首先，仍需要假设量化噪声是平稳和均布的，以及过采样数据处理过程不引起信息损失，即仅考虑过采样时的量化误差。以下将解释如何从信息提取的角度评估量化噪声与ADC位长的关系以及将量化噪声调制在量化台阶内的实施例。

2.1 量化噪声与ADC的分辨率

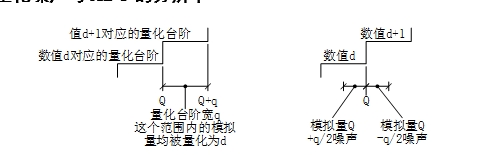
图 4 理解量化台阶和量化噪声的示意图

参考图 4左图，不局限于Σ-Δ型ADC，量化台阶指对应相邻两个量化值的模拟量范围，在这个范围内模拟输入都被量化为同一个数值，即图中的d。记d临界变化的模拟量是Q，相邻数值d+1临界变化对应模拟量为Q+q，则数值增量1对应的模拟量增量q即量化台阶。对于线性量化过程，这个台阶即最小量化权值位LSB（less-significant bit）对应的模拟量范围。这种将模拟量量化为数值时，因数值表达的不连续性导致的误差即量化误差。将量化误差看作噪声影响时其效果相当于在模拟量上叠加了幅度在-q~0范围内的噪声。考虑这个噪声是均匀分布的，则平均值为-q/2，即图 4左图所表达的量化误差从统计结果看同时引起统计零点出现-q/2的漂移。这个漂移可在数字域或模拟域移除，从而可以将量化噪声反映为如图 4右图所示的-q/2~+q/2的噪声，即量化结果d对应较Q低的实际输入量叠加了同相噪声或较Q高的实际输入叠加了反相噪声。此时在-q/2~q/2范围均布的噪声的均值为0（在-q/2~0范围内均值为-q/4，在0~q/2范围内均值为q/4），方差密度或噪声密度为σ= ，式中A为幅度，σ为能量或方差。有限次量化时，n次量化噪声平均幅度在正和负两个部分分别为正和负(q/4)/(n1/2)[3]。相对于单次量化时在两侧的均值q/4，随着量化次数的增加，均值以1/n1/2速度缩小。由于噪声能量总是正值，量化次数不改变平均到每次的噪声能量，而只是改变其短期统计偏差与长期统计偏差的偏离程度。

长期且平稳时，信号能量密度与噪声能量密度为1:1的相对关系用来表述一个信息表达系统的极限能力；量化系统极限有效动态范围以信号/量化噪声比SINAD表达为10×lg(Ps/Pn)（dB），其中Ps为信号能量密度，Pn为噪声能量密度。对于N位ADC，其不失真地采样一个正弦信号的幅度为2N×q/2，其能量为22×N×q2/8，前述极限有效动态范围为10×lg[(22×N×q2/8)/(q2/12)]，即SINAD=1.76+6.02×N。由此可看出，位长N与信噪比的正比关系。从另一个角度看SINAD的表达，如果一个量化系统在原始采集到的数据基础上的后续处理过程中数字表达不受位长限制，降低Pn可获得更高的SINAD。即，如果平均过程可以降低量化噪声平均幅度，则可借助平均过程获得更高的SINAD。

2.2 过采样量化噪声整形与ADC的分辨率

2.1中已说明重复n次采样和量化时平稳和均布的量化噪声以1/n1/2的比例减小，以及如果处理过程不受位长影响，量化噪声的减小相当于有效位长增加。将其中SINAD的公式改写为N=(SINAD-1.76)/6.02=[10lg(Ps/Pn)-1.76]/6.02，带入n增加时量化噪声幅度减小1/n1/2的比例关系后，得到n每增加一倍，等效位数增加0.5位的关系[4]。需要注意，此处的量化噪声能量并不是多次量化的平均量化噪声能量，而是从平均量化噪声幅度折算得到的等效值。多次采样取平均只是多种数据处理方式之一，从量化噪声能量变化的角度可导出过采样改善ADC分辨率的一般性关系。

当以fs为采样速率对模拟信号采样时，如图 5所示，带宽为fa的模拟信号及其镜像部分经采样后被搬移到以fs频率的两侧。奈奎斯特采样定律指出最低限度地识别信号频谱的极限情况出现在fs=2×fa时；当fs＜2×fa时，fa频谱中高于fs/2的部分出现交错，致使该部分的功率高于实际信号功率，从而导致误判。在临界情况下，即fs=2×fa时，采样过程将量化噪声调制到了带宽为fs的采样频谱中，这时量化噪声的影响最大。

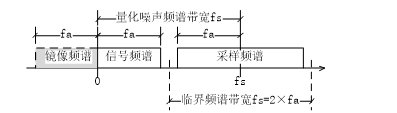
图 5 采样对模拟信号频谱的搬移

量化噪声可能出现的最高频率即采样频率fs，作为白噪声时在0频率到fs间均布。当信号带宽小于fs时，则只有fa/fs比例的量化噪声被调制入采样频谱。记fa/fs=1/n，则量化噪声可以调制到采样频谱中的部分为1/n。将这个关系带入公式N=[10lg(Ps/Pn)-1.76]/6.02中，即得到只有部分量化噪声进入采样频谱时ADC分辨率改善的一般关系[5]。

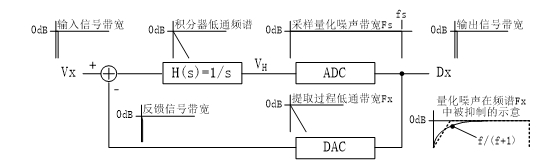
图 6 增加了频谱示意的抽象结构框图

图 6在图 3所示的抽象结构基础上增加了信号带宽和传递函数带宽的示意，明确了以积分器作为简洁的模拟低通滤波器限制量化噪声频谱的一般性特征，没有明确ADC的形式和DAC的形式及其反馈延时关系。分析上图，传递方程为DX = (VX-DX)×H(s) + qN，在低频范围不考虑相移影响，上述方程可简化为DX = (VX-DX)/f + qN，可推导出DX = VX/(f + 1) + qN×f/(f + 1)，该导出式显现对于极点为零的积分器型滤波器，当f接近零时，量化噪声的影响也接近零。由此可见，对量化噪声的抑制是由滤波器H(s)、对VH量化和从中提取对窄带的VX量化结果的（滤波）过程中实现的。

以上即量化噪声整形的一般性概念，利用过采样使量化噪声分布在很大带宽内，然后只保留有限带宽内的量化噪声，从而取得比过量化量化器高的有效位长。过采样和量化噪声整形的概念并不局限于低通方式，也包括对高频窄带信号（相对于带通带宽的）过采样和利用带通滤波实现噪声整形的情形。

2.3 量化噪声调制

量化噪声调制是使量化噪声呈现白噪声或者接近白噪声的过程。量化器本身不能保证多次量化过程中量化噪声是均匀分布的。例如当模拟量在一个量化台阶内保持稳定时，无论是多少次采样所采集的数据是个确定值，则无论如何抽取和滤波，都不会改变量化噪声的幅度，从而无法提高有效位长。图 3中利用DAC将量化结果反馈到前端与输入信号相减的过程在每次迭代时翻转量化误差极性可以加快量化误差的收敛速度，但仍不能使处于一个量化台阶中的稳定输入引起不同输出，因此也无法使量化误差均布。

Σ-Δ型ADC的早期设计中曾使用主动加入扰动的方式使多次量化的结果在若干位间以输入模拟量为中心对称分布。利用加入扰动的产品实例可见MAX110/111[2]（ADI公司产品），其利用一个扰动产生单元（dither generator）产生一个对称分布的准白噪声使对稳定输入信号的量化结果出现在不同编码上；量化结果的统计分布中心即加扰后的模拟信号的中心，而该统计中心位置精度由统计样本规模决定、不受量化器精度限制。后期设计中很少使用加扰，但加扰方案中由多个量化台阶上的样本数决定统计分布中心的精髓得以延续；利用取多个台阶的平均值改善台阶幅度偏差。

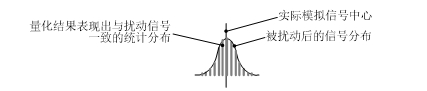
图 7 利用加扰使多次量化结果以输入量为中心分布的示意

图 2中的Sync信号利用比较器翻转时间与一个稳定的计数时钟的偏差来产生一个残量（即文献[3]第16、17页提到的线性时间变量）。这个残量的幅度在一个Sync时钟间隔内均匀分布，完全符合Σ-Δ型ADC的需要。带有同步信号的比较器，即锁存比较器，在Sync信号前沿瞬时将输入接入一个双稳态触发器；无论输入幅度差是多少，这个双稳态触发器一定会产生唯一的逻辑状态，是一种高增益比较器。锁存比较器只在Sync信号前沿瞬时检查获取输入幅度信息。如果过阈值的临界状态出现在两个Sync信号前沿之间，临界时间与比较器输出之间出现延时；在这段延时期间积分器保持原来的状态，输出在过阈值后继续变化。

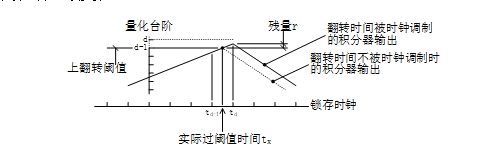
图 8 翻转时间被时钟调制产生残量的示意

图 8说明了上述延时如何产生在一个量化台阶内随机均布的残量，以及这个残量带入下一个积分过程的情形。如图所示，以过上翻转阈值为例，实际过阈值时间发生在tx时刻，但直到td时刻锁存比较器才检查积分器输出。从过阈值到锁存比较器输出翻转、改变积分器的变化方向，积分器输出仍沿着之前的方向变化并产生了一个与td-tx时间有关的残量r。这个残量r使得积分器在下一个方向上的变化的起点偏离了量化台阶的端点，是对其计时过程的扰动。考虑tx与时钟无关，同时在td-1~td的时间范围内积分器输出的变化不大，则残量r在一个量化台阶内均布。对于经常采用的一位量化器而言，残量r是积分器输出超出上下翻转阈值的部分。对于图 2所示脉宽计数结构的电路来讲，残量r则是均匀分布在d-1和d之间的随机扰动。除扰动加入方式不同外，图 2电路与产品实例MAX110/111一样，单次量化器是多位精度的脉宽计时器；这个单次量化器的分辨率或位数对应积分器一个完整充放周期的计时。

Σ-Δ型ADC的关键特征是在单次采样量化后的数据处理，这是一种广义的积分过程，即需要某种方式让多次量化的结果关联起来；这种情况下单次量化被称为预量化，后续的处理仍被称作抽取和滤波过程。其中单次量化器则不局限于积分变换器，例如可以采用基于电荷平衡的逐次逼近型的SAR ADC。电荷平衡SAR ADC可借助其权电容将上次变换所剩余的残量带入下次变换采样中，实现量化噪声调制[4]。

量化噪声调制过程同时作用到其它类型由量化器引入的低频噪声。部分残量由量化器的低频噪声引起，这部分没有计算到积分时间内的残量在下一个方向的积分过程中以反向的形式导致积分的起点向延长积分时间的方向移动。在接续的两个积分过程中，量化器引入的噪声分别表现为正和负的影响，相当于利用以积分时间为周期的±1极性对称方波进行了调制。考虑其作用的一致性，进一步的讨论中不必区分量化噪声和其它类型由量化器引入的噪声。

2.4 改善量化噪声抑制收敛速度以及阶数的概念

利用快速预量化可直观和直接地改善收敛速度，大多改进出现在积分调制器和抽取滤波部分（自从1962年这个分类被提出后，大量研究和产品实践都是围绕调制器和抽取滤波展开的[1]）。本小节试图提供有助于理解这些创造的一般概念，而不是尝试概述。

将图 3表达为以固定节拍迭代的离散过程，见图 9。类似地，图 9只是表达数据提取部分是对之前输入的量化、仅将量化误差反向后送回积分的概念，而忽略了其具体实现的复杂性。这个过程的z域表达为D(z) =z-1×X(z) + (1 – z-1)×Q(z)；其中从X(z)到D(z)以1:1增益传递，Q(z)为量化误差序列，z-1代表一个延迟节拍，(1 – z-1)为积分器（与1/s或f/(f + 1)对应的）在零频率上的陷波函数。其收敛速度慢表现在由f/(f+1)反映的关系上，只有当fs>> fa时才能对量化误差的有效抑制。

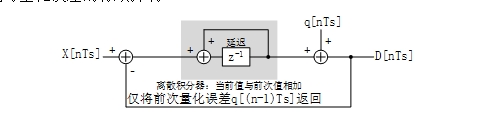
图 9 以离散过程表达的Σ-Δ型ADC的结构

直观的改善办法是尝试堆叠调制器积分节，使传递函数与积分器相关的部分连续延迟-相乘的关系表达为D(z) =z-1×X(z) + (1 – z-1)L×Q(z)；其中L为级联次数。以三阶级联为例，相应的传递模型如图 10所示；其中系数a1~a3表示在累积延时-积分时的传递增益需要控制。这个级联次数L即所谓Σ-Δ调制器的阶数。(1 – z-1)L被称为量化噪声整形函数，图 11是其在0~0.5fs频率范围的模值。

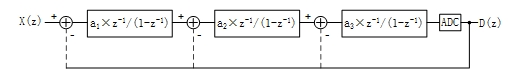
图 10 对量化误差做三阶级联积分的模型

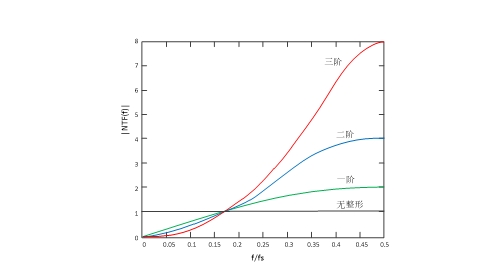
图 11 整形函数(1-z-1)L在0~0.5fs频率范围的模值

(1 – z-1)L的模值为[2×sin(π×f/fs)]L，是2×fs的周期函数。其在零频率附近的斜率变化与L阶幂函数一致，使得L增大时在低频部分残余的量化噪声快速下降。每增加一次级联相应增加一个延时单位，同时在较高频率上的传递增益快速增加（在f = fs/2处增益为2L）。使用高阶结构时需要插入滤波器控制传递增益或者采用高位长的预量化器来减小量化噪声的相对幅度以防止出现自激。

3 抽取和滤波

过采样产生的大量数据需要在第一时间压缩和提取有效部分，以便减小后续需要处理的数据量。这部分处理即抽取（decimation）或退过采样（down-sample）。具体实施均采用对一段时间内采集的数据连续加和获取平均值的方式来实现。连续加和即离散积分的过程，不需要中间数据寄存器即可完成。如果一个时间片完成后再启动下一个时间片，则只有完成一次整时间片的加和才能看到数据的变化，处理延时长并且对变化不能快速响应。普遍利用滑动平均（moving average or sliding average）在平均样本数和快速响应间折中。M阶的滑动平均需要存储M个中间数据，每输入一个新数据同时放弃一个最老的数据，然后以新的M个数求取平均值。滑动平均仅需要加减操作和桶形结构先入先出寄存器组即可实现。当过采样比较大时可能需要采样分片加和级联多次滑动平均的方式减少电路规模，这时的每个处理节称为分段预采样。分段预采样的离散转移关系为 ，传输函数z域表达为(1-z-M)/[M×(1-z-1)]。当M为1对应分片加和的情况，幅频响应为SINC函数；M阶滑动平均相当于按M次倍频嵌套相乘多次SINC函数，可以改善最低频的SINC在低频部分的平坦度和陷波频率点附近的衰减速度。这种多次嵌套SINC的幅频图上可见在最大滑动区间对应的频率处出现一连串陷波频率点，因其曲线形状也被称为梳状滤波器[1]。

经过梳状滤波器后数据流速率得以降低，而后接入滤波器可以减小滤波电路的规模。对于窄带应用的输入频率相对于实际需要的带宽仍然可能过高，还是需要利用级联方式将滤波器分节实现，以便减小电路规模。

4 改进和变种

使量化噪声均布，然后利用过采样和抽取过程减小量化噪声的基本原理配合多种类型ADC实现折中的性能改善。以下介绍常见的局部放大（Zoom）Σ-Δ型ADC和基于电荷平衡的残量继承电容DAC SAR预量化Σ-Δ型ADC。

4.1 局部放大（Zoom）Σ-Δ型ADC

利用其它高速或中速ADC，例如采用SAR ADC，快速预量化输入模拟量后，将预量化结果快速带入抽取和滤波逻辑，以预量化值为起点可以加快向更精确量化结果的收敛速度。如果只是用来预置收敛过程的起点，Σ-Δ调制器的输出摆幅不变，调制器部分的时间预算不会降低。

将预量化结果利用DAC还原为模拟量，将输入减掉还原模拟量得到一个差值，将此差值送入一个Σ-Δ型ADC则可以使Σ-Δ调制器只作用在差值所对应的局部。此实现方式的ADC即局部放大（Zoom）Σ-Δ型ADC，原理图见图 12。

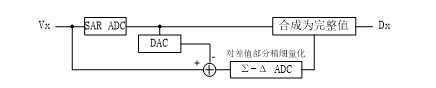
图 12 局部放大（Zoom）Σ-Δ型ADC的原理

局部放大型ADC适合要求对局部做高精度解析的应用，例如在大尺度测量时获取以节距为参考的定位，以及测量围绕某个中心值的弛豫过程。在这些应用中节距或者中心值的精度要求与围绕节距和中心值的变化的精细要求不同，需要局部放大和量化。从动态范围角度看，局部放大的获益局限于其Σ-Δ ADC所处理的局部；全局的量化特性受预量化ADC和还原DAC的制约。局部放大型ADC可以快速输出预量化值，用于节距定位，也能以慢速Σ-Δ型ADC的方式获得精细解析结果。

4.2 残量继承电容DAC SAR预量化Σ-Δ型ADC[4][5][6]

利用电荷平衡型的电容DAC做SAR型ADC时，完成逐次逼近的节拍后、权电容阵列上会残留一个或正或负的电压。这个电压对应一个电荷残量，如果将这个残量带入下次量化，则相当于实现了量化噪声调制。相对于图 2所示或产品例MAX110/111的脉宽计数预量化和量化噪声调制，残量继承可以快速实现残量调制和预量化，其整体电路结构也比前述局部放大型的结构紧凑。在这种结构方案中，预量化和残量调制是同一个过程的两个结果，是最快的噪声调制方式。对一次预量化而言，残量在一个量化台阶内是均布的；从多次量化间逐次继承来看，该残量的累积影响了下次变换结果，即在SAR ADC结果中包含了一个积分ADC作用。当除量化噪声外的其它噪声影响不大时，积分型量化变换的分辨率与积分时间成正比。以过采样倍数n来表达，残量继承预量化对位长改善能力在n1/2~n之间，高于单纯以随机噪声所做的测算。

参考图 12所示的原理，SAR量化结束后的残量即该次采样与该次量化还原值之间的差值。与局部放大型(Zoom)相比，每次量化的还原值可能是不同的（因量化噪声之外的扰动）。这导致预量化结果的变动，使预量化的微分非线性影响进入差值。这个影响同样会经过抽取滤波过程被均化和减小。进一步地，如果有意随机地提前结束逐次逼近，可将残值扩大到多个位，进而利用抽取滤波在多个位之间均化其微分非线性的影响。

参考资料

[1] Philips E. Allen, Douglas R. Holberg. CMOS Analog Circuit Design[M]. 2nd ed. Oxford University Press, Inc., U.S.A., 2002.

[2] Analog Devices, Inc. MAX110/MAX111 Data Sheet[EB/OL]. (1998-11). https://www.analog.com/media/cn/technical-documentation/data-sheets/1018.pdf.

[3] Shanthi Pavan, Richard Shreier, Gabor C. Temes, Understanding Delta-sigma Data Converters[M]. 2nd ed. Wiley-IEEE Press，2017.

[4] 雷鑑铭，刘佳明，马常乐，谭磊，白玮. 一种基于残量累加电荷的逐次逼近型数模转换器：202210664014.8[P]. 2022-06-13.

[5] 谭磊. 一种模数转换器及其操作方法：202111617749.7[P]. 2021-12-27.

[6] 白玮，谭磊，于翔，谢程益. 模数转换器：202111597874.6[P]. 2021-12-24.

修订记录

重要声明

SGMICRO保留更改电路设计、产品规格和产品描述的权利，恕不另行通知。

本文档内容仅供参考。本文档中的所有陈述、信息和建议不构成任何承诺。对于本文档中可能出现的错误，以及因本文档提供的信息和使用本文档而造成的任何附带或间接损失，本公司不作任何明示或暗示的陈述和保证。

此文档未授予任何知识产权许可。除了SGMICRO在其产品的销售条款和条件中声明的责任外，本公司概不承担任何其他责任。