高速电路设计领域,关于布线有一种几乎是公理的认识,即“等长”走线,认为走线只要等长就一定满足时序需求,就不会存在时序问题。本文对常用高速器件的互连时序建立模型,并给出一般性的时序分析公式。为体现具体问题具体分析的原则,避免将公式当成万能公式,文中给出了MII 、RMII、RGMII和SPI的实例分析。实例分析中,结合使用公式分析和理论分析两种方法,以实例证明公式的局限性和两种方法的利弊。
本文通过实例指明时序分析的关键在于:对具体时序理解透彻的基础上,具体问题具体分析,不能一味的套用公式,更不是通过走线的等长来解决时序问题。
1. 典型高速器件互连时序模型
图1给出通用高速器件互连接口简化模型。图中,左侧虚线框表示通信器件双方的主控端。常见的实际情形有:SDRAM控制器、SPI主控制器等。经过适当的演化,基于本模型很容易得到I2C主控端、MII接口的TX组模型、RMII共享时钟模型以及DDR控制信号与地址信号的互连模型等。右侧虚线框表示通信中的被动端。本模型中,数据是双向的,但是时钟是单一方向。简单地说,就是时钟单一方向发送,数据双向传递。这个特点是本模型的适应场景。
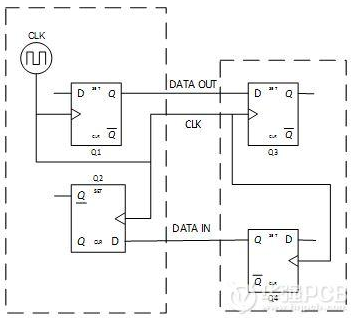
图1 高速电路设计_简化的器件互连模型
图2是基于本模型的数据写时序关系图。图中,T0表示主控端内部时钟发生器CLK发出的时钟到达触发器Q1时钟输入端的延时;T1表示触发器Q1接受到时钟后到Q1输出端出现数据的延时;T2表示主控端内部时钟发生器CLK发出的时钟到主控端外部时钟输出引脚的延时;T3表示内部触发器Q1输出的数据到达主控端外部数据输出引脚的延时。通常,半导体制造商不会给出T0-T3这些参数,通常会给出一个用于反映这些参数最终等价效果的参数,即主控端外部数据引脚上出现数据时相对于外部时钟引脚出现时钟信号的延时,这里记为Tco。
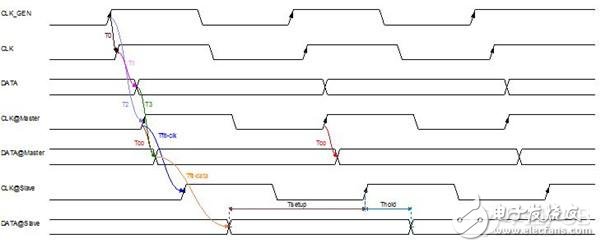
图2 高速电路设计_数据写时序关系图
时序分析最关心的参数是信号到达接受端的最终建立时间和保持时间是否符合器件要求。这里将建立时间和保持时间分别记为Tsetup和Thold。Tflt-clk和Tflt-data分别表示时钟信号和数据信号的飞行时间,即他们在对应走线上的延时。Tjitter-clk和Tjitter-data分别代表时钟信号和数据信号上的抖动时间。
器件的建立时间和保持时间是通过描述器件外部的时钟引脚和数据引脚上的时序关系来反映器件内部相关的时序延时和相关目标逻辑时序关系的集总参数。信号从器件的引脚到内部目标逻辑存在一定延时,同时内部逻辑需要最终的建立和保持时间,综合器件内部的这些需求,最终得到器件对外的时序要求。
分析图2中时钟信号和数据信号的相互关系,可以发现:由于Tco的存在,如果器件间的时钟和数据走线等长,则在接收端,用于发送时间的边沿不能用于数据的采样。为了在接收端对数据进行正确采样,必须调整时钟和数据走线的关系,有两种方法:第一,时钟走线长于数据走线,使得数据飞行时间较时钟短。此时,在接收端仍然可以使用产生数据的时钟沿采样数据;第二,数据走线比时钟长,使得数据飞行时间较时钟长。此时,可以使用使用产生数据时钟沿的下一个上升沿采样数据。
实际工程中,设计人员一般使用第二种方法并希望对于数字系统的建立时间和保持时间都留有一定裕量,因此我们可以得出下列公式,即建立时间公式:
(Tsetup)min + (Tco)max + (Tflt-data - Tflt-clk)max + Tjitter-clk+ Tjitter-data < T (1)
和保持时间公式:
(Tco)min + (Tflt-data - Tflt-clk)min - Tjitter-clk- Tjitter-data > (Thold)min (2)
很显然,Tco、Tflt-data 、Tflt-clk中,Tco是器件的固有参数,Tflt-data 和Tflt-clk取决于对应的PCB走线长度和走线层等。如果Tflt-data 和Tflt-clk的差过小,则导致数据的保持时间不足;如果过大,则会使得建立时间不足。因此,Tflt-data 和Tflt-clk的差存在上限和下限双重限制。

图3 高速电路设计_数据读时序关系图
图3是基于本模型的数据读时序关系图。图中参数含义与前述相同。需要注意的是:在读关系中,时钟首先需要从主控端传到从端,待从端发出的数据回到主控端后,才能由主控端对数据进行采样。因此,建立和保持时间的公式如下:
(Tsetup)min + (Tco)max + (Tflt-data)max + (Tflt-clk)min + Tjitter-clk+ Tjitter-data < T (3)
(Thold)min< (Tco)min + (Tflt-data)min + (Tflt-clk)max - Tjitter-clk- Tjitter-data (4)
参数Tco、Tflt-data 、Tflt-clk中,To是器件的固有参数,Tflt-data 和Tflt-clk取决于对应的PCB走线长度和走线层等。如果Tflt-data 和Tflt-clk的总和过小,则导致数据的保持时间不足;如果过大,则会使得建立时间不足。因此,Tflt-data 和Tflt-clk的和存在上限和下限双重限制。
需要额外说明的是,前述公式的分析中暗含一个结果,就是:默认器件的输出保持时间和输出延时是等时间的。实际上,不同的半导体器件具有不同的情况,即使同一个半导体器件,在每次输出数据时也不一定是完全相同的。这正是本文开始就一再强调的,时序分析的公式并不是万能的,尽管大多数情况均适用,鉴于现实世界中的情况多样,必须具体问题具体分析。
还有一个问题:是否可以使用产生数据时钟沿的次次上升沿采样数据,或者更靠后的边沿来采样数据。图4所示是1#时钟沿发出的数据由3#时钟沿采样的例子,在前述内容中,1#时钟沿发出的数据均由2#时钟沿采样。此处。为了在接收端有较好的建立和保持时间,可以看出数据的飞行时间最好要大于一个时钟周期。假设此时钟周期为40ns,表层走线,板材为FR-4,则数据线的最小长度要635CM。即使时钟周期为8ns,数据线最小长度也要127CM。这显然不是我们所希望的。因此,实际中使用产生数据时钟沿的次上升沿来采样数据。
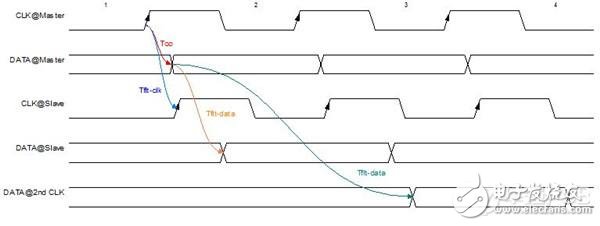
图4 高速电路设计_使用数据产生沿的后续边沿采样数据
2. 时序分析实例
(1) MII接口
MII接口是最常用的百兆以太网PHY芯片与MAC间的接口,表1和表2分别是某百兆PHY芯片和某MPU内部MAC的RX通道时序参数表。

表1 高速电路设计_某PHY芯片RX通道时序参数表
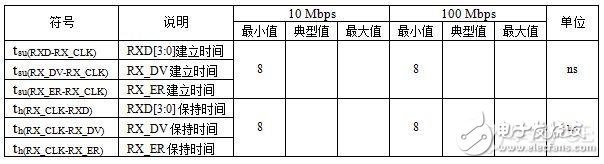
表2 高速电路设计_某MPU内MAC RX通道时序参数表
通过表格可以看出,MAC侧要求RXD、RX_DV和RX_ER信号对RX_CLK信号的建立与保持时间最小为8ns,也就是实际的建立与保持时间不得小于8ns。假设RXD、RX_DV与RX_CLK信号从PHY侧到MAC侧的延时完全相同,则在MAC侧有:
传输的时钟周期为40ns;
最小的建立时间为40-tval =12ns;
最小的保持时间为thold = 10ns;
最小的建立时间和保持时间总和为22ns;
假设RXD、RX_DV和RX_ER信号对RX_CLK信号存在延时,则存在两种极端情况:
当延时导致建立时间达到最低要求,即当相对延时为+4ns时,则在MAC侧建立时间为8ns,保持时间为14ns;
当延时导致保持时间达到最低要求,即当相对延时为-2ns时,则在MAC侧建立时间为14ns,保持时间为8ns;
假设MII接口走线在PCB表层,PCB板材为FR-4,可知信号传输速度大约为160ps/inch,综合上述两种情况,可以得出RXD、RX_DV和 RX_ER相对RX_CLK的走线长度关系为:延迟+4ns时,RXD、RX_DV和RX_ER走线相对RX_CLK可以长:4000/160 * 2.54 = 63CM; 延迟-2ns时,RXD、RX_DV和RX_ER走线相对RX_CLK可以短:2000/160 * 2.54 = 32CM;可见,对于MII的RX通道信号,可以无需考虑等长。
注意,时序关系不代表不需要考虑反射问题。当信号在走线上的传播和返回延时比信号的上升时间长时,就有必要考虑是否进行终端阻抗匹配以抑制反射。
下面使用公式进行计算,以对比理论分析和公式法的优劣。为简化计算,忽略公式(1)和公式(2)中的抖动因素Tjitter-clk和Tjitter-data,相关公式变为:
(Tsetup)min + (Tco)max + (Tflt-data - Tflt-clk)max< T (5)
(Tco)min + (Tflt-data - Tflt-clk)min>(Thold)min (6)
将表2和表3中的参数带入公式(5)和公式(6),得出:
10 - (Tco)minflt-data - Tflt-clk< 4
由于PHY芯片参数并没有给出(Tco)min这个参数,所以公式无法得到最终结果。由于PHY芯片的最长输出延时为28ns,最短保持时间为10ns,在此假设(Tco)min为12ns,则:
-2flt-data - Tflt-clk< 4
可分解为:
Tflt-data - Tflt-clk< 4
Tflt-clk -Tflt-data< 2
换算成长度就是:
Lflt-data - Lflt-clk<63cm< p="">
Lflt-clk -Lflt-data<32cm< p="">
可以看出,使用公式分析时有时会受到参数不全的制约,这时需要根据其他参数推断出需要的参数。对比分析法和公式法,可以看出:分析法比较繁琐,需要认真分析时序关系,而公式法却非常快捷。
不过,公式法有时会受到参数的制约,得不到全面的结论。实际中,应该两种方法结合使用。
下面分析该PHY芯片和MAC间TX通道的时序。表3和表4分别是该百兆PHY芯片和MPU内部MAC的TX通道时序参数表。
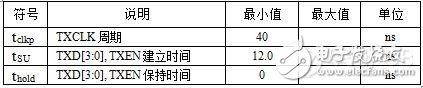
表3 高速电路设计_某PHY芯片TX通道时序参数表

表4 高速电路设计_某MPU内MAC TX通道时序参数表
使用公式进行计算,为简化忽略公式(3)和公式(4)中的抖动因素Tjitter-clk和Tjitter-data,则相关公式变为:
(Tsetup)min + (Tco)max + (Tflt-data)max + (Tflt-clk)min< T
(Thold)min< (Tco)min + (Tflt-data)min + (Tflt-clk)max
带入上述参数表中的参数,化简得到:
Lflt-data + Lflt-clk< 47.625CM
假设MII走线在PCB表层,PCB材料为FR-4,走线传输速度为160ps/inch,综合上述分析,可以得出TXD、 TXEN 分别和 TXCLK的走线之和不能大于47CM。实际布线中,本组走线应当越短越好。走线越短,则数据的建立时间越充足,保持时间越少。本实例中,恰好MAC侧允许保持时间为0ns。
(2)RMII接口
RMII接口也是常用的百兆以太网PHY芯片与MAC间的接口。表5是某百兆PHY的时序参数表,表6和表7分别是某MPU内部MAC的时序参数表。
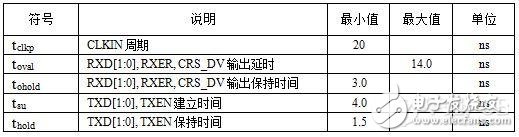
表5 高速电路设计_某PHY芯片的时序参数表
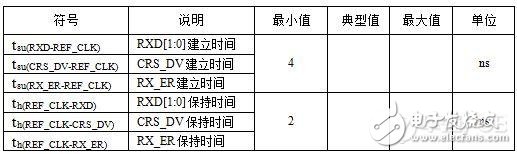
表6 高速电路设计_某MPU内MAC RX通道时序参数表

表7 高速电路设计_某MPU内MAC TX通道时序参数表
该MPU内MAC在RMII模式时,不支持时钟输出,同时PHY要求时钟信号为输入。该MPU配合PHY工作在RMII模式下,需要外部使用一颗符合双方精度要求的50MHz振荡器,来为双方提供时钟基准。
为简化时序分析,可以将外部振荡器至MPU和PHY双方的走线设计为等长,此时时钟信号在两者的时钟输入引脚上具有完全一致的时刻。
注意:等长走线的一般实现方法是蛇形线,但等长的蛇形线并不一定意味着等延时。只有当蛇形线的延时效果等同或者尽可能近似于直线时,等长才意味着等延时。为了让蛇形线具有类似于直线的延时效果,蛇形线的高度应尽可能小,蛇形线的开口应尽可能宽,也就是说,波浪线的外形更利于等延时。
当时钟信号等时刻到达收发双方的输入引脚时,具有如图5所示的时序模型,因而仅需讨论数据线的长度。
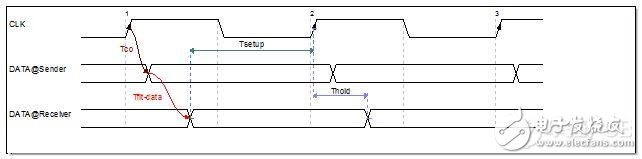
图5 高速电路设计_共用时钟的RMII时序模型
根据上述时序模型,可得出下列时序公式:
(Tsetup)min + (Tco)max + (Tflt-data)max + Tjitter-clk+ Tjitter-data < T (7)
(Tco)min + (Tflt-data)min - Tjitter-clk- Tjitter-data >(Thold)min (8)
对RXD、CRS_DV和RX_ER信号来说,该组信号由PHY发给MPU,根据公式(7)和公式(8),可得(为了简化,认为最小的Tco时间等于Thold时间):
-1 flt-data < 2
走线时间不可能为负值,假设走线位于PCB表层,材料为FR-4,则:
Lflt-data < 31.75CM
对TXD、和TX_EN信号来说,该组信号由MPU发给PHY,根据公式(7)和公式(8),可得:
-0.5 flt-data < 3
走线时间不可能为负值,假设走线位于PCB表层,材料为FR-4,则:
Lflt-data < 47.625CM
对 RXD、CRS_DV和RX_ER信号来说,该组信号由PHY发给MPU。假设数据线走线长度为0,则数据线延时为0ns,此时在MPU侧接受到信号的最小建立时间为:20-14=6ns,最小保持时间为:3ns。MAC侧要求的最小建立时间为4ns,最小保持时间为2ns。可见,此时数据线的走线长度最长延时可以到2ns,此时MAC侧接受到信号的建立时间和保持时间分别为4ns和5ns,符合时序要求。所以走线长度最长可以为31.75CM。
对 TXD和TX_EN信号来说,该组信号由MPU发给PHY。假设数据线走线长度为0,则数据线延时为0ns,此时在PHY侧接受到信号的最小建立时间为:20-13=7ns,最小保持时间为:2ns。MAC侧要求的最小建立时间为4ns,最小保持时间为1.5ns。可见,此时数据线的走线长度最长延时可以到3ns,此时MAC侧接受到信号的建立时间和保持时间分别为4ns和4.5ns,符合时序要求。所以走线长度最长可以为47.625CM。
(3)RGMII接口
RGMII接口是最常用的千兆以太网PHY芯片与MAC间的接口,表8和表9分别是某千兆PHY芯片和某MPU内部千兆MAC的TX通道时序参数表。该千兆MAC不支持RGMII-ID功能,为简化布线工作,PHY内部双向启用 RGMII-ID功能,相关时序参数为RGMII-ID功能使能后的数值。注意,RGMII时序为DDR模式。
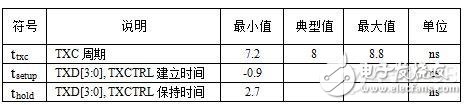
表8 高速电路设计_某千兆PHY芯片 TX通道时序参数表

表9 高速电路设计_某MPU内千兆MAC TX通道时序参数表
本组数据由MAC发往PHY,为源时钟同步。在PHY端开启内部延时的情况下,要求接受数据的建立时间和保持时间最小值分别为-0.9ns和2.7ns。最差情况下,MPU端发送数据的最小建立时间为-0.5ns,最小保持时间为4-0.5=3.5ns。因此,时钟线和数据线等长是最简单的布线方法。
假设数据信号相对时钟信号存在正延时,为了保证PHY端最小的建立时间-0.9ns,数据最多可以相对时钟延时+0.4ns。最差情况下,有:
PHY侧数据相对时钟的延时为-0.9ns,即建立时间为-0.9ns;
由于数据独立存在期不会低于4-0.5-0.5=3ns,因此保持时间永远不低于3.5ns;
此时,系统整体满足时序要求,数据线可以比时钟线长6.35CM。
假设数据信号相对时钟信号存在负延时,为了保证PHY端最小的保持时间2.7ns,由于数据相对于时钟边沿的存在期不短于3.5ns,设数据最多可以相对时钟延时-0.8ns。最差情况下,有:
PHY侧数据相对时钟的延时为0.3ns,即建立时间为0.3ns;
PHY侧数据的保持时间为3.5-0.8=2.7ns;
此时,系统整体满足时序要求,时钟线可以比数据线长12.7CM。
表10和表11分别是该千兆PHY芯片和该MPU内部千兆MAC的TX通道时序参数表。本组时序分析较为简单,很容易分析出数据走线对时钟走线的延时偏差可以为±0.2ns,对于表层走线,FR-4材料,折算成走线长度就是3.175CM。

表10 高速电路设计_某千兆PHY芯片 TX通道时序参数表
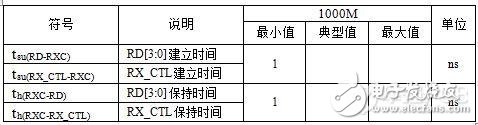
表11 高速电路设计_某MPU内千兆MAC TX通道时序参数表
图6是RGMII的时序模型,即DDR模式的时序图。公式(9)和公式(10)是对应的建立时间和保持时间约束公式。公式中, Tstrobe – data表示选通信号相对数据信号的传送延时;Tdata -strobe表示数据信号相对选通信号的传送延时。
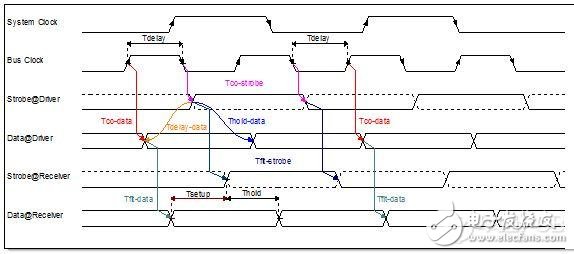
图6 高速电路设计_RGMII时序模型图
(Tsetup)min< (Tco)min +( Tstrobe - data )min – Tjitter-data – Tjitter-strobe (9)
(Thold)min< (Thold-data)min + (Tdata -strobe)min – Tjitter-data – Tjitter-strobe (10)
将RGMII时序参数表中的相应参数带入公式(9)和(10),可得:
对于RX通道:
Tdata-strobe< 0.4
Tstrobe–data < 0.8
即相当于:
Ldata-Lstrobe< 6.35CM
或
Lstrobe–Ldata< 12.7CM
可见,公式计算结果与理论分析结果一致。TX通道可使用类似方法计算。
(4)SPI接口
出于成本因素,越来越多的消费电子使用SPI FLASH作为存储器。SPI的通信速度也越来越高。目前,多数MPU都可以支持100M以上的SPI通信速度且支持多I/O通信。
SPI通信的时序关系与前述有所不同,图7和图8分别是SPI在模式1下的数据读时序和数据写时序,公式(11)、公式(12)、公式(13)和公式(14)是对应的时序约束公式。可以看出,由于时序关系的不同,公式也会有所变化。所以,时序分析要具体问题具体对待。
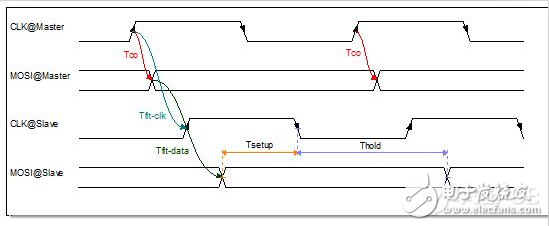
图7 高速电路设计_SPI模式1的写时序

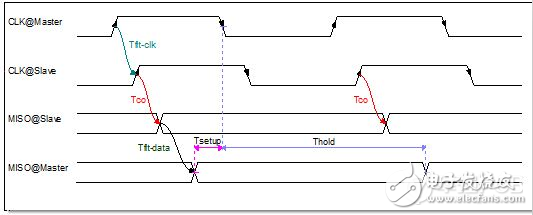
图8 高速电路设计_SPI模式1的读时序

3. 结论
进行时序分析的关键点首先在于必须对被分析的时序关系非常清楚、能够深刻理解当前对象的时序协议。其次,时序分析要针对具体问题具体分析,不存在所谓的万能时序公式。有时,单纯依靠理论分析或者单纯依靠时序关系公式并不一定能够解决问题,而是要两者结合使用。
对于高速信号的布线而言,存在“等长”说,即很多工程师认为只要所有的线路尽可能等长,就一定满足时序要求。事实上,这是一种错误的认识,本文的实例分析就明确证明了这一点。只有那些时钟和数据由同一个器件发出,由另一个器件接受,并且发送端的建立时间和保持时间恰好满足接收端需求时,“等长”才算是一种偷懒的方法。除此以外,尤其是那些通过单向时钟驱动、采样双向数据或者逆向数据的信号,必须具体问题具体分析。当然,对于PC机这类通用设备来说,由于主板的设计需要兼容不同厂家的内存条,此时走线设计为等长确实是合理的设计。
公共时钟系统由于使用单向时钟信号对双向数据进行采样,因此存在双重限制,两组限制制约了走线不仅有走线长度差值限制,同时还有走线总长度限制。源同步时钟系统使用与数据同向的时钟,因此只存在单重限制,使得走线只有差限制而没有总长度限制。
一般而言,对于SPI接口、MII接口、共享时钟的RMII接口或者SDRAM信号,走线应尽可能的短。对于DDR SDRAM信号以及RGMII等DDR时序的接口来说,多数情况下,组内等长确实是一种简便快速的方法。
 电子发烧友App
电子发烧友App






















评论