互联网络培训教程[1]
学习目标:
掌握互连网络的定义、性能参数。
掌握互连函数的概念。
掌握几种数据路由功能的含义和特点。(循环、置换、均匀混洗 、超立方体路由功能、广播、选播)
掌握静态网络的拓扑结构及特点。(线性阵列、环和带弦环、全连接网络、循环移数网络、树形和星形、胖树形、网格形和环网、超立方体、k元n-立方体网络)
掌握动态网络的分类方法和动态网络的拓扑结构。 (总线系统、交叉开关网络 、多端口存储器、多级网络)
正文:
6.3互联网络
互连网络是将集中式系统或分布式系统中的结点连接起来所构成的网络,这些结点可能是处理器、存储模块或者其他设备,它们通过互连网络进行信息交换。在拓扑上,互连网络为输入和输出两组结点之间提供一组互连或映象(mapping)。
本节介绍构造多处理机的互连网络。首先讨论互连网络的通信特性和拓扑结构,然后再来分析并行结构的可扩展性。我们希望得到的是数据传送速率高、延迟低、通信频带宽的网络。
6.3.1互联网络的性能参数
互连网络的拓扑可以采用静态或动态的结构。
1. 静态网络由点和点直接相连而成,这种连接方式在程序执行过程中不会改变。静态网络常用来实现一个系统中子系统或计算结点之间的固定连接。
2. 动态网络是用开关通道实现的,它可动态地改变结构,使其与用户程序中的通信要求匹配。
动态网络常用于集中式共享存储器多处理系统中。
下面定义几个常用于估算网络复杂性、通信效率和价格的参数。
(1) 网络规模
一般说来,网络用图来表示。这种图由用有向边或无向边连接的有限个结点构成。其结点数称为网络规模(network size)。
(2) 结点度
与结点相连接的边的数目称为结点度(node degree)。这里的边表示链路或通道。链路或通道是指网络中连接两个结点并传送数字信号的通路。在单向通道的情况下,进入结点的通道数叫做入度(in degree),而从结点出来的通道数则称为出度(out degree),结点度是这两者之和。结点度应尽可能地小并保持恒定。
(3) 网络直径
网络中任意两个结点间最短路径长度的最大值称为网络直径。网络直径应当尽可能地小。
(4) 等分宽度
在将某一网络切成相等两半的各种切法中,沿切口的最小通道边数称为通道等分宽度(channel bisection width)。等分宽度是能很好地说明将网络等分的交界处最大通信带宽的一个参数另一个量化参数是结点间的线长(或通道长度)。它会影响信号的延迟、时钟扭斜和对功率的需要。对于一个网络,如果从其中的任何一个结点看,拓扑结构都是一样的话,则称此网络为对称网络。对称网络较易实现,编制程序也较容易。
(5) 路由(routing)
在网络通信中对路径的选择与指定。互连网络中路由功能较强将有利于减少数据交换所需的时间,因而能显著地改善系统的性能。通常见到的处理单元之间的数据路由功能有移数、循环、置换(一对一)、广播(一对全体)、选播(多对多)、个人通信(一对多)、混洗、交换等。这些路由功能可在环形、网络形、超立方体以及多级网络上实现。
为了反映不同互连网络的连接特性,每一种互连网络可用一组互连函数来定义。如果把互连网络的N个入端和N个出端各自用整数0,1,…,N-1代表,则互连函数表示互连的出端号和入端号的一一对应关系。令互连函数为f,则它的作用是:对于所有的0≤j≤N-1, 同时存在入端j连至出端f(j)的对应关系。
下面介绍几种数据路由功能:
1. 循环(rotation)
若把互连函数f(x)表示为:
(x0,x1,x2,……,xj)
则代表对应关系为:
f(x0)=x1,f(x1)=x2,……,f(xj)=x0
j+1称为该循环的周期。
2. 置换(permutation)
指对象的重新排序。对于n个对象来说,有n!种置换。n个对象可照此重新排序,全部的置换形成一个与复合运算有关的置换集合。例如,置换π=(a,b,c)(d,e)表示了置换映射:f(a)=b,f(b)=c,f(c)=a,f(d)=e和f(e)=d。这里循环(a,b,c)周期为3,循环(d,e)周期为2。可以用交叉开关来实现置换,也可以用一次或多次通过多级网络来实现某些置换,还可用移数或广播操作实现置换。
3. 均匀混洗(shuffle)
n=8(对象个数)的均匀混洗所对应的映射如图6.3.1所示,图6.3.2为其逆过程。
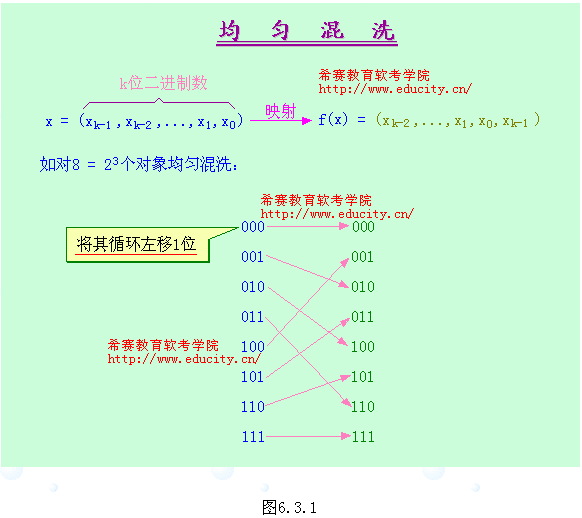
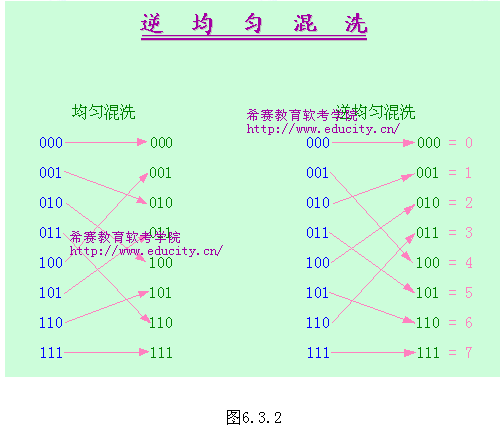
一般说来,为了对n=2k个对象均匀混洗,我们可用k位二进制数x=(xk-1,…,x1,x0)来表示定义域中的每个对象。均匀混洗将x映射到f(x),得到f(x)=( xk-2,…,x1,x0,xk-1)。这是将x循环左移1位得到。
4.超立方体路由功能
图6.3.3表示的是一个三维二进制立方体网络。它有三种路由功能,可分别根据结点的二进制地址(C2 C1 C0)中的某一位来确定。例如,可以根据最低位C0寻址,即在最低位C0不同的相邻结点之间交换数据,如图6.3.4所示。同样,分别根据中间位C1 (图6.3.5)和最高位C2 (图6.3.6)可得其它两种路由模式。
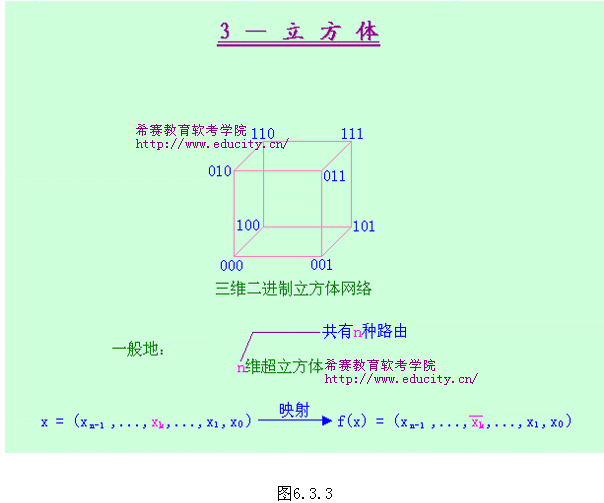
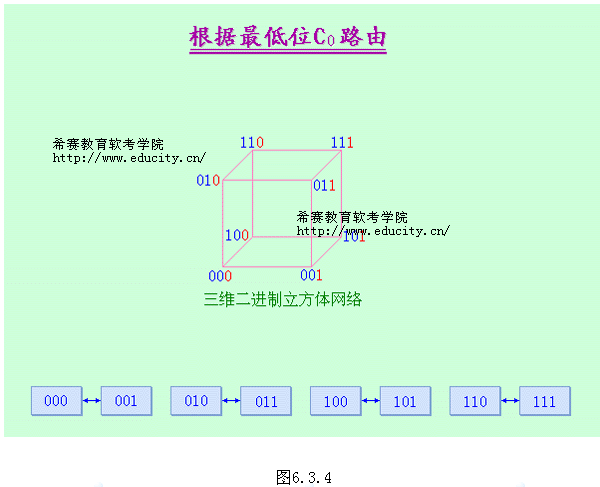

一般情况下,一个n维超立方体共有n种路由功能,分别由n位地址中的每一位求反位值来确定。将x=(xn-1,…,x1,x0)映射到f(x),得到f(x)=( xn-1, …, xk,…,x1,x0)。
非常好我支持^.^
(1) 100%
不好我反对
(0) 0%
相关阅读:
- [电子说] SIT1024Q四通道本地互联网络(LIN)物理层收发器 2023-08-11
- [今日头条] SIT1029Q 带显性超时,本地互联网络(LIN)收发器 2023-08-07
- [电子说] SIT1021Q 本地互联网络(LIN)收发器 2023-08-07
- [电子说] 四通道本地互联网络(LIN)收发器SIT1024Q 2023-08-14
- [电子说] 芯力特四通道本地互联网络LIN收发器--SIT1024Q 2022-12-06
- [电子说] 芯力特双通道本地互联网络LIN收发器--SIT1022Q 2022-11-08
- [电子说] 芯力特四通道本地互联网络LIN收发器SIT1024Q的引脚和特点分析 2022-12-05
- [电子说] 双通道本地互联网络LIN收发器SIT1022Q的引脚与特点分析 2022-11-07
( 发表人:admin )
