在大多数情况下,开关电源(SMPS)反馈环路通过观测特定点上的电压来进行稳压,而其余输出电压则依靠变压器的性能来确保正常运行。在这种情况下,稳定性分析必须包含所有次级元件,以涵盖所有可能的负载配置。毋庸置疑,涵盖所有可能的输入/输出情况的传统分析方法难度高且耗时长,简化分析也容易出错。本文将介绍采用SPICE仿真器进行多输出电源稳定性分析的简化方法。

简单的反射
电阻连接到变压器次级端时,初级端可以“看到”一个等效电阻,如图1所示,其中匝数比在初级归一化。归一化表示将所有比例除以初级匝数比:Np:Ns=10:5,在归一化之后表示为1:0.5。
若变压器性能卓越(Imag=0),则可得出:
1 x I1=N2 x I(方程1),且V2=V1 x N2(方程2)或V1 / V2=1 / N2(方程3)。
因为I2=V2 / RL(方程4),可将方程4代入方程1,得出:
I1=V1 / Req=N2 x V2 / RL(方程5)。重新排列该方程得出:Req=V1 x RL / N2 x V2(方程6)。
根据方程3,最后得到:Req=RL / N22(方程7)。
在这种情况下,变压器变成绕组,简化了分析。
首先用方程7将RL2反射到初级端:Req1=RL2 / N32(方程8)。那么,逆方向应用方程7,将Req1“推至”RL1上:Req2=Req1 x N22=RL2 x N22 / N32。最后,可以得出Req的计算方程:Req=RL1 // [ RL2 x (N2/N3)2 ](方程9)。
除了电阻以外,还可以反射为—简单的电容。在这种情况下,对于正弦波激励,电容阻抗为Zc=1 / j x C x (方程10),此时仍可采用方程7:Ceq=1 / j x C x x N22或Ceq=C x N22(方程11)。
在图2a中,将阻抗反射到另一个绕组。采用方程10和7,可以得出Ceq=(1 / j x C x ) x [N2/N3]2或Ceq=C x [N3 / N2]2(方程12)。注意,该方程与方程9互逆。
如果根据上述结论讨论阻抗,给定阻抗反射到初级端的结果可利用下列方程进行计算:
Zeq=Zload x (N1/N2)2(方程12b)假设N1=1,那么对于电阻,Zeq=Rload x (1/N2)2(方程12c)。对于电容,Zeq=1 / (2 x x f x Cload x N22)(方程12d)。对于电感,Zeq=2 x x f x Lload / N22(方程12e)。
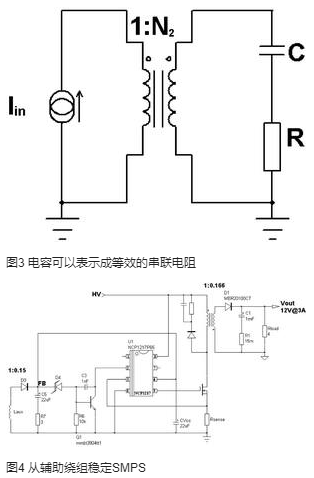
电容始终与等效的串联电阻(ESR)相连,如图3所示。电容C和电阻R串联起来可得到复导纳Y,计算方程为:
Y=或(方程13)。若网络时间常数=R x C,则其阻抗(方程14)。如果采用方程7,则初级端的等效阻抗为:
(方程15)。
当两个受到各自ESR影响的电容并联时,就会产生复阻抗并联现象。然而,通过这种元件组合得到的总阻抗没有简单的表达式。阻抗并联时的导纳表达式为:
1. 假设 R1 x C1=R2 x C2
设Y1是R1.C1的导纳,而Y2是R2.C2的导纳。因此,Ytot=Y1+Y2
Ytot==
=(方程16)。采用方程13中的符号,方程16可以改写为:Ytot=。如果1=2=,那么最后的导纳可简化为:Ytot= (方程17),它与方程13相似,方程13中电容C是两个电容的和(和并联一样),且ESR的值若与(C1+C2)结合,则可得出1或2的值。电阻Req=1 / (C1 + C2),可以从中推出Req=R1 // R2(因为若F→埃?蛄礁龅缛荻冀?搪 )。
因此,并联两个时间常数相同的串联RC网络R1-C1和 R2-C2时,产生的等效串联RC网络由C=C1+C2和R=R1 // R2组成。
2.假设R1 x C1≠R2 x C2
根据方程16,简化表达式中的p并且忽略其中的1后得出:
Ytot=(方程18),与方程13明显不同。
总之,时间常数不同的两个并联RC网络不能简化成一个RC网络。
将反射应用于初级稳压电源
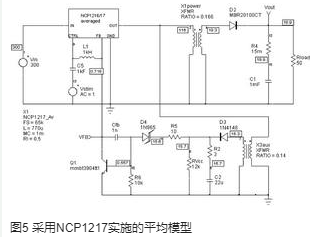
在初级稳压电源应用中,辅助绕组不仅提供控制器的电源Vcc,还提供输出电压的镜象。若两个绕组之间的耦合质量良好,则电平相互之间的追踪便能取得良好的效果。图4为采用NCP1217设计的反击电源。用齐纳二极管和低成本的双极型元件Q1确保反馈。由于反馈电平必须降低以减少功耗,因此该晶体管是必需的。稳压点实际上是D4的阳极、电路Vcc引脚载入的FB点。首先应将所有次级元件反射到初级端,将转换器简化为单个输出的版本。请注意:负载和控制器功耗一起反射,如同电阻在FB点上工作,而且在反射过程中,认为D1和D3的动态电阻接近零。
反射步骤为:
1. 将4负载反射到辅助绕组:4×(0.15 / 0.166)2=3.26
2. 将输出电容反射到辅助绕组:1×(0.166 / 0.15)2=1.22mF
3. 用简单的电阻增加芯片功耗:12V/1mA=12k
4. 由于电容和ESR的时间常数接近,因此可以将两者合并。
在最后的反射上可以定位典型极点和零点,这两点位于在非连续导电模式(DCM)中工作的反击转换器中。
注意:Rload可以用更简单的方法推出。匝数比已知时,12V输出的反馈电压为12×(0.15/0.166)= 10.84V。若在输出上提供3A电流,则功率为36W。从辅助/FB电平来看,其等效负载为P=U2/R或 Req=10.842 / 36=3.26。
SPICE适用于很多情况
一般的SPICE模型使SMPS的稳定性测试变得很简单。测试时无需反射电容、负载、电阻等,也无需调整并联组合:这一切都由SPICE自动完成。在本文的实例中,需要收集反击段模型(电流或电压模式),然后用原理图完成变压器配置。图4的仿真电路如图5所示。
通过在输出上安装开关并且逐步将它载入的方法,可以检查电源的稳定性。此外还可以比较周期间仿真的结果以验证该平均配置。
电路上的功率MOSFET被行为级开关代替,以加速仿真时间。通过观测开关启动时的输出电压,可以比较平均模型和周期间应用的瞬态响应。
结语
本文分析了对开关模式转换器(包括寄生元件,如输出二极管的动态电阻)进行综合稳定性分析的重要性。若不进行分析,在预测极点和零点位置时将产生较大误差。随着转换器日益复杂(如增加次级电感滤波器),传统的手工分析变得极为复杂。而SPICE提供了分析所需的灵活性,同时考虑到反射和动态电阻,使工程师可像处理真实电路一样设置仿真模板,并且顺利地进行AC分析。
责任编辑:gt
 电子发烧友App
电子发烧友App























评论